hdu-1757 A Simple Math Problem---矩阵快速幂模板题

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=1757

题目大意：

求递推式第k项模m

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .

解题思路：

构建矩阵

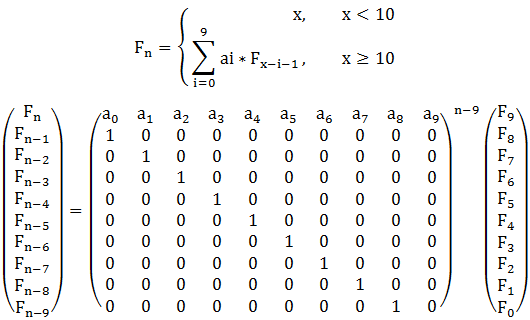
直接用矩阵快速幂模板求解

注意，小于10的时候不能直接输出k，要输出k%m

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100 + 10;
int MOD;
struct Mat
{
    int a[maxn][maxn];
    int n, m;//n为行数，m为列数
    Mat(int n, int m):n(n), m(m)
    {
        memset(a, 0, sizeof(a));
    }
    void init()
    {
        for(int i = 0; i < n; i++)a[i][i] = 1;//初始化成单位矩阵
    }
    void output()
    {
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < m; j++)
            {
                cout<<a[i][j]<<" ";
            }
            cout<<endl;
        }
    }
};
Mat mul(Mat a, Mat b)//矩阵乘法
{
    Mat tmp(a.n, b.m);//矩阵乘法结果矩阵行数为a的行数，列数为b的列数
    for(int i = 0; i < a.n; i++)
    {
        for(int j = 0; j < b.m; j++)
        {
            for(int k = 0; k < a.m; k++)//a.m == b.n(乘法的前提条件)
            {
                tmp.a[i][j] += (a.a[i][k] * b.a[k][j] % MOD);
                tmp.a[i][j] %= MOD;
            }
        }
    }
    return tmp;
}
Mat pow(Mat a, int n)
{
    Mat tmp(a.n, a.m);
    tmp.init();
    while(n)
    {
        if(n & 1)tmp = mul(tmp, a);
        n /= 2;
        a = mul(a, a);
    }
    return tmp;
}
int main()
{
    int n, m;
    while(cin >> n >> m)
    {
        Mat a(10, 10);
        Mat b(10, 1);
        //对a和b进行初始化
        for(int i = 0; i < 10; i++)cin >> a.a[0][i];
        for(int i = 1; i < 10; i++)a.a[i][i - 1] = 1;
        for(int i = 0; i < 10; i++)b.a[i][0] = 9 - i;
        MOD = m;
        //a.output();
        //b.output();
        if(n < 10)
        {
            cout<<(n % m)<<endl;
        }
        else
        {
            Mat ans = pow(a, n - 9);
            //ans.output();
            ans = mul(ans, b);
            cout<<ans.a[0][0]<<endl;
        }
    }
}