KM算法（运用篇）

传送门：KM算法---理解篇

最佳匹配

什么是完美匹配

如果一个二分图，X部和Y部的顶点数相等，若存在一个匹配包含X部与Y部的所有顶点，则称为完美匹配。
换句话说：若二分图X部的每一个顶点都与Y中的一个顶点匹配，**并且**Y部中的每一个顶点也与X部中的一个顶点匹配，则该匹配为完美匹配。

什么是完备匹配

如果一个二分图，X部中的每一个顶点都与Y部中的一个顶点匹配，**或者**Y部中的每一个顶点也与X部中的一个顶点匹配，则该匹配为完备匹配。

什么是最佳匹配

带权二分图的权值最大的完备匹配称为最佳匹配。

二分图的最佳匹配不一定是二分图的最大权匹配。

转化

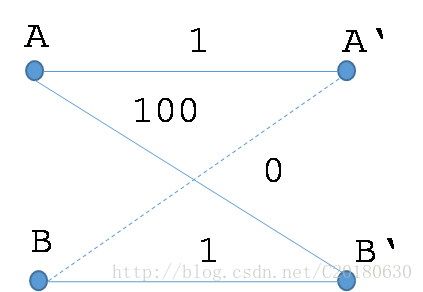
可以添加一些权值为0的边，使得最佳匹配和最大权匹配统一起来。

KM算法

求二分图的最佳匹配有一个非常优秀的算法,可以做到O(N^3),这就是KM算法。该算法描述如下：

1.首先选择顶点数较少的为X部，初始时对X部的每一个顶点设置顶标，顶标的值为该点关联的最大边的权值，Y部的顶点顶标为0。

2.对于X部中的每个顶点，在相等子图中利用匈牙利算法找一条增广路径，如果没有找到，则修改顶标，扩大相等子图，继续找增广路径。当每个点都找到增广路径时，此时意味着每个点都在匹配中，即找到了二分图的完备匹配。该完备匹配即为二分图的最佳匹配。

什么是相等子图呢？因为每个顶点有一个顶标，如果我们选择边权等于两端点的顶标之和的边，它们组成的图称为相等子图。

如果从X部中的某个点Xi出发在相等子图中没有找到增广路径，我们是如何修改顶标的呢？如果我们没有找到增广路径，则我们一定找到了许多条从Xi出发并结束于X部的匹配边与未匹配边交替出现的路径，姑且称之为交错树。我们将交错树中X部的顶点顶标减去一个值d，交错树中属于Y部的顶点顶标加上一个值d。这个值后面要讲它如何计算。那么我们会发现：

两端都在交错树中的边(i,j)，其顶标和没有变化。也就是说，它原来属于相等子图，现在仍属于相等子图。
两端都不在交错树中的边(i,j)，其顶标也没有变化。也就是说，它原来属于（或不属于）相等子图，现在仍属于（或不属于）相等子图。
X端不在交错树中，Y端在交错树中的边(i,j)，它的顶标和会增大。它原来不属于相等子图，现在仍不属于相等子图。
X端在交错树中，Y端不在交错树中的边(i,j),它的顶标和会减小。也就说，它原来不属于相等子图，现在可能进入了相等子图，因而使相等子图得到了扩大。
我们修改顶标的目的就是要扩大相等子图。为了保证至少有一条边进入相等子图，我们可以在交错树的边中寻找顶标和与边权之差最小的边,这就是前面说的d值。将交错树中属于X部的顶点减去d，交错树中属于Y部的顶点加上d。则可以保证至少有一条边扩充进入相等子图。

3.当X部的所有顶点都找到了增广路径后，则找到了完备匹配，此完备匹配即为最佳匹配。

相等子图的若干性质

在任意时刻，相等子图上的最大权匹配一定小于等于相等子图的顶标和。
在任意时刻，相等子图的顶标和即为所有顶点的顶标和。
扩充相等子图后，相等子图的顶标和将会减小。
当相等子图的最大匹配为原图的完备匹配时，匹配边的权值和等于所有顶点的顶标和，此匹配即为最佳匹配

以上就是KM算法的基本思路。但是朴素的实现方法，时间复杂度为O(n4)——需要找O(n)次增广路，每次增广最多需要修改O(n)次顶标，每次修改顶标时由于要枚举边来求d值，复杂度为O(n2)。实际上KM算法的复杂度是可以做到O(n3)的。我们给每个Y顶点一个“松弛量”函数slack，每次开始找增广路时初始化为无穷大。在寻找增广路的过程中，检查边(i,j)时，如果它不在相等子图中，则让slack[j]变成原值与 A[i]+B[j]-w[i,j]的较小值。这样，在修改顶标时，取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点：修改顶标后，要把所有不在交错树中的Y顶点的slack值都减去d

模板一，用全局变量minz表示边权和顶标最小的差值，省去slack数组

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<vector>
 5 #include<map>
 6 using namespace std;
 7 typedef long long ll;
 8 const int maxn = 300 + 10;
 9 const int INF = 0x3f3f3f3f;
10 
11 int wx[maxn], wy[maxn];//每个点的顶标值（需要根据二分图处理出来）
12 int cx[maxn], cy[maxn];//每个点所匹配的点
13 int visx[maxn], visy[maxn];//每个点是否加入增广路
14 int cntx, cnty;//分别是X和Y的点数
15 int Map[maxn][maxn];//二分图边的权值
16 int minz;//边权和顶标最小的差值
17 
18 bool dfs(int u)//进入DFS的都是X部的点
19 {
20     visx[u] = 1;//标记进入增广路
21     for(int v = 1; v <= cnty; v++)
22     {
23         if(!visy[v] && Map[u][v] != INF)//如果Y部的点还没进入增广路,并且存在路径
24         {
25             int t = wx[u] + wy[v] - Map[u][v];
26             if(t == 0)//t为0说明是相等子图
27             {
28                 visy[v] = 1;//加入增广路
29 
30                 //如果Y部的点还未进行匹配
31                 //或者已经进行了匹配，可以从原来的匹配反向找到增广路
32                 //那就可以进行匹配
33                 if(cy[v] == -1 || dfs(cy[v]))
34                 {
35                     cx[u] = v;
36                     cy[v] = u;//进行匹配
37                     return 1;
38                 }
39             }
40             else if(t > 0)//此处t一定是大于0，因为顶标之和一定>=边权
41             {
42                 minz = min(minz, t);//边权和顶标最小的差值
43             }
44         }
45     }
46     return false;
47 }
48 
49 int KM()
50 {
51     memset(cx, -1, sizeof(cx));
52     memset(cy, -1, sizeof(cy));
53     memset(wx, 0, sizeof(wx));//wx的顶标为该点连接的边的最大权值
54     memset(wy, 0, sizeof(wy));//wy的顶标为0
55     for(int i = 1; i <= cntx; i++)//预处理出顶标值
56     {
57         for(int j = 1; j <= cnty; j++)
58         {
59             if(Map[i][j] == INF)continue;
60             wx[i] = max(wx[i], Map[i][j]);
61         }
62     }
63     for(int i = 1; i <= cntx; i++)//枚举X部的点
64     {
65         while(1)
66         {
67             minz = INF;
68             memset(visx, 0, sizeof(visx));
69             memset(visy, 0, sizeof(visy));
70             if(dfs(i))break;//已经匹配正确
71 
72             //还未匹配，将X部的顶标减去minz，Y部的顶标加上minz
73             for(int j = 1; j <= cntx; j++)
74                 if(visx[j])wx[j] -= minz;
75             for(int j = 1; j <= cnty; j++)
76                 if(visy[j])wy[j] += minz;
77         }
78     }
79 
80     int ans = 0;//二分图最优匹配权值
81     for(int i = 1; i <= cntx; i++)
82         if(cx[i] != -1)ans += Map[i][cx[i]];
83     return ans;
84 }
85 int n, k;
86 int main()
87 {
88     while(scanf("%d", &n) != EOF)
89     {
90         for(int i = 1; i <= n; i++)
91         {
92             for(int j = 1; j <= n; j++)
93                 scanf("%d", &Map[i][j]);
94         }
95         cntx = cnty = n;
96         printf("%d\n", KM());
97     }
98     return 0;
99 }

模板二，用slack数组（对于完全图的优化很快）

和全局变量不同的是，全局变量在每次while循环中都需要赋值成INF，每次求出的是所有点的最小值，而slack数组在每个while外面就初始化好，每次while循环slack数组的每个值都在用到，一次增广路中求出的slack值会更准确，循环次数比全局变量更少

  1 #include<iostream>
  2 #include<cstring>
  3 #include<cstdio>
  4 #include<vector>
  5 #include<map>
  6 using namespace std;
  7 typedef long long ll;
  8 const int maxn = 300 + 10;
  9 const int INF = 0x3f3f3f3f;
 10 
 11 int wx[maxn], wy[maxn];//每个点的顶标值（需要根据二分图处理出来）
 12 int cx[maxn], cy[maxn];//每个点所匹配的点
 13 int visx[maxn], visy[maxn];//每个点是否加入增广路
 14 int cntx, cnty;//分别是X和Y的点数
 15 int Map[maxn][maxn];//二分图边的权值
 16 int slack[maxn];//边权和顶标最小的差值
 17 
 18 bool dfs(int u)//进入DFS的都是X部的点
 19 {
 20     visx[u] = 1;//标记进入增广路
 21     for(int v = 1; v <= cnty; v++)
 22     {
 23         if(!visy[v] && Map[u][v] != INF)//如果Y部的点还没进入增广路,并且存在路径
 24         {
 25             int t = wx[u] + wy[v] - Map[u][v];
 26             if(t == 0)//t为0说明是相等子图
 27             {
 28                 visy[v] = 1;//加入增广路
 29 
 30                 //如果Y部的点还未进行匹配
 31                 //或者已经进行了匹配，可以从原来的匹配反向找到增广路
 32                 //那就可以进行匹配
 33                 if(cy[v] == -1 || dfs(cy[v]))
 34                 {
 35                     cx[u] = v;
 36                     cy[v] = u;//进行匹配
 37                     return 1;
 38                 }
 39             }
 40             else if(t > 0)//此处t一定是大于0，因为顶标之和一定>=边权
 41             {
 42                 slack[v] = min(slack[v], t);
 43                 //slack[v]存的是Y部的点需要变成相等子图顶标值最小增加多少
 44             }
 45         }
 46     }
 47     return false;
 48 }
 49 
 50 int KM()
 51 {
 52     memset(cx, -1, sizeof(cx));
 53     memset(cy, -1, sizeof(cy));
 54     memset(wx, 0, sizeof(wx));//wx的顶标为该点连接的边的最大权值
 55     memset(wy, 0, sizeof(wy));//wy的顶标为0
 56     for(int i = 1; i <= cntx; i++)//预处理出顶标值
 57     {
 58         for(int j = 1; j <= cnty; j++)
 59         {
 60             if(Map[i][j] == INF)continue;
 61             wx[i] = max(wx[i], Map[i][j]);
 62         }
 63     }
 64     for(int i = 1; i <= cntx; i++)//枚举X部的点
 65     {
 66         memset(slack, INF, sizeof(slack));
 67         while(1)
 68         {
 69 
 70             memset(visx, 0, sizeof(visx));
 71             memset(visy, 0, sizeof(visy));
 72             if(dfs(i))break;//已经匹配正确
 73             
 74             
 75             int minz = INF;
 76             for(int j = 1; j <= cnty; j++)
 77                 if(!visy[j] && minz > slack[j])
 78                     //找出还没经过的点中，需要变成相等子图的最小额外增加的顶标值
 79                     minz = slack[j];
 80             //和全局变量不同的是，全局变量在每次while循环中都需要赋值成INF，每次求出的是所有点的最小值
 81             //而slack数组在每个while外面就初始化好，每次while循环slack数组的每个值都在用到
 82             //在一次增广路中求出的slack值会更准确，循环次数比全局变量更少
 83             
 84                 
 85             //还未匹配，将X部的顶标减去minz，Y部的顶标加上minz
 86             for(int j = 1; j <= cntx; j++)
 87                 if(visx[j])wx[j] -= minz;
 88             for(int j = 1; j <= cnty; j++)
 89                 //修改顶标后，要把所有不在交错树中的Y顶点的slack值都减去minz
 90                 if(visy[j])wy[j] += minz;
 91                 else slack[j] -= minz;
 92         }
 93     }
 94 
 95     int ans = 0;//二分图最优匹配权值
 96     for(int i = 1; i <= cntx; i++)
 97         if(cx[i] != -1)ans += Map[i][cx[i]];
 98     return ans;
 99 }
100 int n, k;
101 int main()
102 {
103     while(scanf("%d", &n) != EOF)
104     {
105         for(int i = 1; i <= n; i++)
106         {
107             for(int j = 1; j <= n; j++)
108                 scanf("%d", &Map[i][j]);
109         }
110         cntx = cnty = n;
111         printf("%d\n", KM());
112     }
113     return 0;
114 }

posted @ 2018-04-15 16:22 _努力努力再努力x 阅读(13990) 评论(2) 编辑收藏举报

刷新页面返回顶部

努力努力再努力x