POJ-1422 Air Raid---二分图匹配&最小路径覆盖

题目链接：

https://vjudge.net/problem/POJ-1422

题目大意：

有n个点和m条有向边，现在要在点上放一些伞兵，然后伞兵沿着图走，直到不能走为止
每条边只能是一个伞兵走过，问最少放多少个伞兵

解题思路：

最小路径覆盖

最小路径覆盖=|G|-最大匹配数

重点是，建图的时候，把每个点分成两部分A1，A2，如果有边A->B,就在二分图上加A1->B2

这里的巧妙可以看下面的例子

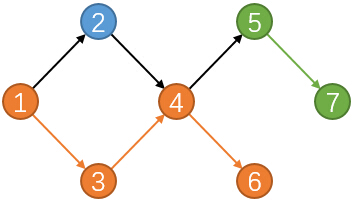
对于一条路径，起点的入度为0，终点的出度为0，中间节点的出入度都为1。

每一个点最多只能有1个后继，同时每一个点最多只能有1个前驱。

假如我们选择了一条边(u,v)，也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。

利用这个我们可以这样来构图：

将每一个点拆分成2个，分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部，所有后继节点作为B部。

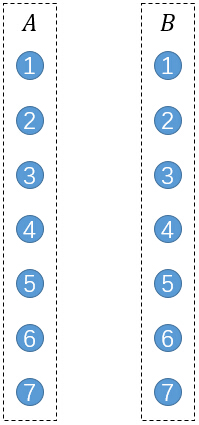
接下来进行连边，若原图中存在一条边(u,v)，则连接A部的u和B部的v。

 

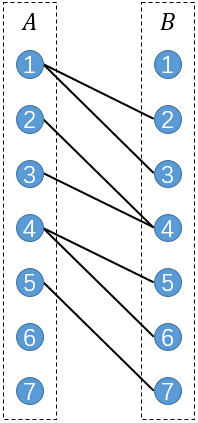
在这个上面做一个最大二分匹配：

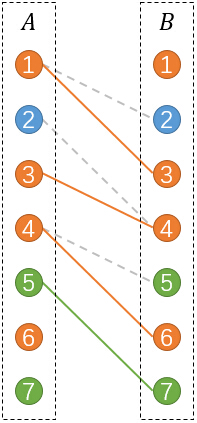
其中实线表示被选中的匹配，虚线表示未被选中的。

有没有发现，和原图刚好有着对应的关系。

这样在匹配结束的时候，我们就可以直接通过匹配的情况来确定选中的路径。

但是如何保证这样就能得到最小的路径覆盖呢？

如果一个点是路径起点的话，它在B部的节点一定是没有匹配上的。

经过最大匹配算法后，B部剩下没有被匹配的点一定是最少的，也就对应了最小需要的路径数。

所以最小路径覆盖的结果才是N-最大匹配数。

（上述例子转载自：https://blog.csdn.net/tramp_1/article/details/52742572）

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
typedef pair<int, int> Pair ;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int maxn = 300 + 10;
int T, n, m, cases;
vector<int>G[maxn];
int cx[maxn], cy[maxn];
bool vis[maxn];
bool dfs(int u)
{
    for(int i = 0; i < G[u].size(); i++)
    {
        int v = G[u][i];
        if(!vis[v])
        {
            vis[v]  =1;//加入增广路
            if(cy[v] == -1 || dfs(cy[v]))
            {
                cx[u] = v;
                cy[v] = u;
                return 1;
            }
        }
    }
    return 0;
}
int maxmatch()
{
    int ans = 0;
    memset(cx, -1, sizeof(cx));
    memset(cy, -1, sizeof(cy));
    for(int i = 1; i <= n; i++)
    {
        if(cx[i] == -1)
        {
            memset(vis, 0, sizeof(vis));
            ans += dfs(i);
        }
    }
    return ans;
}
int main()
{
    cin >> T;
    while(T--)
    {
        scanf("%d%d", &n, &m);
        int x, y;
        for(int i = 0; i <= n; i++)G[i].clear();
        for(int i = 1; i <= m; i++)
        {
            scanf("%d%d", &x, &y);
            G[x].push_back(y);
        }
        cout<<(n - maxmatch())<<endl;
    }
    return 0;
}