二分图匹配---匈牙利算法

转载：https://blog.csdn.net/c20180630/article/details/70175814

（虽然是转载，但是修改了里面的代码，加了一些解释，代码可以直接过POJ-3041）

二分图的概念

二分图又称作二部图，是图论中的一种特殊模型。
设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在X中，另一个在Y中，则称图G为二分图。

二分图的性质

定理：当且仅当无向图G的每一个回路的次数均是偶数时，G才是一个二分图。如果无回路，相当于任一回路的次数为0，故也视为二分图。

二分图的判定

如果一个图是连通的，可以用如下的方法判定是否是二分图：
在图中任选一顶点v，定义其距离标号为0，然后把它的邻接点的距离标号均设为1，接着把所有标号为1的邻接点均标号为2（如果该点未标号的话），如图所示，以此类推。
标号过程可以用一次BFS实现。标号后，所有标号为奇数的点归为X部，标号为偶数的点归为Y部。
接下来，二分图的判定就是依次检查每条边，看两个端点是否是一个在X部，一个在Y部。
如果一个图不连通，则在每个连通块中作判定。

二分图匹配

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
图中加粗的边是数量为2的匹配。

最大匹配

选择边数最大的子图称为图的最大匹配问题(maximal matching problem)
如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。
图中所示为一个最大匹配，但不是完全匹配。

增广路径

增广路径的定义：设M为二分图G已匹配边的集合，若P是图G中一条连通两个未匹配顶点的路径（P的起点在X部，终点在Y部，反之亦可），并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。
增广路径是一条“交错轨”。也就是说, 它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且起点和终点还没有被选择过，这样交错进行,显然P有奇数条边（为什么？）

寻找增广路


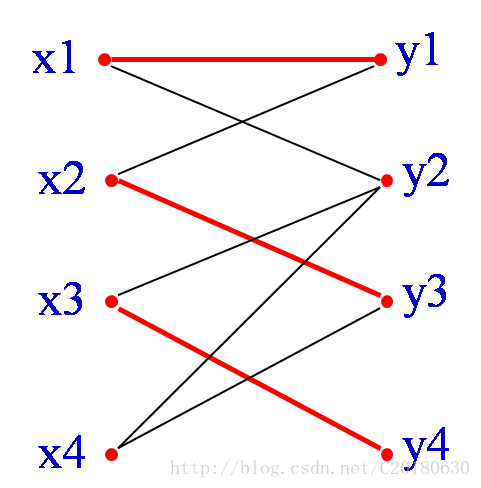
红边为三条已经匹配的边。从X部一个未匹配的顶点x4开始，找一条路径：
x4,y3,x2,y1,x1,y2x4,y3,x2,y1,x1,y2
因为y2是Y部中未匹配的顶点，故所找路径是增广路径。
其中有属于匹配M的边为{x2,y3},{x1,y1}
不属于匹配的边为{x4,y3},{x2, y1}, {x1,y2}
可以看出：不属于匹配的边要多一条！


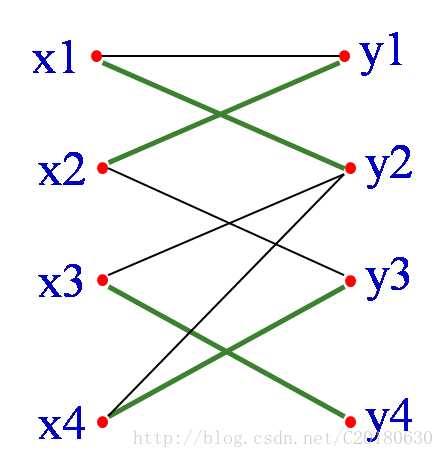
如果从M中抽走{x2,y3},{x1,y1}，并加入{x4,y3},{x2, y1}, {x1,y2}，也就是将增广路所有的边进行”反色”,则可以得到四条边的匹配M’={{x3,y4}, {x4,y3},{x2, y1}, {x1,y2}}
容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对。另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路.
可知四条边的匹配是最大匹配

增广路径性质

由增广路的定义可以推出下述三个结论：

  1. P的路径长度必定为奇数，第一条边和最后一条边都不属于M，因为两个端点分属两个集合，且未匹配。
  2. P经过取反操作可以得到一个更大的匹配M’。
  3. M为G的最大匹配当且仅当不存在相对于M的增广路径。

匈牙利算法

用增广路求最大匹配(称作匈牙利算法，匈牙利数学家Edmonds于1965年提出)
算法轮廓：

  1. 置M为空
  2. 找出一条增广路径P，通过取反操作获得更大的匹配M’代替M
  3. 重复2操作直到找不出增广路径为止

找增广路径的算法

我们采用DFS的办法找一条增广路径：
从X部一个未匹配的顶点u开始，找一个未访问的邻接点v（v一定是Y部顶点）。对于v，分两种情况：

  1. 如果v未匹配，则已经找到一条增广路
  2. 如果v已经匹配，则取出v的匹配顶点w(w一定是X部顶点)，边(w,v)目前是匹配的，根据“取反”的想法，要将(w,v)改为未匹配，(u,v)设为匹配，能实现这一点的条件是看从w为起点能否新找到一条增广路径P’。如果行，则u-v-P’就是一条以u为起点的增广路径。

匈牙利算法

cx[i]表示与X部i点匹配的Y部顶点编号
cy[i]表示与Y部i点匹配的X部顶点编号

 1 #include<iostream>
 2 #include<cstring>
 3 using namespace std;
 4 const int maxn = 500 + 10;
 5 int n, m;
 6 int Map[maxn][maxn];//map[i][j]=1表示X部的i和Y部的j存在路径
 7 int cx[maxn], cy[maxn];
 8 bool vis[maxn];
 9 //cx[i]表示X部i点匹配的Y部顶点的编号
10 //cy[i]表示Y部i点匹配的X部顶点的编号
11 
12 bool dfs(int u)//dfs进入的都是X部的点
13 {
14     for(int v = 1; v <= n; v++)//枚举Y部的点，判断X部的u和Y部的v是否存在路径
15     {
16         //如果存在路径并且还没被标记加入增广路
17         if(Map[u][v] && !vis[v])//vis数组只标记Y组
18         {
19             vis[v] = 1;//标记加入增广路
20 
21             //如果Y部的点v还未被匹配
22             //或者已经被匹配了，但是可以从v点原来匹配的cy[v]找到一条增广路
23             //说明这条路就可是一个正确的匹配
24             if(cy[v] == -1 || dfs(cy[v]))
25             {
26                 cx[u] = v;//可以匹配，进行匹配
27                 cy[v] = u;
28                 return 1;
29             }
30         }
31     }
32     return 0;//不能匹配
33 }
34 int maxmatch()//匈牙利算法主函数
35 {
36     int ans = 0;
37     memset(cx, -1, sizeof(cx));
38     memset(cy, -1, sizeof(cy));
39     for(int i = 1; i <= n; i++)
40     {
41         if(cx[i] == -1)//如果X部的i还未匹配
42         {
43             memset(vis, 0, sizeof(vis));//每次找增广路的时候清空vis
44             ans += dfs(i);
45         }
46     }
47     return ans;
48 }
49 int main()
50 {
51     cin >> n >> m;
52     int x, y;
53     for(int i = 0; i < m; i++)
54     {
55         cin >> x >> y;
56         Map[x][y] = 1;
57     }
58     cout<<maxmatch()<<endl;
59 }

 

算法分析

算法的核心是找增广路径的过程DFS
对于每个可以与u匹配的顶点v，假如它未被匹配，可以直接用v与u匹配；
如果v已与顶点w匹配，那么只需调用dfs(w)来求证w是否可以与其它顶点匹配，如果dfs(w)返回true的话，仍可以使v与u匹配；如果dfs(w)返回false,则检查u的下一个邻接点…….
在dfs时，要标记访问过的顶点（visit[j]=true），以防死循环和重复计算；每次在主过程中开始一次dfs前，所有的顶点都是未标记的。
主过程只需对每个X部的顶点调用dfs，如果返回一次true，就对最大匹配数加一；一个简单的循环就求出了最大匹配的数目。

时空分析

时间复杂度：

找一次增广路径的时间为：

邻接矩阵： O(n^2)

邻接表：O(n+m)

总时间：

邻接矩阵：O(n^3)

邻接表：O(nm)

空间复杂度：

  • 邻接矩阵：O(n^2)
  • 邻接表： O(m+n)

 

posted @ 2018-04-14 11:10  _努力努力再努力x  阅读(335)  评论(0)  编辑  收藏  举报