Codeforces Round #181 (Div. 2) C. Beautiful Numbers(组合数取模+乘法逆元)

http://codeforces.com/contest/300/problem/C

题意：一个n位的数只包含a，b两个数字并且每一位数字的和也只包含这两个数字，求这样的数有多少？

做法：枚举a出现的次数为x，则b为n-x。如果sum = ax+b(n-x)合法，则这种情况的数目为C(n,x).

C(n,x) = n! / ( (n-x)!  *  x! ) (mod p) =  n! * inv( (n-x)!  *  x!)  {inv(a)为a的乘法逆元}。

 

求乘法逆元的方法（a存在mod p的乘法逆元当且仅当a与m互质）：

   a^{-1} \equiv x \pmod{m}. => ax \equiv aa^{-1} \equiv 1 \pmod{m}.

 

法一：扩展欧几里德定理

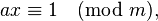ax \equiv 1 \pmod{m},  =>  ax - 1 = qm.\,  =>  ax - qm = 1,\,

 

法二：欧拉定理(结合快速幂)

根据欧拉定理，如果a与m互质，则有 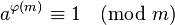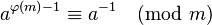a^{\varphi(m)} \equiv 1 \pmod{m}  =>  a^{\varphi(m)-1} \equiv a^{-1} \pmod{m}    (φ(m)为m的欧拉函数,即少于或等于m的数中与m互质的数的数目)

特殊的，当m为素数时，少于或等于m的数中与m互质的数的数目为m-1，即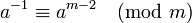\! a^{-1} \equiv a^{m-2} \pmod{m}

法二 
 1 /*
 2  *Author:       Zhaofa Fang
 3  *Created time: 2013-04-25-18.24
 4  *Language:     C++
 5  */
 6 #include <cstdio>
 7 #include <cstdlib>
 8 #include <sstream>
 9 #include <iostream>
10 #include <cmath>
11 #include <cstring>
12 #include <algorithm>
13 #include <string>
14 #include <utility>
15 #include <vector>
16 #include <queue>
17 #include <map>
18 #include <set>
19 using namespace std;
20 
21 typedef long long ll;
22 #define DEBUG(x) cout<< #x << ':' << x << endl
23 #define FOR(i,s,t) for(int i = (s);i <= (t);i++)
24 #define FORD(i,s,t) for(int i = (s);i >= (t);i--)
25 #define REP(i,n) for(int i=0;i<n;i++)
26 #define REPD(i,n) for(int i=n-1;i>=0;i--)
27 #define PII pair<int,int>
28 #define PB push_back
29 #define MP make_pair
30 #define ft first
31 #define sd second
32 #define lowbit(x) (x&(-x))
33 #define INF (1<<30)
34 
35 const ll mod = 1000000007;
36 
37 ll fac[1000111];
38 
39 
40 void init(int n){
41     fac[0] = 1;
42     FOR(i,1,n){
43         fac[i] = fac[i-1]*i%mod;
44     }
45 }
46 ll pow_mod(ll a,ll m,ll n){
47     ll tmp = 1;
48     a%=n;
49     while(m){
50         if(m&1)tmp = tmp*a%n;
51         a = a*a%n;
52         m>>=1;
53     }
54     return tmp;
55 }
56 
57 bool check(int a,int b,int sum){
58     while(sum>0){
59         int tmp = sum%10;
60         if(tmp!=a&&tmp!=b)return false;
61         sum/=10;
62     }
63     return true;
64 }
65 int main(){
66     //freopen("in","r",stdin);
67     //freopen("out","w",stdout);
68     int a,b,n;
69     scanf("%d%d%d",&a,&b,&n);
70     ll ans = 0;
71     init(n);
72     REP(i,n+1){
73         int x = i;
74         int y = n - i;
75         int sum = a*x + b*y;
76         if(check(a,b,sum)){
77             ll tmp = fac[n]*pow_mod(fac[y]*fac[x],mod-2,mod)%mod;
78             ans = (ans + tmp)%mod;
79         }
80     }
81     cout<<ans<<endl;
82     return 0;
83 }

 

附：维基的资料

posted @ 2013-04-27 20:45  發_  阅读(636)  评论(0)  编辑  收藏  举报