洛谷题单 算法1-4 递推与递归
1 地毯填补问题
题目描述
相传在一个古老的阿拉伯国家里,有一座宫殿。宫殿里有个四四方方的格子迷宫,国王选择驸马的方法非常特殊,也非常简单:公主就站在其中一个方格子上,只要谁能用地毯将除公主站立的地方外的所有地方盖上,美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住,毯子的形状有所规定,只能有四种选择(如图):
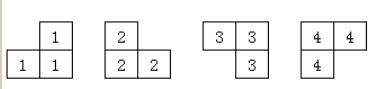
并且每一方格只能用一层地毯,迷宫的大小为 2^k* 2^k的方形。当然,也不能让公主无限制的在那儿等,对吧?由于你使用的是计算机,所以实现时间为1s。
输入格式
输入文件共 2行。
第一行:k,即给定被填补迷宫的大小为 2^k* 2^k(0<k≤10);
第二行:x,y,即给出公主所在方格的坐标(x 为行坐标,y 为列坐标),x 和 y 之间有一个空格隔开。
输出格式
将迷宫填补完整的方案:每一行为x y c(x,y 为毯子拐角的行坐标和列坐标, c 为使用毯子的形状,具体见上面的图 1,毯子形状分别用 1,2,3,4 表示,x,y,c 之间用一个空格隔开)。
输入输出样例
输入 #1复制
3
3 3
输出 #1复制
5 5 1
2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1
思路:分治思想。顾名思义,分而治之。这道题本蒟蒻做了好久好久~~~ 先看思路。
先假设k=1,那么公主站立的位置只能有4种情况。而对于这四种情况,我们可以对应四种毯子来处理。
看k=2的情况,我们先判断特殊点(即公主站立的位置),我们发现,无论公主站在什么位置,我们都可以将整个的大方格分成四个2*2的小方格。找到公主站立的位置,我们可以根据k=1时的情况来处理,那么剩下的三个方格怎么办呢?我们考虑,是不是可以给每个格子增加一个特殊点,来按照上面的方法处理呢?通过观察我们发现,这种做法是可以的。这样一来,整个问题就被分成了若干个小问题,交给计算机去递归就好了。
那么k>2时的情况是怎么样的呢?通过画图,我们可以发发现,无论k是几,我们总能按照上面的思想将问题分成若干个小问题去处理。具体实现可以看代码。

import java.util.Scanner;
public class Main {
static int k,x0,y0;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
k = sc.nextInt();
x0= sc.nextInt();
y0=sc.nextInt();
dfs(x0,y0,1,1,1<<k);
}
public static void dfs(int x,int y,int zx,int zy,int len){
//x y 为我们要处理的点的坐标 zx zy为我们处理的格子的左上角的坐标 len为我们当前处理格子的边长
if(len==1){
return ;
}
len/=2;
if(x-zx<len&&y-zy<len){ //我们要处理的点位于当前格子的左上角
System.out.println((zx+len)+" "+(zy+len)+" 1");//将大格子中间位置进行处理 进行分治
dfs(x,y,zx,zy,len);//继续递归处理左上角
dfs(zx+len-1,zy+len,zx,zy+len,len);//继续递归处理右上角
dfs(zx+len,zy+len-1,zx+len,zy,len);//继续递归处理左下角
dfs(zx+len,zy+len,zx+len,zy+len,len);//继续递归处理右下角
}else if(x-zx<len&&y-zy>=len){//我们要处理的点位于当前格子的右上角
System.out.println((zx+len)+" "+(zy+len-1)+" 2");
dfs(zx+len-1,zy+len-1,zx,zy,len);
dfs(x,y,zx,zy+len,len);
dfs(zx+len,zy+len-1,zx+len,zy,len);
dfs(zx+len,zy+len,zx+len,zy+len,len);
}else if(x-zx>=len&&y-zy<len){//我们要处理的点位于当前格子的左下角
System.out.println((zx+len-1)+" "+(zy+len)+" 3");
dfs(zx+len-1,zy+len-1,zx,zy,len);
dfs(zx+len-1,zy+len,zx,zy+len,len);
dfs(x,y,zx+len,zy,len);
dfs(zx+len,zy+len,zx+len,zy+len,len);
}else{//我们要处理的点位于当前格子的右下角
System.out.println(zx+len-1+" "+(zy+len-1)+" 4");
dfs(zx+len-1,zy+len-1,zx,zy,len);
dfs(zx+len-1,zy+len,zx,zy+len,len);
dfs(zx+len,zy+len-1,zx+len,zy,len);
dfs(x,y,zx+len,zy+len,len);
}
}
}
2 外星密码
题目描述
有了防护伞,并不能完全避免 2012 的灾难。地球防卫小队决定去求助外星种族的帮 助。经过很长时间的努力,小队终于收到了外星生命的回信。但是外星人发过来的却是一 串密码。只有解开密码,才能知道外星人给的准确回复。解开密码的第一道工序就是解压 缩密码,外星人对于连续的若干个相同的子串“X”会压缩为“[DX]”的形式(D 是一个整 数且 1≤D≤99),比如说字符串“CBCBCBCB”就压缩为“[4CB]”或者“[2[2CB]]”,类 似于后面这种压缩之后再压缩的称为二重压缩。如果是“[2[2[2CB]]]”则是三重的。现 在我们给你外星人发送的密码,请你对其进行解压缩。
输入格式
第一行:一个字符串
输出格式
第一行:一个字符串
输入输出样例
输入
AC[3FUN]
输出
ACFUNFUNFUN
说明/提示
【数据范围】
对于 50%的数据:解压后的字符串长度在 1000 以内,最多只有三重压缩。
对于 100%的数据:解压后的字符串长度在 20000 以内,最多只有十重压缩。 对于 100%的数据:保证只包含数字、大写字母、’[‘和’]‘
思路:看到这道题,不难想到应该递归着去做。我的思路是将字符串储存在数组中,然后根据每次遇到 ’[ ‘便进行解压,解压的次数我们很容易得出。进而只需要我们去遍历这个数组,当我们遇到’ ] ‘的时候返回遍历得到的字符串,然后乘以相应的循环次数即可。重点来了,我们遇到第一个’ ] '便返回了,那么如果第一个右括号右边还有需要解压的数据怎么办呢?想一下,括号成对出现,去掉了一个右括号必然去掉一个左括号。也就意味着这组待解压的数据我们已经解压完成了,我们继续解压后面的数据就好了。也就是说,在左括号的地方再加一次递归,用以获取后面的数据就好了。
import java.util.Scanner;
public class Main {
static String str = "",ans="";
static char[] ch;
static int maxIndex=-1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
str = sc.next();
ch = str.toCharArray();
ans=fun(0);
System.out.println(ans);
}
public static String fun(int index){
maxIndex = Math.max(index,maxIndex);
int k = 0;
String s ="";
if(index==ch.length){
return "";
}
if(ch[index]>='0'&&ch[index]<='9'){
k = ch[index]-'0';
if((index+1)<ch.length&&ch[index+1]>='0'&&ch[index+1]<='9'){
k = k*10+(ch[index+1]-'0');
index++;
}
String t =fun(index+1);
for(int i=0;i<k;i++){
s+=t;
}
}else if(ch[index]>='A'&&ch[index]<='Z'){
s = ch[index]+fun(index+1);
}else if(ch[index]=='['){
s = fun(index+1);
s+=fun(maxIndex+1);
}else if(ch[index]==']'){
return "";
}
return s;
}
}
3 栈
题目背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述

宁宁考虑的是这样一个问题:一个操作数序列,1,2,…,n(图示为 1 到 3 的情况),栈 A 的深度大于 n。
现在可以进行两种操作,
将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的 push 操作)
将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的 pop 操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由 1 2 3 生成序列 2 3 1 的过程。

(原始状态如上图所示)
你的程序将对给定的 n,计算并输出由操作数序列 1,2,…,n 经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数 n(1≤n≤18)。
输出格式
输出文件只有一行,即可能输出序列的总数目。
输入输出样例
输入
3
输出
5
思路:看大佬们写的题解,说可以用卡特兰数做,然而 菜鸡的我并不知道什么是卡特兰数 ,这不重要。。。此题用记忆化搜索做,十分简单。也不需要用dp去推状态转移方程。我们用count数组储存队列中剩余x个数,栈中剩余y个数时的情况数,那么当x=1时,我们只能有一种情况(出栈)。当栈不为空时,我们可以选择出栈或者入栈。因为记忆化搜索,所以数组数大于0的时候return即可。
import java.util.Scanner;
public class Main {
static long n,ans;
static long[][] count;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextLong();
count = new long[(int) (n+1)][(int) (n+1)];
System.out.println(dfs(n,0));
}
public static long dfs(long x,int y){ //队列中剩余x个数 栈中剩余y个数时的情况数
if(count[(int) x][y]!=0){
return count[(int) x][y];
}
if(x==0) return 1; //栈中没有数 则只能有一种情况
if(y>0) count[(int) x][y]+=dfs(x,y-1);
count[(int) x][y]+=dfs(x-1,y+1);
return count[(int) x][y];
}
}
4 黑白棋子的移动
题目描述
有 2n 个棋子排成一行,开始为位置白子全部在左边,黑子全部在右边,如下图为 n=5 的情况:
○○○○○●●●●●
移动棋子的规则是:每次必须同时移动相邻的两个棋子,颜色不限,可以左移也可以右移到空位上去,但不能调换两个棋子的左右位置。每次移动必须跳过若干个棋子(不能平移),要求最后能移成黑白相间的一行棋子。如 n=5 时,成为:
○●○●○●○●○●
任务:编程打印出移动过程。
输入格式
一个整数 n。
输出格式
若干行,表示初始状态和每次移动的状态,用"o"表示白子,"*“表示黑子,”-"表示空行。
输入输出样例
输入
7
输出
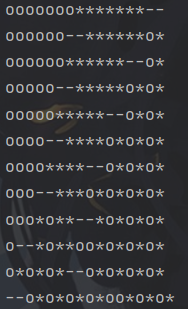
说明/提示
4≤n≤100
思路:分治。通过观察样例,我们发现,当待排序棋子数量>4时,棋子仅需两步就可以完成排序,而排序完成以后,我们只需要继续处理n-1的情况。也就是说,整个问题可以划分为n更小的问题去解决。当待排序棋子数量>4时,棋子仅需两步就可以完成排序,而我们发现当剩余待排序棋子数量为2*4的时候,规律发生了变化。但是没关系,对于n=4的情特判一下就好了。
import java.util.Scanner;
public class Main {
static int n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
fun(n);
}
public static void fun(int k){
if(k==4){
String s1 = "oooo****";
String s2 = "ooo--***o*";
String s3 = "ooo*o**--*";
String s4 = "o--*o**oo*";
String s5 = "o*o*o*--o*";
String s6 = "--o*o*o*o*";
s1+="--";
for(int i=0;i<n-4;i++){
s1+="o*";
s2+="o*";
s3+="o*";
s4+="o*";
s5+="o*";
s6+="o*";
}
System.out.println(s1+"\n"+s2+"\n"+s3+"\n"+s4+"\n"+s5+"\n"+s6);
return ;
}else{
String s1 ="";
String s2 ="";
for(int i=0;i<k;i++){
s1+="o";
}
for(int i=0;i<k;i++){
s1+="*";
}
for(int i=0;i<k-1;i++){
s2+="o";
}
s2+="--";
for(int i=0;i<k-1;i++){
s2+="*";
}
s1+="--";
for(int i=0;i<n-k;i++){
s1+="o*";
s2+="o*";
}
s2+="o*";
System.out.println(s1+"\n"+s2);
fun(k-1);
}
}
}
5 数的计算
题目描述
我们要求找出具有下列性质数的个数(包含输入的自然数n):
先输入一个自然数n(n≤1000),然后对此自然数按照如下方法进行处理:
不作任何处理;
在它的左边加上一个自然数,但该自然数不能超过原数的一半;
加上数后,继续按此规则进行处理,直到不能再加自然数为止.
输入格式
1个自然数n(n≤1000)
输出格式
1个整数,表示具有该性质数的个数。
输入输出样例
输入
6
输出
6
说明/提示
满足条件的数为
6,16,26,126,36,136
思路:dfs爆搜,超时了。。需要用dp或者说递推的思想来做。首先,用爆搜出来的数据打印一下n取不同值时的结果来找一下规律。
n=0, n=1时,答案是1
n=2, ans=2; n=3,ans=2
n=4,ans=4; n=5,ans=4
n=6,ans=6; n=7,ans=6
n=8,ans=10 n=9,ans=10
n=10,ans=14…
把数据打印出来以后,很明显答案存在规律。
当n%2=1时,f[n]=f[n-1]。
当n%2=0时,f[n] =f[n-1]+f[n/2]。
至此,此题结束。本菜鸡除了爆搜啥也不会。
其实此题还有一种做法,就是打表,利用我们写的dfs,把答案储存起来就好了。。
ac代码:
import java.util.Scanner;
public class Main {
static int n,ans=1;
static int[] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
f= new int[n+1];
f[0]=1;
f[1]=1;
for(int i=2;i<=n;i++){
if(i%2==0){
f[i] = f[i-1]+f[i/2];
}else{
f[i] = f[i-1];
}
}
System.out.println(f[n]);
}
}
超时代码:
import java.util.Scanner;
public class Main {
static int[] count;
static int n,ans=1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
count = new int[n+1];
dfs(n);
System.out.println(ans);
}
public static void dfs(int x){
for(int i=1;i<=x/2;i++){
ans++;
dfs(i);
}
}
}
6 幂次方
题目描述
任何一个正整数都可以用 2 的幂次方表示。例如 137=2^7 + 2 ^3+ 2^0。
同时约定方次用括号来表示,即 a^b可表示为 a(b)。
由此可知,137可表示为 2(7)+2(3)+2(0)
进一步:
7= 2^2 +2+2^0
( 2^1 用 2表示),并且 3=2+2^0。
所以最后 137可表示为 2(2(2)+2+2(0))+2(2+2(0))+2(0)。
又如 1315 最后可表示为 2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)。
输入格式
一行一个正整数 n。
输出格式
符合约定的 n的 0,2 表示(在表示中不能有空格)。
输入输出样例
输入
1315
输出
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
思路:模拟递归。将n分解为二进制,比如1010(十进制的10),此时遍历每个不为0的数位,假设此数位代表的数为2的k次方。根据题意可以看出,k>2的时候是可以继续递归分解的,而k<=2的时候不能继续分解了,当k=0||k=2的时候输出2(0)||2(2),而k=1的时候直接输出2就好。
对于括号和加号要特别注意,何时输出括号,何时输出加号。
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
static int n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
char[] ch = Integer.toBinaryString(n).toCharArray();
ok(ch);
}
public static void ok(char[] ch){
boolean flag = false;
for(int i=0,t=ch.length-1;i<ch.length;i++,t--){
if(ch[i]!='0'){
if(flag){
System.out.print("+");
}
flag = true;
if(t==0){
System.out.print("2(0)");
}else if(t==1){
System.out.print("2");
}else if(t==2){
System.out.print("2(2)");
}else{
System.out.print("2(");
char[] c1 = Integer.toBinaryString(t).toCharArray();
ok(c1);
System.out.print(")");
}
}
}
}
}
7 小A点菜
题目背景
uim神犇拿到了uoi的ra(镭牌)后,立刻拉着基友小A到了一家……餐馆,很低端的那种。
uim指着墙上的价目表(太低级了没有菜单),说:“随便点”。
题目描述
不过uim由于买了一些辅(e)辅(ro)书,口袋里只剩M元(M≤10000)。
餐馆虽低端,但是菜品种类不少,有N种(N≤100),第i种卖ai元(ai ≤1000)。由于是很低端的餐馆,所以每种菜只有一份。
小A奉行“不把钱吃光不罢休”,所以他点单一定刚好吧uim身上所有钱花完。他想知道有多少种点菜方法。
由于小A肚子太饿,所以最多只能等待1秒。
输入格式
第一行是两个数字,表示N和M。
第二行起N个正数ai(可以有相同的数字,每个数字均在1000以内)。
输出格式
一个正整数,表示点菜方案数,保证答案的范围在int之内。
输入输出样例
输入
4 4
1 1 2 2
输出
3
思路:01背包求方案数。题目求的是恰好花完m元时的情况数,我们定义一个二维数组f,储存方案数。
其中 f[i][j] 表示判断i件菜品恰好花完j元时的方案数
1 :初始化
f[i][0] = 1 表示有i件菜品恰好花完0元时只有一种方案
f[0][j] = 0 表示有0件物品恰好花完j元时是不可能的 只能有0种方案 j!=0
2: 状态转移方程
if(j<a[i]) f[i][j] = f[i-1][j]
if(j>=a[i]) f[i][j] = f[i-1][j]+f[i-1][j-a[i]]
至此,思路此题就可以结束了。但是我们都知道,背包问题是可以在空间上进行优化的,我们可以把二维数组优化为一维数组。代码如下:
空间优化后的代码:
import java.util.Scanner;
public class Main {
static int n,m;
static int[] a,ans;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
a = new int[n+1];
ans = new int[m+1];
for(int i=1;i<=n;i++){
a[i] = sc.nextInt();
}
ans[0] = 1;
for(int i=1;i<=n;i++){
for(int j=m;j>=a[i];j--){
ans[j] = ans[j]+ans[j-a[i]];
}
}
System.out.print(ans[m]);
}
}
没有优化的代码:
import java.util.Scanner;
public class Main {
static int n,m;
static int[] a;
static int[][] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
a = new int[n+1];
f = new int[n+1][m+1];
for(int i=1;i<=n;i++){
a[i] = sc.nextInt();
}
for(int i=0;i<=n;i++){
f[i][0] = 1;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(j<a[i]) f[i][j] = f[i-1][j];
if(j>=a[i]) f[i][j] = f[i-1][j]+f[i-1][j-a[i]];
}
}
System.out.print(f[n][m]);
}
}
8 南蛮图腾
题目描述
自从到了南蛮之地,孔明不仅把孟获收拾的服服帖帖,而且还发现了不少少数民族的智慧,他发现少数民族的图腾往往有着一种分形的效果,在得到了酋长的传授后,孔明掌握了不少绘图技术,但唯独不会画他们的图腾,于是他找上了你的爷爷的爷爷的爷爷的爷爷……帮忙,作为一个好孙子的孙子的孙子的孙子……你能做到吗?
输入格式
每个数据一个数字,表示图腾的大小(此大小非彼大小) n<=10
输出格式
这个大小的图腾
输入输出样例
输入
2
输出

输入
3
输出

思路:找一下规律,我们会发现,n = 2的情况是由n =1复制而来的。n=3的情况是由n=2复制而来的。。。蒟蒻不懂什么分治,暴力模拟就完了。。。另外,我觉得用字符串数组储存比用字符数组储存要简单的多,获得n以后,直接复制,注意空格!!!
膜拜打表的大哥!
import java.util.Scanner;
public class Main {
static int n;
static String[] ans ;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
ans = new String[(1<<n)+1];
ans[1]="/\\";
ans[2]="/__\\";
for(int i=2;i<=n;i++){
fun(i);
}
for(int i=1;i<=(1<<n);i++){
for(int j=0;j<((1<<n)-i);j++){
System.out.print(" ");
}
System.out.println(ans[i]);
}
}
public static void fun(int k){ //第k个图腾 需要复制高度1<<(k-1)
int h0 = 1<<(k-1);
int h1 = 1<<k;
for(int i=h0+1;i<=h1;i++){
ans[i] = ans[i-h0] ;
int temp = (1<<k)-2-2*(i-(1<<(k-1))-1);
for(int j=0;j<temp;j++){
ans[i]+=" ";
}
ans[i] +=ans[i-h0] ;
}
}
}
9 Function
题目描述
对于一个递归函数w(a,b,c)
如果a≤0 or b≤0 or c≤0就返回值1.
如果a>20 or b>20 or c>20就返回w(20,20,20)
如果a<b并且b<c 就返回w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c)
其它的情况就返回w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1)
这是个简单的递归函数,但实现起来可能会有些问题。当a,b,c均为15时,调用的次数将非常的多。你要想个办法才行.
absi2011 : 比如 w(30,−1,0)既满足条件1又满足条件2
这种时候我们就按最上面的条件来算
所以答案为1
输入格式
会有若干行。
并以−1,−1,−1结束。
保证输入的数在[-9223372036854775808,9223372036854775807]之间,并且是整数。
输出格式
输出若干行,每一行格式:
w(a, b, c) = ans
注意空格。
输入输出样例
输入
1 1 1
2 2 2
-1 -1 -1
输出
w(1, 1, 1) = 2
w(2, 2, 2) = 4
思路:题目已经提示了,爆搜应该会超时,我们采用记忆化搜索,储存一下结果就好了。
import java.util.Scanner;
public class Main {
static long a,b,c;
static boolean[][][] flag = new boolean[25][25][25];
static long[][][] book = new long[25][25][25];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(true){
a = sc.nextLong();
b = sc.nextLong();
c = sc.nextLong();
if(a==-1&&b==-1&&c==-1){
break;
}
System.out.println("w("+a+", "+b+", "+c+") = "+fum(a,b,c));
}
}
public static long fum(long q,long w,long e){
if(q<=0||w<=0||e<=0){
return 1;
}else if(q>20||w>20||e>20){
return fum(20,20,20);
}
if(flag[(int) q][(int) w][(int) e]){
return book[(int) q][(int) w][(int) e];
}
if(q<w&&w<e){
flag[(int) q][(int) w][(int) e]=true;
book[(int) q][(int) w][(int) e] = fum(q,w,e-1)+fum(q,w-1,e-1)-fum(q,w-1,e);
return book[(int) q][(int) w][(int) e];
}else{
flag[(int) q][(int) w][(int) e]=true;
book[(int) q][(int) w][(int) e]= fum(q-1,w,e)+fum(q-1,w-1,e)+fum(q-1,w,e-1)-fum(q-1,w-1,e-1);
return book[(int) q][(int) w][(int) e];
}
}
}
10 蜜蜂路线
题目描述
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房 m开始爬到蜂房 n,m<n,有多少种爬行路线?(备注:题面有误,右上角应为 n−1)
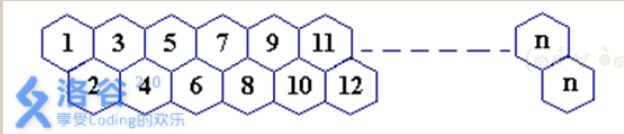
输入格式
输入 m,n 的值
输出格式
爬行有多少种路线
输入输出样例
输入
1 14
输出
377
说明/提示
对于100%的数据,M,N≤1000
思路:dp,水题,注意一下高精度,没啥好说的。。。
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
static int m,n,x0,y0,x1,y1,tx,ty;
static BigInteger[][] dp = new BigInteger[510][510];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
m = sc.nextInt();
n = sc.nextInt();
if(m%2==0){
x0 = 1;
y0 = m/2;
dp[0][y0]=BigInteger.ZERO;
dp[1][y0-1]=BigInteger.ZERO;
}else{
x0 = 0;
y0 = m/2+1;
dp[0][y0-1]=BigInteger.ZERO;
dp[1][y0-1]=BigInteger.ZERO;
}
dp[x0][y0]=BigInteger.ONE;
if(n%2==0){
x1 = 1;
y1 = n/2;
}else{
x1 = 0;
y1 = n/2+1;
}
for(int i=m+1;i<=n;i++){
if(i%2==0){
tx = 1;
ty= i/2;
dp[tx][ty]=dp[1][ty-1].add(dp[0][ty]);
}else{
tx = 0;
ty= i/2+1;
dp[tx][ty]=dp[0][ty-1].add(dp[1][ty-1]);
}
}
System.out.println(dp[x1][y1]);
}
}
11 过河卒
题目描述
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A 点 (0,0)、B 点 (n,m),同样马的位置坐标是需要给出的。

现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 B 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
输入输出样例
输入 #1复制
6 6 3 3
输出 #1复制
6
说明/提示
对于 100% 的数据,1≤n,m≤20,0≤ 马的坐标≤20。
思路 :记忆化搜索或者dp都能过。
dp:
import java.util.Scanner;
public class Main {
static int n,m,x1,y1;
static long[][] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
x1= sc.nextInt();
y1= sc.nextInt();
dp = new long[n+1][m+1];
dp[0][0] = 1;
for(int i = 1;i<=n;i++){
if(ok(i,0)){
dp[i][0]=dp[i-1][0];
}
}
for(int j=1;j<=m;j++){
if(ok(0,j)){
dp[0][j]=dp[0][j-1];
}
}
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(dp[i][j]!=0){
continue;
}else if(ok(i,j)){
int tx = i-1;
int ty = j;
if(tx>=0&&tx<=n&&ty>=0&&ty<=m&&ok(tx,ty)){
dp[i][j]+=dp[tx][ty];
}
tx = i;
ty = j-1;
if(tx>=0&&tx<=n&&ty>=0&&ty<=m&&ok(tx,ty)){
dp[i][j]+=dp[tx][ty];
}
}
}
}
System.out.println(dp[n][m]);
}
public static boolean ok(int x,int y){
if((x==x1&&y==y1)||(x==x1-1&&y==y1-2)||(x==x1-2&&y==y1-1)||(x==x1-2&&y==y1+1)||(x==x1-1&&y==y1+2)||(x==x1+1&&y==y1-2)||(x==x1+2&&y==y1-1)||(x==x1+2&&y==y1+1)||(x==x1+1&&y==y1+2)){
return false;
}
return true;
}
}
记忆化搜索:
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
static int n,m,x1,y1;
static long[][] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
x1= sc.nextInt();
y1= sc.nextInt();
dp = new long[n+1][m+1];
dp[n][m] = 1;
dfs(0,0);
System.out.println(dp[0][0]);
}
public static boolean ok(int x,int y){
if((x==x1&&y==y1)||(x==x1-1&&y==y1-2)||(x==x1-2&&y==y1-1)||(x==x1-2&&y==y1+1)||(x==x1-1&&y==y1+2)||(x==x1+1&&y==y1-2)||(x==x1+2&&y==y1-1)||(x==x1+2&&y==y1+1)||(x==x1+1&&y==y1+2)){
return false;
}
return true;
}
public static long dfs(int x,int y){
if(dp[x][y]!=0){
return dp[x][y];
}
int tx;
int ty;
tx = x+1;
ty = y;
if(tx>=0&&tx<=n&&ty>=0&&ty<=m&&ok(tx,ty)){
dp[x][y]+=dfs(tx,ty);
}
tx = x;
ty = y+1;
if(tx>=0&&tx<=n&&ty>=0&&ty<=m&&ok(tx,ty)){
dp[x][y]+=dfs(tx,ty);
}
return dp[x][y];
}
}
未完待续。。。。。。

