Machine Learning in Action -- FP-growth
要解决的问题,频繁项集
最暴力的方法,就是遍历所有的项集组合,当然计算量过大
最典型的算法apriori, 算法核心思想,当一个集合不是频繁项集,那么它的超集也一定不是频繁项集
这个结论是很明显的,基于这样的思路,可以大大减少频繁项集的候选项
因为你只要发现一个集合非频繁项集,那么他所有的超集都可以忽略
但apriori算法的问题是,计算每个候选项的出现频率的时候都需要遍历整个数据集,这个明显是低效的
很自然的想法,就是否有办法可以尽量少的遍历数据集?比如遍历一遍就可以得到所有的项集的出现频率
那么这个就是FP-growth算法解决的问题
这个算法的典型应用,
比如在搜索引擎里面输入关键词时,后面会给出提示常用的词组合
这就需要效率很高的频繁项集挖掘算法
FP-tree
首先要构建FP-tree
只需要遍历数据集两遍,就可以完成FP-tree的构建,这个tree记录了所有频繁项集的出现频率
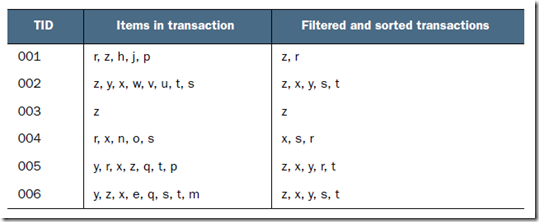
看例子,需要对如下数据集创建FP-tree
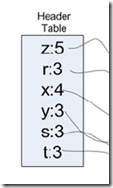
第一步,遍历数据集,计算所有元素项集的频率,即size=1的项,过滤掉非频繁项集,得到如下图的Header Table
并且对每条记录也进行过滤,过滤到非频繁的元素项,并使这条记录按照元素项的出现次数进行重新排序
第一步其实是优化或预处理,减少需要计算的频繁项集的候选集
这里之所以需要排序,因为频繁项集关注的是组合而不是排列,而后面在生成树的时候需要避免生成重复的分支
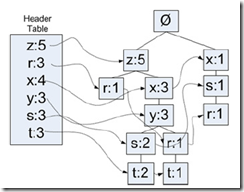
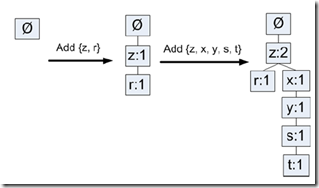
第二步,遍历数据集,构建FP-tree
构建的过程很简单,看下图就明白了
代码实现
先定义FP-tree
class treeNode: def __init__(self, nameValue, numOccur, parentNode): self.name = nameValue #node name self.count = numOccur #出现频率 self.nodeLink = None #链接到相同节点 self.parent = parentNode self.children = {} def inc(self, numOccur): self.count += numOccur def disp(self, ind=1): #用于打印树,debug用 print ' '*ind, self.name, ' ', self.count for child in self.children.values(): child.disp(ind+1)
载入数据,
def loadSimpDat(): simpDat = [['r', 'z', 'h', 'j', 'p'], ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'], ['z'], ['r', 'x', 'n', 'o', 's'], ['y', 'r', 'x', 'z', 'q', 't', 'p'], ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']] return simpDat def createInitSet(dataSet): retDict = {} for trans in dataSet: retDict[frozenset(trans)] = 1 #frozenset,即不可变set return retDict
得到的输入数据是这样的,看着比较怪,但后面递归的时候表示子串出现次数,不一定为1
>>> simpDat = fpGrowth.loadSimpDat() >>> initSet = fpGrowth.createInitSet(simpDat) >>> initSet {frozenset(['e', 'm', 'q', 's', 't', 'y', 'x', 'z']): 1, frozenset(['x','s', 'r', 'o', 'n']): 1, frozenset(['s', 'u', 't', 'w', 'v', 'y', 'x', 'z']): 1, frozenset(['q', 'p', 'r', 't', 'y', 'x', 'z']): 1,frozenset(['h', 'r', 'z', 'p', 'j']): 1, frozenset(['z']): 1}
创建FP-tree的逻辑,
def createTree(dataSet, minSup=1): #minSup,最小的support(支持度),出现次数 for trans in dataSet #初始化heaerTable,计算所有item出现的次数 for item in trans: headerTable[item] = headerTable.get(item, 0) + dataSet[trans] for k in headerTable.keys(): if headerTable[k] < minSup: #删除非频繁项集 del(headerTable[k]) freqItemSet = set(headerTable.keys()) #得到频繁项集 if len(freqItemSet) == 0: return None, None #如果没有频繁项集,直接返回 for k in headerTable: headerTable[k] = [headerTable[k], None] #扩展headerTable,存储item的次数和第一个该item的引用,初始化时,引用为none retTree = treeNode('Null Set', 1, None) for tranSet, count in dataSet.items(): #每个tran localD = {} for item in tranSet: #每个item if item in freqItemSet: #过滤非频繁项集item localD[item] = headerTable[item][0] #localD存储该tran中的频繁item和该item在headerTable中的全局频率 if len(localD) > 0: orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] #按全局频率排序 updateTree(orderedItems, retTree, headerTable, count) #用预处理过的orderedItems来更新树 return retTree, headerTable
#递归算法,每次递归只处理第一个item #并且items是排过序的,所以第一个item一定是root的children,第二个为第一个的children def updateTree(items, inTree, headerTable, count): if items[0] in inTree.children: #看root的children中是否有items[0] inTree.children[items[0]].inc(count) #有,增加count else: inTree.children[items[0]] = treeNode(items[0], count, inTree) #没有,为item[0]创建新的treenode if headerTable[items[0]][1] == None: #如果headerTable中该item的引用为空,直接指向item[0] headerTable[items[0]][1] = inTree.children[items[0]] else: # 否则说明该item已经出现过,调用updateHeader updateHeader(headerTable[items[0]][1], inTree.children[items[0]]) if len(items) > 1: #item[0]为root,继续update updateTree(items[1::], inTree.children[items[0]], headerTable, count)
#顺着headerTable的item引用,一直找到nodeLink为None, 即最后一次出现的item #然后接上 def updateHeader(nodeToTest, targetNode): while (nodeToTest.nodeLink != None): nodeToTest = nodeToTest.nodeLink nodeToTest.nodeLink = targetNode
Mining frequent items from an FP-tree
发现频繁项集的过程和apriori一样,也是逐步递增的发现,即先找到size=1的,再去找size=2的。。。。。。
其实我们有了上面构建的FP-tree,就已经找到size=1的频繁集,即header table中所有的元素项
那现在的问题就是如何基于FP-tree找到size=2的频繁项集
conditional pattern bases
首先抽取条件模式基,
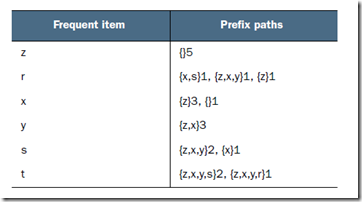
根据图,所谓条件模式基,是以每个频繁项集为结尾的,在FP-tree中所有可能的前缀路径
对应于前面的tansactioinSet
而由于前面在header table中存了每个频繁集所有出现的位置,通过链表可以很容易找到所有的条件模式基
比如,对于r,可以找到第一个r,z,第二个r,y,x,z。。。。。。
对于r,y,x,z,去掉r,然后按照全局频率排序得到z,x,y,后面的1表示r,z,x,y这个子串出现的次数
代码如下,
def ascendTree(leafNode, prefixPath): #递归找出某个树节点的前缀路径 if leafNode.parent != None: prefixPath.append(leafNode.name) ascendTree(leafNode.parent, prefixPath) def findPrefixPath(basePat, treeNode): condPats = {} while treeNode != None: prefixPath = [] ascendTree(treeNode, prefixPath) if len(prefixPath) > 1: condPats[frozenset(prefixPath[1:])] = treeNode.count treeNode = treeNode.nodeLink #到下一个频繁项集出现的位置 return condPats
>>> fpGrowth.findPrefixPath('x', myHeaderTab['x'][1]) {frozenset(['z']): 3} >>> fpGrowth.findPrefixPath('z', myHeaderTab['z'][1]) {} >>> fpGrowth.findPrefixPath('r', myHeaderTab['r'][1]) {frozenset(['x', 's']): 1, frozenset(['z']): 1, frozenset(['y', 'x', 'z']): 1}
有了每个频繁项集的条件模式基,后面需求做的
对于每个频繁项集,基于他的条件模式基建立FP-tree,这样就可以找出size=2的频繁项集
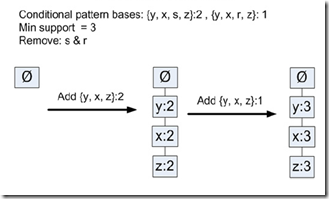
直接看例子,需要创建t的FP-tree
过程和前面建FP-tree是一样的,
先过滤非频繁项集,所以过滤掉r,s,因为在条件模式基中,s出现s×2次,而r出现r×1次
再创建FP-tree,得到频繁项集为,y,x,z
于是我们就找到size=2的频繁项集,
t,y;t,x;t,z
下面要找到size=3的频繁项集只需要重复上面的过程,找到size=2频繁项集的条件模式基,在各自构建FP-tree
代码,
#inTree,FP-tree #preFix,前缀,上面例子中的t #freqItemList,保存所有的频繁项集 def mineTree(inTree, headerTable, minSup, preFix, freqItemList): #返回headerTable中的所有的item名(v[0]),并以全局频率排序 bigL = [v[0] for v in sorted(headerTable.items(),key=lambda p: p[1])] for basePat in bigL: #上面例子,y,x,z newFreqSet = preFix.copy() #先将前缀拷过来,上面例子't' newFreqSet.add(basePat) #拼成新的频繁集,如t,y freqItemList.append(newFreqSet) #将频繁集加入freqItemList condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) #生成条件模式基,比如生成t,y的 myCondTree, myHead = createTree(condPattBases,minSup) #构造FP-tree if myHead != None: mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList) #递归调用


 浙公网安备 33010602011771号
浙公网安备 33010602011771号