Stable Diffusion 学习笔记
对于diffusion的原始论文的理解
参考，https://www.bilibili.com/video/BV18a4y1T75X/?p=2&spm_id_from=pageDriver&vd_source=1eb6e5015a1f70daa97080d8ee786d5d
https://www.bilibili.com/video/BV1KC411Y7AF?p=2&vd_source=1eb6e5015a1f70daa97080d8ee786d5d
之前生成网络，GAN是主流算法，但是GAN有很多问题
当前生成网络的主流算法是diffusion
GAN的启发来着博弈论，
Diffusion的启发我觉得和雕塑很像，米开朗基罗说过，雕塑不是创造出新的东西，只是把多余的部分去掉
雕塑过程也是，先出大致轮廓，慢慢细化
Diffusion的过程也是这样，从一个随机noise，一步步的denoise，最终生成图片，所以，科学创新来源于生活和艺术
开始，
加噪的过程，forward，也是扩散过程
z是随机高斯噪音
α，是权重，开始原始图片的权重高，越往后加的噪音的权重越高
所以能得到，第T步，我得到的图片Xt的公式
这里的公式是，从Xt-1到Xt
可以推导出，从X0到Xt，不停代入可以推导出，
每一步都要产生随机噪声，从Xt到Xt-1为z1，从Xt-1到Xt-2为z2
这边要理解高斯分布的运算，
z1，z2符合高斯分布，他们乘上一个值，仍然符合高斯分布，只是方差需要变化
同样两个高斯分布相加后，仍然符合高斯分布，只是方差需要求和
最终可以得到X0到Xt的公式
那我们最终目的是，去噪
从标准高斯分布，通过diffusion模型，最终得到一个Q分布，一种数据分布，比如说是人脸，或苹果
从前面扩散过程，可以得到q(Xt|Xt-1)
逆向去噪，其实就是求q(Xt-1|Xt)，这个很难求解
这里一个思路，我用一个模型Pθ，来建模这个q，diffusion其实没有这么直接做
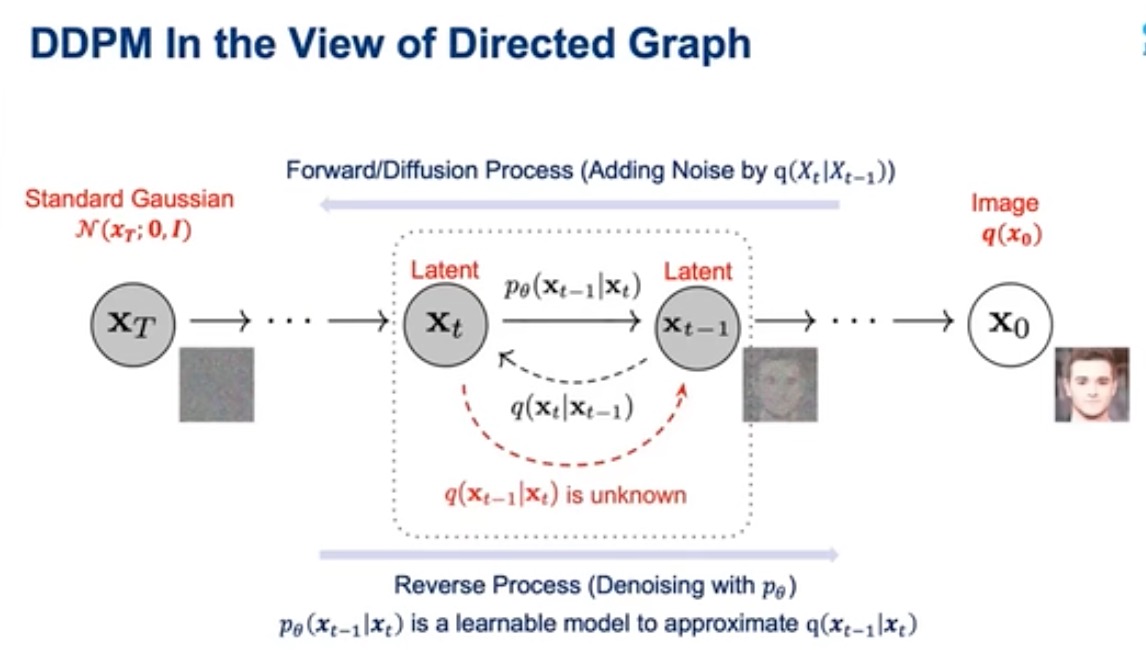
已知q(Xt|Xt-1)，求解q(Xt-1|Xt)，可以用贝叶斯公式
右边三项都是高斯分布，
高斯分布，本身式子如下，
exp，乘就是指数加，除就是指数减，得到
第一项，1-α=β，后面是α累乘，所以不能替换
这个式子展开，仍然是个高斯分布
为什么？你可以把高斯分布式子展开，和上面这个式子对应
从红色的这块，就是方差，这里可以看到方差是个常数，只有α和β
蓝色这块，是均值除方差，那我们方差已知，就可以代入求出均值，μt-1，式子里面写μt应该不对
好，现在均值和方差都有了，其实已经得到 q(Xt-1|Xt)分布，完成求解
但是这里有个问题，均值里面有X0，这个当前未知的
但是在扩散过程里面，我们已经有从X0到XT的式子，这里逆一下
然后代入，得到μt-1
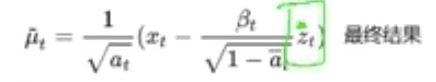
这里看到μt-1，只和Xt和Zt相关，
Zt是在第t步需要去掉的噪声，这个也是未知的
这里diffusion模型，用unet去学习和预测这个z
扩散的时候，是训练unet学习噪音，去噪的时候，每一步用unet去生成噪音
Unet，参考这篇https://www.bilibili.com/video/BV12F411x7cQ?p=3&vd_source=1eb6e5015a1f70daa97080d8ee786d5d
最早用于语义分割，即对于每个像素点进行分类，是人或不是
网络结构其实比较简单，encoder加上decoder
encoder，就是不断的通过cnn和pool进行下采样；decoder通过cnn和插值进行上采样
之所以叫Unet，是因为在encoder和decoder中，每一步产生的中间结果大小是对称一致的
并且这里会将中间结果进行拼接
总结一下，
训练过程，
2到4，是输入
x0，原始图片，从q分布里面采样一个，比如q分布都是人脸的图像
t，扩散步骤数，经过几步加噪到随机噪声
e，从标准正态分布中采样的一个噪声
5，对损失函数梯度下降
损失函数，
E，第t步的真实噪声
Eθ，Unet网络，θ是参数，
网络的输入是Xt和t，Xt通过上面的推导和用x0和噪声表达出；t，需要告诉网络当前是哪一步
网络的输出，预测第t步的误差
所以损失函数，就是真实误差-预测误差
5就是通过梯度下降让loss变小
生成过程，
1，从标准正态分布中采样一个噪声，Xt
2到5步，
由Xt，和Unet预测的噪声E，得到Xt-1的分布
从分布中随机采样一个作为Xt-1，如何采样
Xt-1的分布也是高斯分布，
从标准高斯分布采样一个随机值z，然后z*α + μ，乘方差加均值，就得到这个分布上的采样值
这就完成一步去噪声，迭代下去就可以得到X0
