SubQuery优化
https://zhuanlan.zhihu.com/p/60380557
子查询,分两种情况,
对于在From中的,称为‘derived table’,这种场景比较简单
对于在select,where中的,scalar表达式,这是主要要考虑的对象,因为这种情况cross了relational和scalar的处理

子查询,最关键的区分,是关联子查询(Correlated Subquery)和非关联子查询(Non-correlated Subquery)
关联子查询,子查询的执行,子查询参数,依赖于外层父查询输出的属性
非关联子查询,子查询的执行,不依赖于外层父查询的任何属性值,这样子查询具有独立性,可独自求解
非关联子查询的优化非常简单,因为可以独立求解,那就先求出并物化,带入父查询join即可
所以子查询优化的核心就是,去关联,de-correlate
从子查询返回的数据分类,
标量(Scalar-valued)子查询: 输出就是一个标量
存在性检测(Existential Test)子查询:特指 EXISTS 的子查询,返回一个布尔值
集合比较(Quantified Comparision)子查询:特指 IN、SOME、ANY 的查询,返回一个布尔值或Null,可能返回null


先看几篇基础的论文,
Microsoft的论文,
Parameterized Queries and Nesting Equivalencies - C Galindo-Legaria
Orthogonal Optimization of Subqueries and Aggregation - C Galindo-Legaria, M Joshi
Execution Strategies for SQL Subqueries - Mostafa Elhemali
Parameterized Queries and Nesting Equivalencies
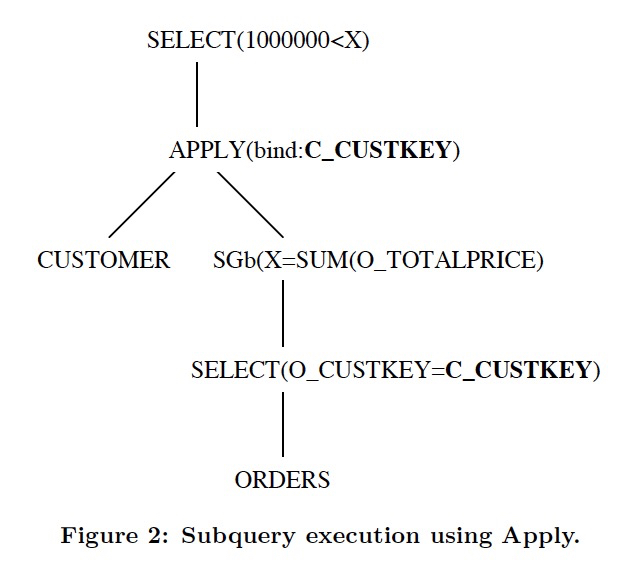
这篇论文核心,是提出Apply算子,并且如何通过各种规则,把Apply算子转换为普通的join
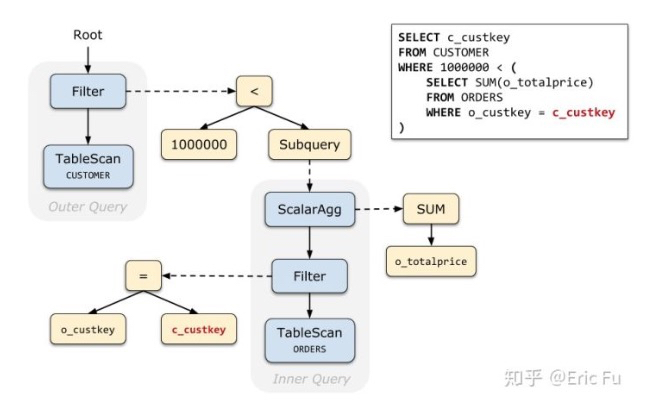
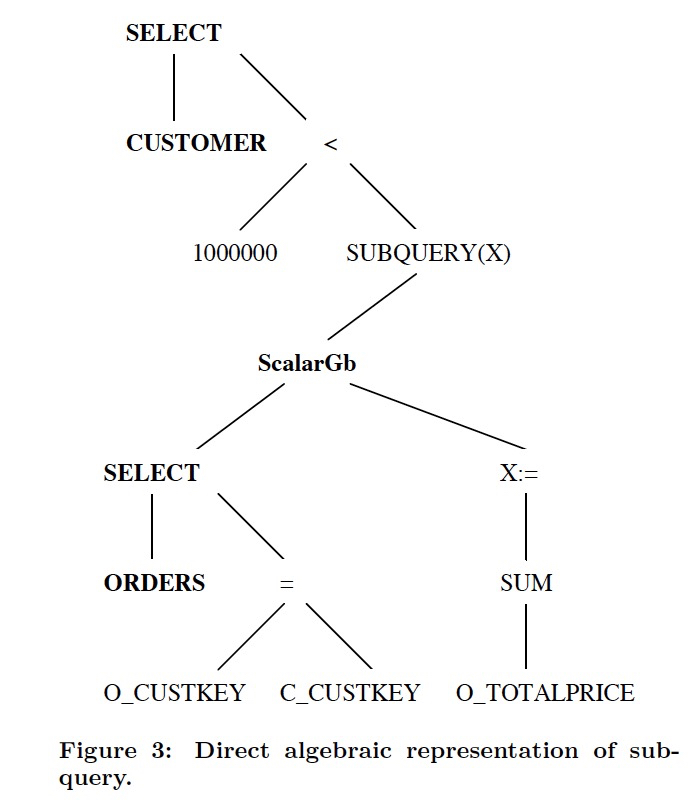
例子中一个,标量子查询的例子,
对于关联子查询,语义其实就是,对于outer表的每一行数据,都执行一遍子查询,这个非常类似,function programming里面的Apply算子
所以这里就是是用Apply算子来,描述这种关联性
Apply算子的定义,
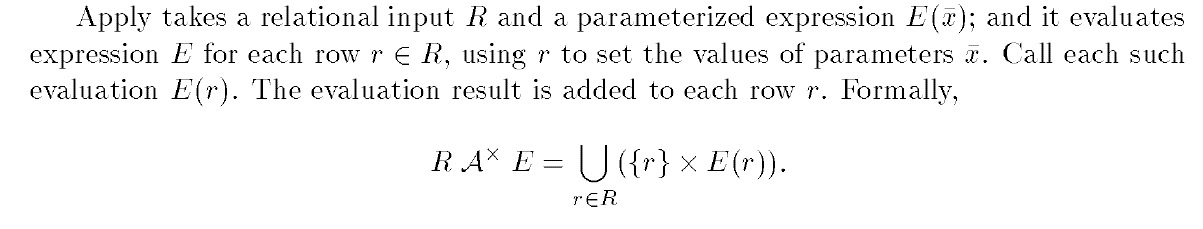
对于关系表R,其中每个r,带入E,因为E是个参数化expression,把结果求并集
这里其实对于R是要求Distinct,因为R中的r可能会重复,所以一般会加上一个算子去重
中间的A❌就代表apply算子,这里和普通join一样,根据对于E返回的Empty的处理,分为,

看上面的例子,用Apply算子的结果,
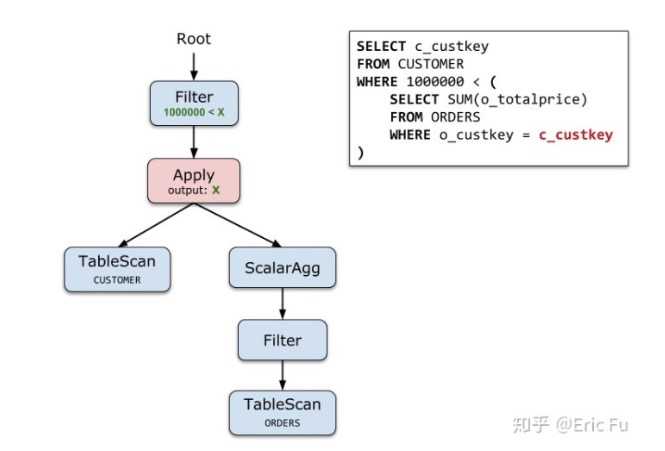
如果outer表足够小,并且有比较好的indexes的情况下,Correlatied执行效率也很好的
但是大多数一般情况下,Apply执行明显效率很低,所以要基于Apply算子去进行优化,Apply算子是个中间状态,比原来的形式更加容易使用关系代数优化
Apply的优化就,SubQuery unnesting或correlation removel,就是把Apply算子转换为regular join的过程,
下面看个最直接的例子,

Orthogonal Optimization of Subqueries and Aggregation
先看个例子,
标量,关联子查询的例子
最直接的方法,直接Correlated execution,不一定低效,如果Outer表很小,并且有适当的索引

80年代,提出过一些优化的方案,
比如,先Outerjoin,再aggregate的方案

或者,先Aggregate,再Join

但是这些方案,不是系统的方法论,不同的情况下,需要分析并使用不同的方法,
本文的方式是,把这些方法分解成,orthogonal, reusable primitives,用的时候可以组合起来,用cost-estimation的方式,评估到底使用哪些primitives
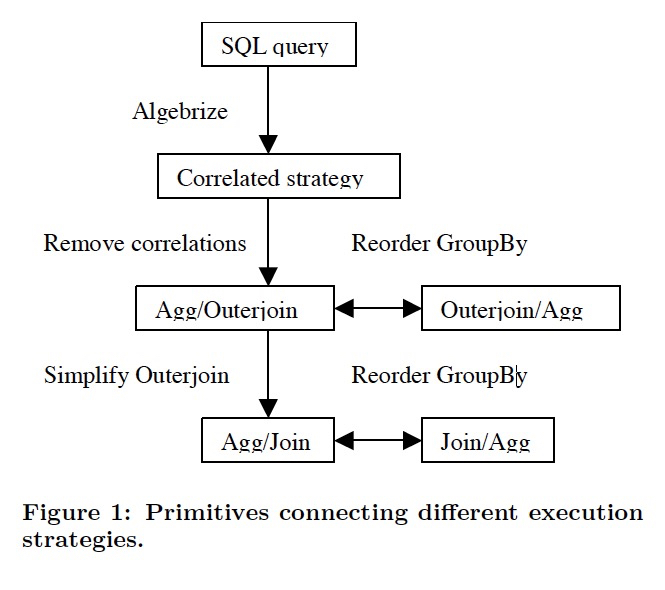
可以看出,分为图中的几步,下面分别解释一下各个步骤,
Algebrize
用Apply算子来抽象和替换parameterized execution of subexpressions
Apply算子的好处在于,去除relation和scalar节点间的mutual recursion
例子,左图,查询中有,scalar表达式,scalar表达式中又有子查询,所以执行的时候,需要反复在查询计划执行器和表达式执行器之间不断切换,效率很低,而且隔着scalar表达式,没法用关系代数进行优化或reorder
所以用Apply算子变换到右图,把子查询从scalar表达式中remove掉,放到关系代数树中
这里用标量子查询为例,但是其他的子查询也是一样的
这步只是对过程做了抽象,但实际上并没有改变执行计划
这里还提到一种,SegmentApply算子

可以认为是batch版本的Apply算子
因为我们可以用column A对R进行分组,对于每一组,table-valued,去调用E
a就是Distinct(A)
Remove Correlation
也就是remove apply
做法, 不断下推Apply,直到不关联了,转化为regular join
The process consists of pushing down Apply in the operator tree, towards the leaves, until the right child of Apply is no longer parameterized off the left child.
可以使用的转换rules,

(1) (2),左右不相干的情况下,apply可以直接转化成join
后面所有rules的目的,就是要转换成满足 (1) (2)
这里,(8)(9),比较难理解
首先,先看两个概念,

Vector Aggregation,GroupBY聚合,group by A,aggregate with Function F
关键,表为空的时候,返回也是empty
Scalar Aggregation,全局聚合,不指定A,aggregate with Function F
关键,总会有一行返回值,不会为empty;并且返回值和Aggregate函数相关,如果是sum,返回null,如果是count,返回0
(8)中,columns(R)表示join key,把group by提到外面后,需要先按照join key做group by
(8)和(9)的差别就是,(9)是Scalar Aggregation,所以返回值对于empty会出现null,所以F’需要特殊处理,用非null的column
再者Scalar Aggre提到外面后变成Vector Aggre (group by join key)
下面看个例子,仍然是上面的SQL

首先,为什么是Scalar Aggre,因为这里Group by join key,对于Apply算子,group by每次只apply到一个customer,所以是Scalar Aggre
用(9),把Scalar Aggre提出来,变成Vector Aggre
提出GroupBY后,剩下的可以直接应用(2)消除Apply
最后,由于最终的aggre结果需要非null,所以可以简化成inner join
Reorder Groupby
Groupby可以和其他算子进行交换,比如filter,join等
GroupBy的Reorder是否会降低cost,这个需要cost model去判断,比如先GroupBY,后Join,还是先Join,后GroupBy
GroupBy和Filter Reorder
条件,if and only if all the columns used in the filter are functionally determined by the grouping columns in the input relation
过滤的columns,由GroupBy columns决定
GroupBy和Join Reorder
GroupBy pushdown 条件,

GroupBy Pullup的条件,

Segmented Execution
以TPCH-17为例,
完成去关联后的计划如下,

这个计划的问题是,我们其实不用对所有Lineitem的rows都做这样的聚合过滤,其实只是需要对过滤后的PartKey对应的lineitem做

所以这里的方法是,把LineItem按照partkey进行group,每个group叫做Segment,然后对Segment执行子查询
叫做SegmentApply,
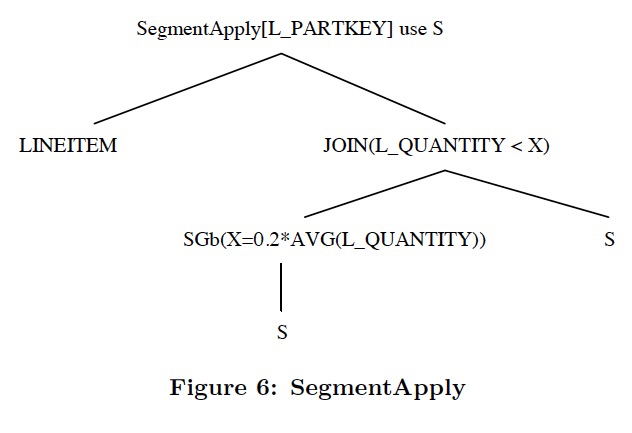
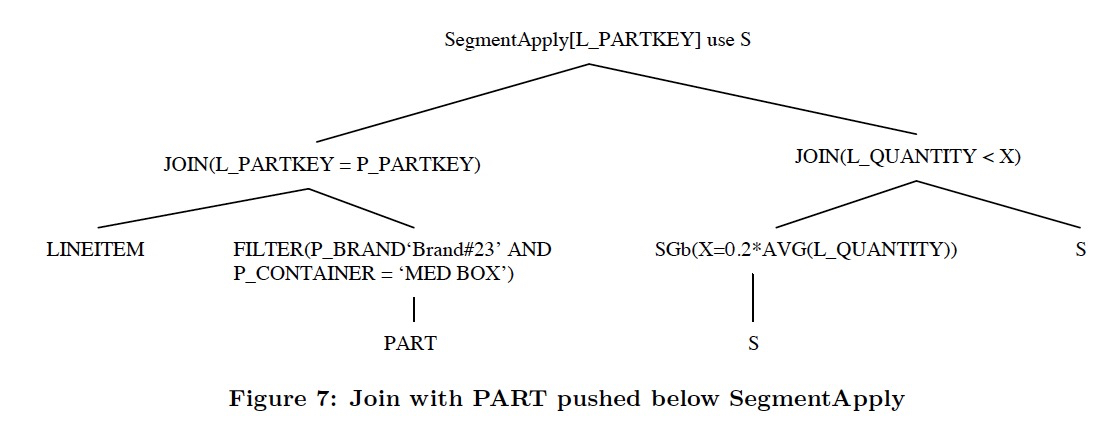
对于SegmentApply,下面要做的是,按照Part的条件过滤Segments,也就是要把外部的条件Push down到SegmentApply里面,
push down的条件是,segment的完整性,join的条件以segment为条件进行过滤,而不会过滤掉部分row


完成pushdown的结果如下,在SegmentApply之前,先会对LineItem做join进行过滤掉不需要的segment


 浙公网安备 33010602011771号
浙公网安备 33010602011771号