Hypothesis Testing

Refer to R Tutorial andExercise Solution

 

Researchers retain or reject hypothesis based on measurements of observed samples. The decision is often based on a statistical mechanism called hypothesis testing.

假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法。具体作法是：根据问题的需要对所研究的总体作某种假设，记作H0；选取合适的统计量，这个统计量的选取要使得在假设H0成立时，其分布为已知；由实测的样本，计算出统计量的值，并根据预先给定的显著性水平进行检验，作出拒绝或接受假设H0的判断。常用的假设检验方法有u—检验法、t—检验法、X2检验法、F—检验法，秩和检验等。

假设检验的基本思想是小概率反证法思想。小概率思想是指小概率事件（P<0.01或P<0.05）在一次试验中基本上不会发生。反证法思想是先提出假设(检验假设H0)，再用适当的统计方法确定假设成立的可能性大小，如可能性小,则认为假设不成立，若可能性大，则还不能认为假设成立。

 

Type I error 是指统计学中的一类错误，意思是本来是错误的结论却被接受了。TypeII error 是指统计学中的二类错误，也就是本来是正确的结论却被拒绝了。简而言之，就是存伪和弃真。

 

零假设(The null hypothesis), 是做统计检验时的一类假设。零假设的内容一般是希望成为正确的假设或者是需要着重考虑的假设.

与零假设相对的是备择假设（对立假设），即不希望看到的另一种可能。

 

Lower Tail Test of Population Mean with Known Variance (已知全局方差的全局平均值的下界检验)

The null hypothesis of the lower tail test of the population mean can be expressed as follows:

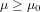
where μ₀ is a hypothesized lower bound of the true population mean μ.

假设检验, 首先是假设, 现在设定零假设为全局平均值的下界为u0

Let us define the test statistic z in terms of the sample mean, the sample size and the population standard deviation σ :

Then the null hypothesis of the lower tail test is to be rejected if z ≤−z_α , where z_α is the 100(1 − α) percentile of the standard normal distribution.

这个过程, 我们通过一个例子来看,

Problem

Suppose the manufacturer claims that the mean lifetime of a light bulb is more than 10,000 hours. In a sample of 30 light bulbs, it was found that they only last 9,900 hours on average. Assume the population standard deviation is 120 hours. At .05 significance level(显著性), can we reject the claim by the manufacturer?

厂商声明灯泡平均寿命为10000小时, 我们现在有一组测试数据, 30个测试灯泡, 测试平均寿命为9900, 全局方差为120, 要求在显著性0.05的情况下, 厂商的声明的假设是否成立.

这儿一定要谈显著性, 因为我们要区分出是抽样误差引起还是本质差别造成的, 当违反假设的case比例超出了我们设定的显著性, 那我们就不能认为这个是小概率事件, 而只能认为是假设根本不成立. 而在显著性范围内的case, 我们可以认为是由于抽样误差或其他小概率事件导致的, 并不影响该假设的成立.

这就和参数估计要谈confidence(置信度)一样, 值越小说明要求越严格.

Solution

The null hypothesis is that μ ≥ 10000. We begin with computing the test statistic.

> xbar = 9900            # sample mean 
> mu0 = 10000            # hypothesized value 
> sigma = 120            # population standard deviation 
> n = 30                 # sample size 
> z = (xbar−mu0)/(sigma/sqrt(n)) 
> z                      # test statistic 算出根据样本得出的统计值
[1] −4.5644

We then compute the critical value at .05 significance level.

> alpha = .05 
> z.alpha = qnorm(1−alpha) 
> −z.alpha               # critical value 满足正态分布的估计值
[1] −1.6449

Answer

The test statistic -4.5644 is less than the critical value of -1.6449. Hence, at .05 significance level, we reject the claim that mean lifetime of a light bulb is above 10,000 hours.

 

Upper Tail Test of Population Mean with Known Variance (上界检验)

The null hypothesis of the upper tail test of the population mean can be expressed as follows:

where μ₀ is a hypothesized upper bound of the true population mean μ.

Let us define the test statistic z in terms of the sample mean, the sample size and the population standard deviation σ :

Then the null hypothesis of the upper tail test is to be rejected if z ≥ z_α , where z_α is the 100(1 − α) percentile of the standard normal distribution.

 

Two-Tailed Test of Population Mean with Known Variance (双界检验)

The null hypothesis of the two-tailed test of the population mean can be expressed as follows:

where μ₀ is a hypothesized value of the true population mean μ.

Let us define the test statistic z in terms of the sample mean, the sample size and the population standard deviation σ :

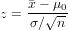
Then the null hypothesis of the two-tailed test is to be rejected if z ≤−z_α∕2 or z ≥ z_α∕2 , where z_α∕2 is the 100(1 − α∕2) percentile of the standard normal distribution.

 

Lower Tail Test of Population Mean with Unknown Variance

The null hypothesis of the lower tail test of the population mean can be expressed as follows:

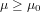
where μ₀ is a hypothesized lower bound of the true population mean μ.

Let us define the test statistic t in terms of the sample mean, the sample size and the sample standard deviation s :

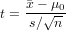
Then the null hypothesis of the lower tail test is to be rejected if t ≤−t_α , where t_α is the 100(1 − α) percentile of the Student t distribution with n − 1 degrees of freedom.

和已知全局方差不同就是:

1. 用sample standard deviation s来代替population standard deviation σ

2. 用Student t分布来代替正态分布

同样他也有上界和双界检验, 不笔记了

 

Lower Tail Test of Population Proportion (全局比例的下界检验)

The null hypothesis of the lower tail test about population proportion can be expressed as follows:

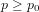
where p₀ is a hypothesized lower bound of the true population proportion p.

Let us define the test statistic z in terms of the sample proportion and the sample size:

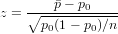
Then the null hypothesis of the lower tail test is to be rejected if z ≤−z_α , where z_α is the 100(1 − α) percentile of the standard normal distribution.

同样他也有上界和双界检验, 不笔记了

 

Type II Error

In hypothesis testing, a type II error is due to a failure of rejecting an invalid null hypothesis. The probability of avoiding a type II error is called the power of the hypothesis test, and is denoted by the quantity 1 - β .

Type II Error in Lower Tail Test of Population Mean with Known Variance

Problem

Suppose the manufacturer claims that the mean lifetime of a light bulb is more than 10,000 hours. Assume actual mean light bulb lifetime is 9,950 hours and the population standard deviation is 120 hours. At .05 significance level, what is the probability of having type II error for a sample size of 30 light bulb?

Solution

We begin with computing the standard deviation of the mean, sem.

> n = 30                # sample size 
> sigma = 120           # population standard deviation 
> sem = sigma/sqrt(n); sem   # standard error 
[1] 21.909

We next compute the lower bound of sample means for which the null hypothesis μ ≥ 10000 would not be rejected.

> alpha = .05           # significance level 
> mu0 = 10000           # hypothetical lower bound 
> q = qnorm(alpha, mean=mu0, sd=sem); q 
[1] 9964

Therefore, so long as the sample mean is greater than 9964 in a hypothesis test, the null hypothesis will not be rejected. Since we assume that the actual population mean is 9950, we can compute the probability of the sample mean above 9964, and thus found the probability of type II error.

> mu = 9950             # assumed actual mean 
> pnorm(q, mean=mu, sd=sem, lower.tail=FALSE) 
[1] 0.26196

Answer

If the light bulbs sample size is 30, the actual mean light bulb lifetime is 9,950 hours and the population standard deviation is 120 hours, then the probability of type II error for testing the null hypothesis μ ≥ 10000 at .05 significance level is 26.2%, and the power of the hypothesis test is 73.8%.