Treap平衡树
平衡树有splay,旋转treap,非旋转treap,而splay由于坑爹的6倍常数而不幸遭到dalao嫌弃(spaly:???),而非旋转treap经常被应用于可持久化数据结构中,蒟蒻表示不会
treap可以支持以下几种操作:插入,删除,查询x的排名(第几大),查询排名是x的数,x的前驱与后继
treap=tree+heap,即在树上用堆的形式进行维护,而这个堆的实现方式则是用rand随机出来的
除此之外,为了让操作更简便,可以定义数组记录子树大小和重复的数的数量
struct node { int l,r,val,siz,rnd,ct;//左子树,右子树,值,子树大小,随机数,子树中重复的数(x)的数目 }tree[100005];
1.更新当前节点子树大小
inline void update(int i)
{
tree[i].siz=tree[tree[i].l].siz+tree[tree[i].r].siz+tree[i].ct;//子树大小=左子树大小+右子树大小+重复的数的数量
}
2.左旋和右旋
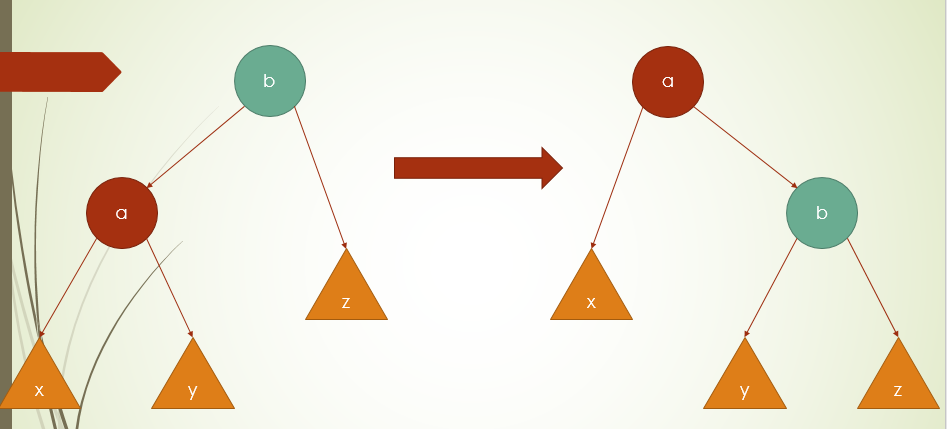
即不破坏平衡树性质的条件下旋转,直到随机值满足堆性质
图中右旋操作
把b作为a的右孩子,y作为b的孩子(左右取决于b有无左/右/左右孩子),y的父亲节点的孩子由b更新为a,实现提根操作
别忘了在旋转后要更新子树大小
左旋操作与右旋成镜面关系(所以这两个操作可以合并)(我太菜不会合并)
void lturn(int &i) { int t=tree[i].r; tree[i].r=tree[t].l; tree[t].l=i; tree[t].siz=tree[i].siz; update(i); i=t; } void rturn(int &i) { int t=tree[i].l; tree[i].l=tree[t].r; tree[t].r=i; tree[t].siz=tree[i].siz; update(i); i=t; }
3.插入与删除
从根节点开始,如果x小于当前节点值,则递归左儿子,否则右儿子
等于时,插入操作直接把当前节点ct值+1,若是空节点则新建节点
删除操作:(伪代码233)
if(ct>1)ct--
if(ct=1)
if(当前节点没有儿子)删除当前节点
if(有左儿子||有右儿子)用左儿子或右儿子替代该节点
if(有左右儿子)旋转直至出现上一种情况
void insert(int &i,int x) { if(i==0) { i=++node_num; tree[i].siz=tree[i].ct=1; tree[i].val=x; tree[i].rnd=rand(); return; } tree[i].siz++; if(tree[i].val==x)tree[i].ct++; else if(x>tree[i].val) { insert(tree[i].r,x); if(tree[tree[i].r].rnd<tree[i].rnd)lturn(i); } else { insert(tree[i].l,x); if(tree[tree[i].l].rnd<tree[i].rnd)rturn(i); } } void delete_(int &i,int x) { if(i==0)return; if(tree[i].val==x) { if(tree[i].ct>1) { tree[i].ct--; tree[i].siz--; } else { if(tree[i].l==0||tree[i].r==0) i=tree[i].l+tree[i].r; else if(tree[tree[i].l].rnd<tree[tree[i].r].rnd) { rturn(i); delete_(i,x); } else { lturn(i); delete_(i,x); } } } else if(x>tree[i].val) { tree[i].siz--; delete_(tree[i].r,x); } else { tree[i].siz--; delete_(tree[i].l,x); } }
4.查询x排名与查询排名x
根据排序二叉树,前者递归找到节点后查询左子树大小,后者根据x大小决定递归方向
int find_ranking(int i,int x) { if(i==0)return 0; if(tree[i].val==x)return tree[tree[i].l].siz+1; if(x>tree[i].val)return tree[tree[i].l].siz+tree[i].ct+find_ranking(tree[i].r,x); else return find_ranking(tree[i].l,x); } int find_num(int i,int x) { if(i==0)return 0; if(x<=tree[tree[i].l].siz)return find_num(tree[i].l,x); x-=tree[tree[i].l].siz; if(x<=tree[i].ct)return tree[i].val; x-=tree[i].ct; return find_num(tree[i].r,x); }
5.前驱与后继
递归当前数,记下递归路径上的最大最小值,max为前驱,min为后继
int find_pre(int i,int x) { if(i==0)return -inf; if(tree[i].val<x)return max(tree[i].val,find_pre(tree[i].r,x)); else if(tree[i].val>=x)return find_pre(tree[i].l,x); } int find_to(int i,int x) { if(i==0)return inf; if(tree[i].val<=x)return find_to(tree[i].r,x); else return min(tree[i].val,find_to(tree[i].l,x)); }
treap所有基本操作最高时间复杂度log2n,神(du)奇(liu)的数据结构~~~~~~~
蒟蒻代码:
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #define poi int using namespace std; const int inf=0x3fffffff; poi node_num,n,n_; struct node { poi l,r,val,siz,rnd,ct; }tree[100005]; inline poi rand() { static poi seed=2333; return seed=(poi)((((seed^998244353)+1926081711)*1989060411)%1000000007); } inline void update(poi i) { tree[i].siz=tree[tree[i].l].siz+tree[tree[i].r].siz+tree[i].ct; } void rturn(poi &i) { poi t=tree[i].l; tree[i].l=tree[t].r; tree[t].r=i; tree[t].siz=tree[i].siz; update(i); i=t; } void lturn(poi &i) { poi t=tree[i].r; tree[i].r=tree[t].l; tree[t].l=i; tree[t].siz=tree[i].siz; update(i); i=t; } void insert(poi &i,poi x) { if(i==0) { i=++node_num; tree[i].siz=tree[i].ct=1; tree[i].val=x; tree[i].rnd=rand(); return; } tree[i].siz++; if(tree[i].val==x)tree[i].ct++; else if(x>tree[i].val) { insert(tree[i].r,x); if(tree[tree[i].r].rnd<tree[i].rnd)lturn(i); } else { insert(tree[i].l,x); if(tree[tree[i].l].rnd<tree[i].rnd)rturn(i); } } void delete_(poi &i,poi x) { if(i==0)return; if(tree[i].val==x) { if(tree[i].ct>1) { tree[i].ct--; tree[i].siz--; } else { if(tree[i].l==0||tree[i].r==0) i=tree[i].l+tree[i].r; else if(tree[tree[i].l].rnd<tree[tree[i].r].rnd) { rturn(i); delete_(i,x); } else { lturn(i); delete_(i,x); } } } else if(x>tree[i].val) { tree[i].siz--; delete_(tree[i].r,x); } else { tree[i].siz--; delete_(tree[i].l,x); } } poi find_ranking(poi i,poi x) { if(i==0)return 0; if(tree[i].val==x)return tree[tree[i].l].siz+1; if(x>tree[i].val)return tree[tree[i].l].siz+tree[i].ct+find_ranking(tree[i].r,x); else return find_ranking(tree[i].l,x); } poi find_num(poi i,poi x) { if(i==0)return 0; if(x<=tree[tree[i].l].siz)return find_num(tree[i].l,x); x-=tree[tree[i].l].siz; if(x<=tree[i].ct)return tree[i].val; x-=tree[i].ct; return find_num(tree[i].r,x); } poi find_pre(poi i,poi x) { if(i==0)return -inf; if(tree[i].val<x)return max(tree[i].val,find_pre(tree[i].r,x)); else if(tree[i].val>=x)return find_pre(tree[i].l,x); } poi find_to(poi i,poi x) { if(i==0)return inf; if(tree[i].val<=x)return find_to(tree[i].r,x); else return min(tree[i].val,find_to(tree[i].l,x)); } int main() { scanf("%d",&n); for(poi j=1;j<=n;j++) { poi m,k; scanf("%d%d",&m,&k); if(m==1)insert(n_,k); if(m==2)delete_(n_,k); if(m==3)printf("%d\n",find_ranking(n_,k)); if(m==4)printf("%d\n",find_num(n_,k)); if(m==5)printf("%d\n",find_pre(n_,k)); if(m==6)printf("%d\n",find_to(n_,k)); } }
treap的用处更多的体现在与其他数据结构形成的更为优(du)美(liu)的算法中,所以这种基础数据结构要熟练掌握(线段树:兄弟你又加班了?)
蒟蒻第一次写blog,不足之处请各位dalao指出
转载随意(应该没人转吧)


