『POJ 3714』raid 题解 (平面最近点对)
原题链接(戳我)
思路:
第一次看到这道题时,相信不少人都会想到暴力枚举,但是一看数据范围: N = 100000
woc这题能做?
当然不能做也就基本不可能放到OJ上,于是乎我就开始在草稿纸上画了几个点:

Several minutes later...
woc这道题能做?(砸电脑)
当然砸电脑是不可能的,毕竟作为一个蒟蒻,心态不好点恐怕早就afo了呀
最后我还是没能靠自己想出来,于是乎在老师的怂恿之下,我默默地打开了百度,搜索了 平面最近点对
其实一开始,我是拒绝的,因为。。。看不懂
然鹅最后还是大概看懂了
大概是这么个意思:
运用分治的思想
先想办法把问题变小:
比如说用二分,找到中间点:

一刀下去,DUANG:
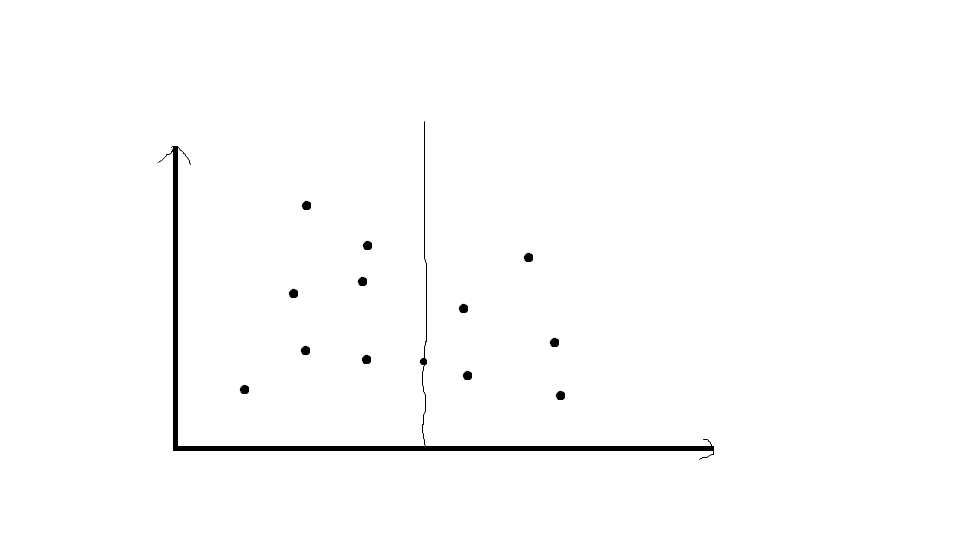
这个悲催的点集就变成两半了
然后继续切切切,到出现孤零零的一个点时:
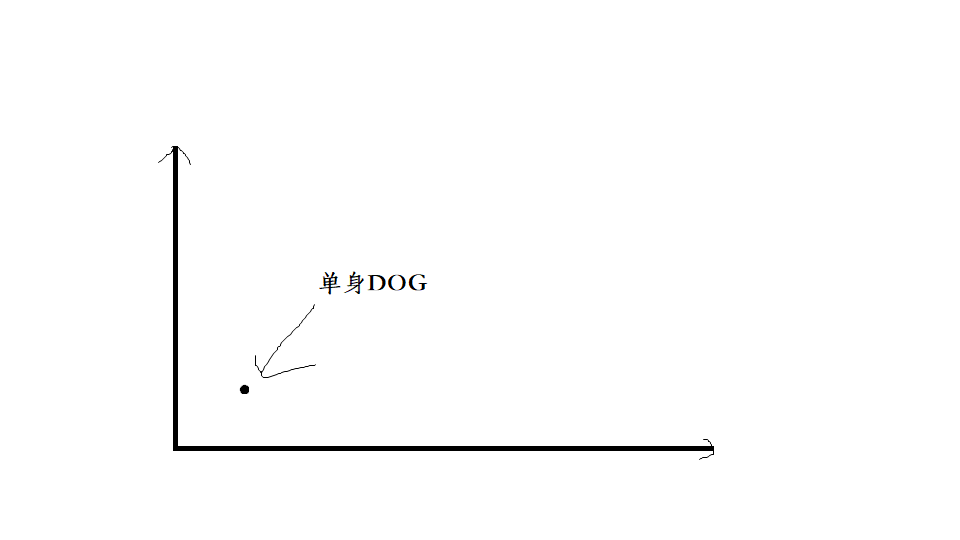
很明显这个可怜的点和我一样是条单身DOG(我好多朋友都有女票了QWQ),所以这个分治对它造成了极大值点伤害的暴击效果(没有点配对就不能得到距离)
于是乎我们就得到了第一个递归边界:
if(ll==rr) return BG;
如果切到最后,剩下了两个点的话:
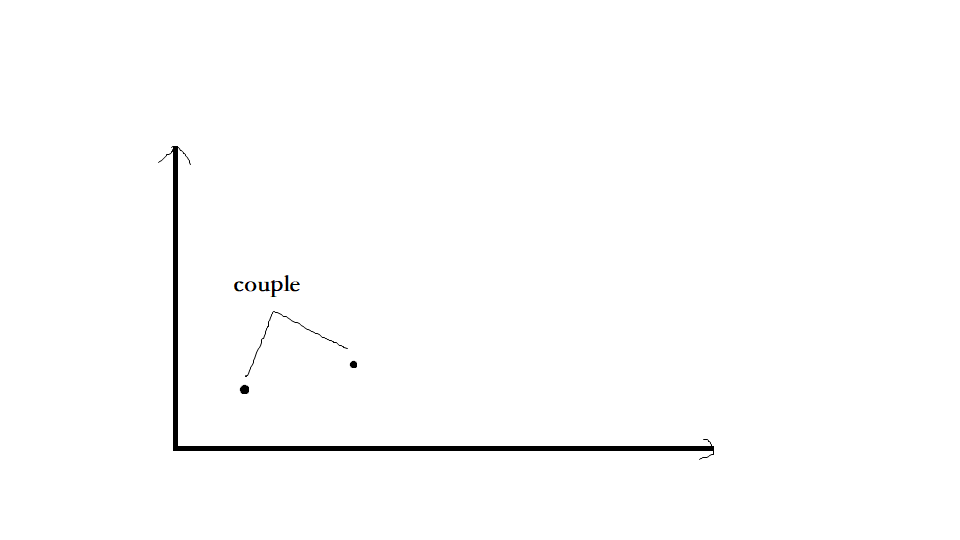
很明显这两个点就不再是single了
于是我们就返回它们之间的亲密值(距离),这就是第二个边界:
if(rr-ll==1) return get_dis(nd[ll],nd[rr]);
然后回到上一层,我们就能得到最优解。。。等等,有什么不对劲?
接下来就是重头戏了:
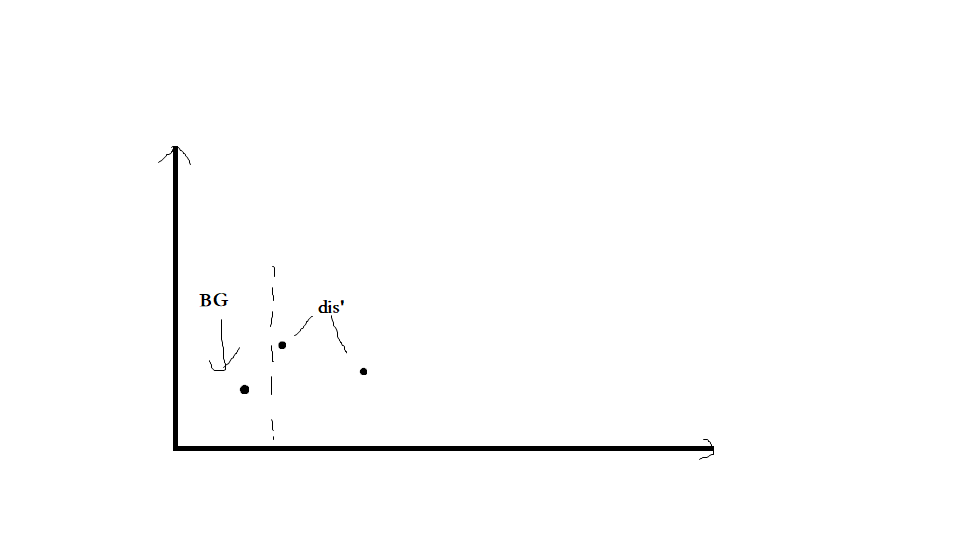
从图中我们很明显可以发现,一刀切下去后,两边分别求出各自的解,再从它们之中取最小值,这么做很明显是不对滴,
因为左边点和右边的偏左边那个点很明显要近很多
于是我们就想到了在左边和右边的点之中两个点两个点地枚举
但这太慢了,基本和直接暴力枚举没有什么区别
于是经过几分钟的思考(看题解)
我们想到了一个优化:
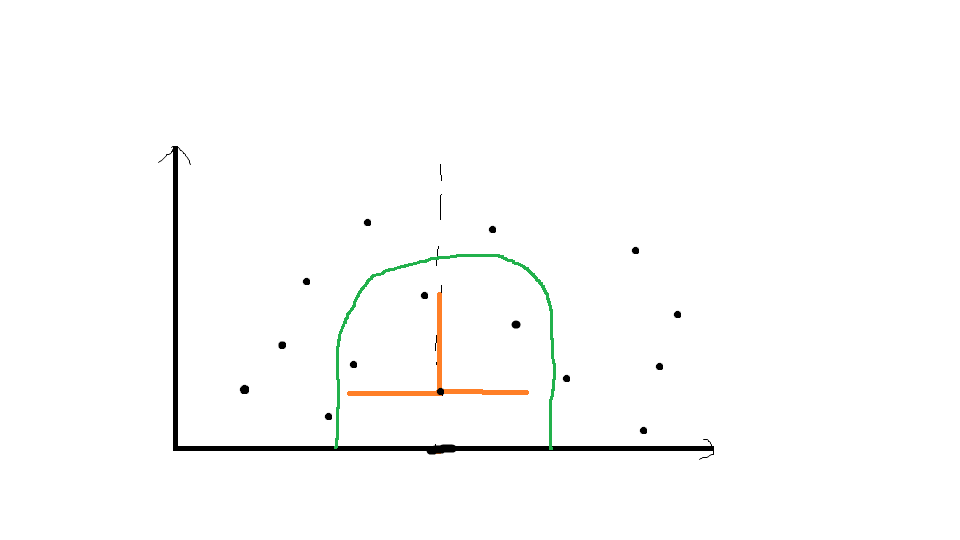
如果求出当前的最优解为橙线,那么很明显绿色区域以外的点都可以不去尝试了
但这样的话代码实现明显有点困难
于是乎我们就想到了先按照x坐标排序,先把距离差超过绿线的忽略掉,把绿线及以内的存入一个临时数组内:
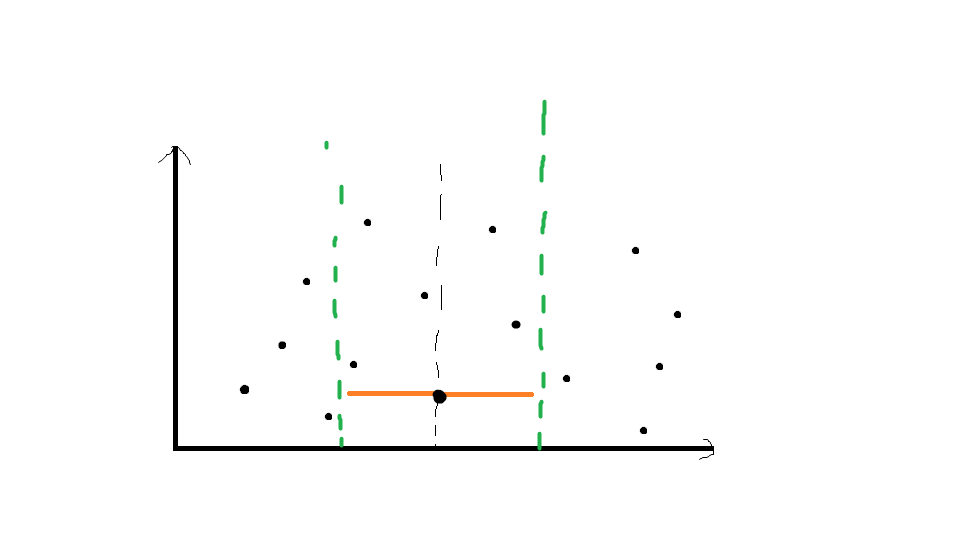
然后再把临时数组里的点按y坐标坐标排序,枚举点时,每当枚举到绿线以外时,我们都break掉,也就相当于忽略了绿线以外的点:
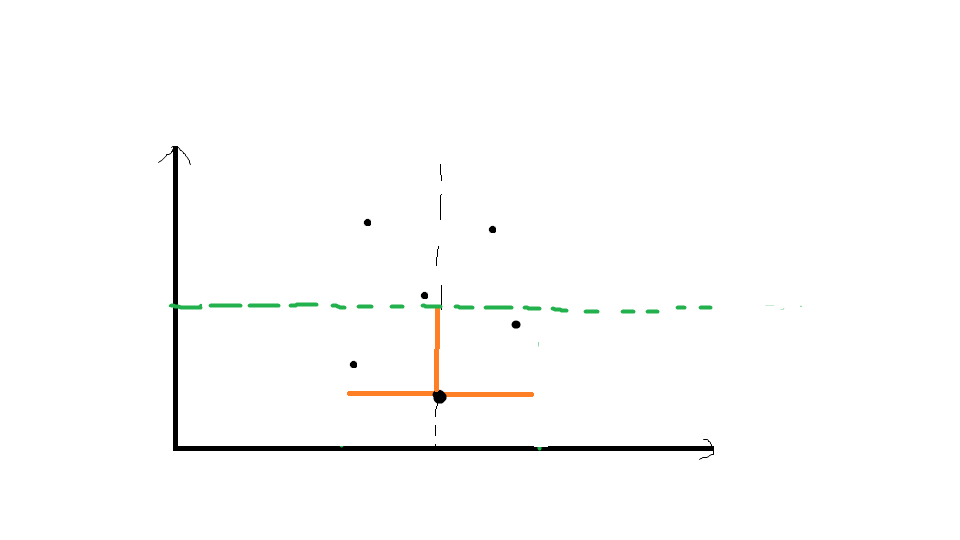
就这样,这一堆需要枚举的点就被我们减少到了3个
然后时间复杂度就噌噌噌地往下掉
至于这道题,我们通过题意可以知道,只有种类不同的点才用计算距离,于是乎我们在结构体里除了坐标外多加一个bool变量,代表点的种类:
struct node { double ii,jj; bool the_kind;//<--- }
然后每次进入求两点距离的get_dis函数的时候,如果两点种类相同,我们就直接返回极大值,这样的话如果一路走来都是同一种点,这份代码中的ans就会一直保持极大值,就会一直枚举左右两边组合的所有情况,这样就能保证代码的正确性
另外,听说还有更优秀的方法:就是按y坐标排序的时候利用上一次的排序结果,借用merge()来降低排序时间复杂度,这种我看得不是很懂,大家就自己问一问万能的度娘吧。
完整代码:
1 #include <cstdio> 2 #include <algorithm> 3 #include <cmath> 4 #define rg register 5 #define llint long long 6 #define usi unsigned 7 using namespace std; 8 const int N=1008611; 9 const double BG = 100861111111111.0; 10 11 struct node 12 { 13 double ii,jj; //该点的纵坐标ii,横坐标jj 14 bool the_kind; //该点的种类,0表示待攻击点,1代表特工 15 }nd[200002],tmp[200002]; 16 int t,n; //t组数据,n个待攻击点和n个agent 17 18 inline bool cmpx(node a,node b) //比较横坐标 19 { 20 return a.jj < b.jj; 21 } 22 inline bool cmpy(node a,node b) //比较纵坐标 23 { 24 return a.ii < b.ii; 25 } 26 inline double get_dis(node a,node b)//获得两点间距离 27 { 28 if(a.the_kind==b.the_kind) return BG;//两点种类相同,不计算距离 29 return sqrt((a.ii-b.ii)*(a.ii-b.ii)+(a.jj-b.jj)*(a.jj-b.jj)); 30 } 31 inline double divide_it(int ll,int rr) //分治求出当前子问题的解 32 { 33 if(ll==rr) return BG; //只有一个点,没有点来配对 34 if(rr-ll==1) return get_dis(nd[ll],nd[rr]);//只有两个点,将这两个点配对 35 int mid = (ll+rr)>>1;int cnt = 0;//求出中间点下标,并把可用点(可能更新当前最优答案的点)数置为零 36 double ans = min(divide_it(ll,mid),divide_it(mid+1,rr));//求出子问题的最优解 37 for(rg int i=ll;i<=rr;++i) //开始扫描,找到可用点(关于x坐标) 38 if(fabs(nd[i].jj-nd[mid].jj)<=ans) 39 ++cnt,tmp[cnt] = nd[i]; //把可用点存入临时数组内 40 sort(tmp+1,tmp+cnt+1,cmpy); //把可用点按照y轴坐标排个序 41 for(rg int i=1;i<cnt;++i) 42 for(rg int j=i+1;j<=cnt&&tmp[j].ii-tmp[i].ii<=ans;++j)//枚举可用点 43 { 44 double qwq = get_dis(tmp[i],tmp[j]);//两个点可能更新答案,计算距离 45 if(ans>qwq) ans = qwq; //更新 46 } 47 return ans; //返回最终结果 48 } 49 50 int main() 51 { 52 scanf("%d",&t); //t组数据 53 while(t--) 54 { 55 scanf("%d",&n); 56 for(rg int i=1;i<=n;++i) //输入待攻击点坐标 57 scanf("%lf%lf",&nd[i].jj,&nd[i].ii),nd[i].the_kind = 0; 58 int loopvar = n<<1; 59 for(rg int i=n+1;i<=loopvar;++i) 60 scanf("%lf%lf",&nd[i].jj,&nd[i].ii),nd[i].the_kind = 1; 61 sort(nd+1,nd+1+loopvar,cmpx);//按照x坐标排序 62 printf("%0.3f\n",divide_it(1,loopvar));//计算并输出结果 63 } 64 return 0; 65 }
这道题就这么愉快的地被我们切掉了
PS:卡了我3个小时的说QWQ,老是莫名其妙TLE
完成时间:2018/12/15 20:47



