1119 Pre- and Post-order Traversals (30 分)

题意

给出两个序列作为二叉树的先序序列和后序序列，序列内数字各不相同，判断是否能唯一确定一棵二叉树。输出任意一棵符合的二叉树的中序序列。

思路

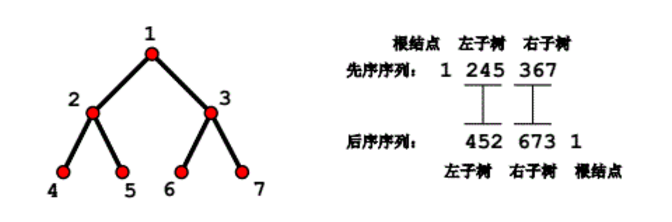
以上图为例进行说明，该图左的二叉树对应的先序序列和后序序列如该图右所示。

可以知道的一点是，先序序列的第一个结点和后序序列的最后一个结点都表示根结点，因此一定是相同的。对先序序列和后序序列的剩余部分，我们也可以知道两个序列都是先遍历左子树的所有结点、再遍历右子树的所有结点，并且两个序列的左子树结点个数相同、右子树结点个数也相同。此时，如果有中序序列的话，可以根据根结点在中序序列中的位置对左右子树进行区分。

那么，如果没有中序序列，又应该怎么区分左右子树呢？例如在这个例子中，如何在先序序列的剩余部分245367与后序序列的剩余部分452673中区分出左右子树？

由图中两个序列的分隔情况我们可以发现一个信息：先序序列的左子树部分245出现了2、4、5这三个数，而后序序列的左子树部分452也出现了2、4、5这三个数，虽然它们顺序不同，但出现的数字在排序后一定是一样的。

因此似乎可以这么做：从左往右等位扫描两个序列除去根结点的剩余部分(即先序序列的245367部分与后序序列的452673部分)，如果某个时候出现的数字在排序后是相同的，那么说明找到了其中一棵子树的全部结点。

但是这样做未免太繁琐，有没有更简单一些的做法呢？
这时我们就要用到最初提到的一点，即先序序列的第一个结点和后序序列的最后一个结点都表示根结点，它们一定是相同的。这个特点对于子树来说同样是成立的，即左(右)子树的先序序列第一个结点和左(右)子树的后序序列最后一个结点也是相同的。

因此我们可以在后序序列中寻找先序序列的第二个结点，后序序列中该结点的左侧(包含该结点)就是其中一棵子树的后序序列。例如在该例子中，先序序列的第二个结点是2，而在后序序列中同样也能找到值为2的结点，后序序列中在该结点的左侧(即452)就是其中一棵子树的后序序列。由此我们也可以获得这棵子树的结点个数为3，并以此得到该子树的先序序列为245。而原先序序列的剩余部分367就是另一棵子树的先序序列，原后序序列的剩余部分673就是另一棵子树的后序序列。

这样看起来问题似乎是解决了，但却忽视了很重要的一点，即如果其中一棵子树不存在，那么上面的过程是没有办法判断出存在的那棵子树到底是左子树还是右子树的。例如对下图的两棵二叉树来说，先序序列都是1234，后序序列都是3421，当我们由这两个序列确定根结点为1后，由上一段提出的方法，在后序序列中寻找先序序列的第二个结点(即2)，可以知道342是其中一棵子树的后序序列，这棵子树的结点个数为3，对应的先序序列为234，但是我们无法知道这到底是左子树还是右子树。事实上正是如此，当先序序列的第二个结点就是后序序列的倒数第二个结点时，说明只存在一棵子树，此时会产生不唯一性。只要存在一个结点的孩子个数为奇数，那么就是不唯一的；只有当所有结点的孩子个数均为偶数时，二叉树才唯一)

注意点

注意特判子树大小为\(1\)的情况。

const int N=35;
int pre[N],post[N];
int pos[N];
int n;
bool isunique=true;
vector<int> res;

void build(int prel,int prer,int postl,int postr)
{
    if(prel > prer) return;

    int root=pre[prel];
    if(prel == prer)
    {
        res.pb(root);
        return;
    }
    else
    {
        int k=pos[pre[prel+1]];
        if(k == postr-1) isunique=false;
        int leftLen=k-postl+1;
        build(prel+1,prel+leftLen,postl,k);
        res.pb(root);
        build(prel+leftLen+1,prer,k+1,postr-1);
    }
}

int main()
{
    cin>>n;

    for(int i=0;i<n;i++) cin>>pre[i];
    for(int i=0;i<n;i++) cin>>post[i],pos[post[i]]=i;

    build(0,n-1,0,n-1);

    if(isunique) puts("Yes");
    else puts("No");

    for(int i=0;i<res.size();i++)
        if(i) cout<<' '<<res[i];
        else cout<<res[i];
    cout<<endl;

    return 0;
}