1103 Integer Factorization (30 分)

不是很难吧，\(30\)分的题。

和1053 Path of Equal Weight (30 分)类似，毕竟都是\(DFS\)，^_^。

题意

给定正整数N、K、P，将N表示成K个正整数(可以相同，递减排列)的P次方的和，即\(N=n_1^P + \cdots + n_k^P\)，如果有多种方案，那么选择底数和\(n_1 +...+ n_k\)最大的方案；如果还有多种方案，那么选择底数序列的字典序最大的方案。

vector<int> ans;
vector<int> res;
int n,k,p;

void dfs(int u,int num,int psum,int sum)
{
    if(psum == n)
    {
        if(u == k)
        {
            if(sum > accumulate(ans.begin(),ans.end(),0) || res > ans)
                ans=res;
        }
        return;
    }

    for(int i=num;i>=1;i--)
    {
        LL t=1;
        for(int j=0;j<p;j++) t=t*i;
        if(psum + t > n) continue;

        res.push_back(i);
        dfs(u+1,i,psum+t,sum+i);
        res.pop_back();
    }
}

int main()
{
    cin>>n>>k>>p;

    dfs(0,n,0,0);

    if(ans.size() == 0) puts("Impossible");
    else
    {
        cout<<n<<" = ";
        for(int i=0;i<ans.size();i++)
            if(i) cout<<" + "<<ans[i]<<'^'<<p;
            else cout<<ans[i]<<'^'<<p;
        cout<<endl;
    }
    //system("pause");
    return 0;
}

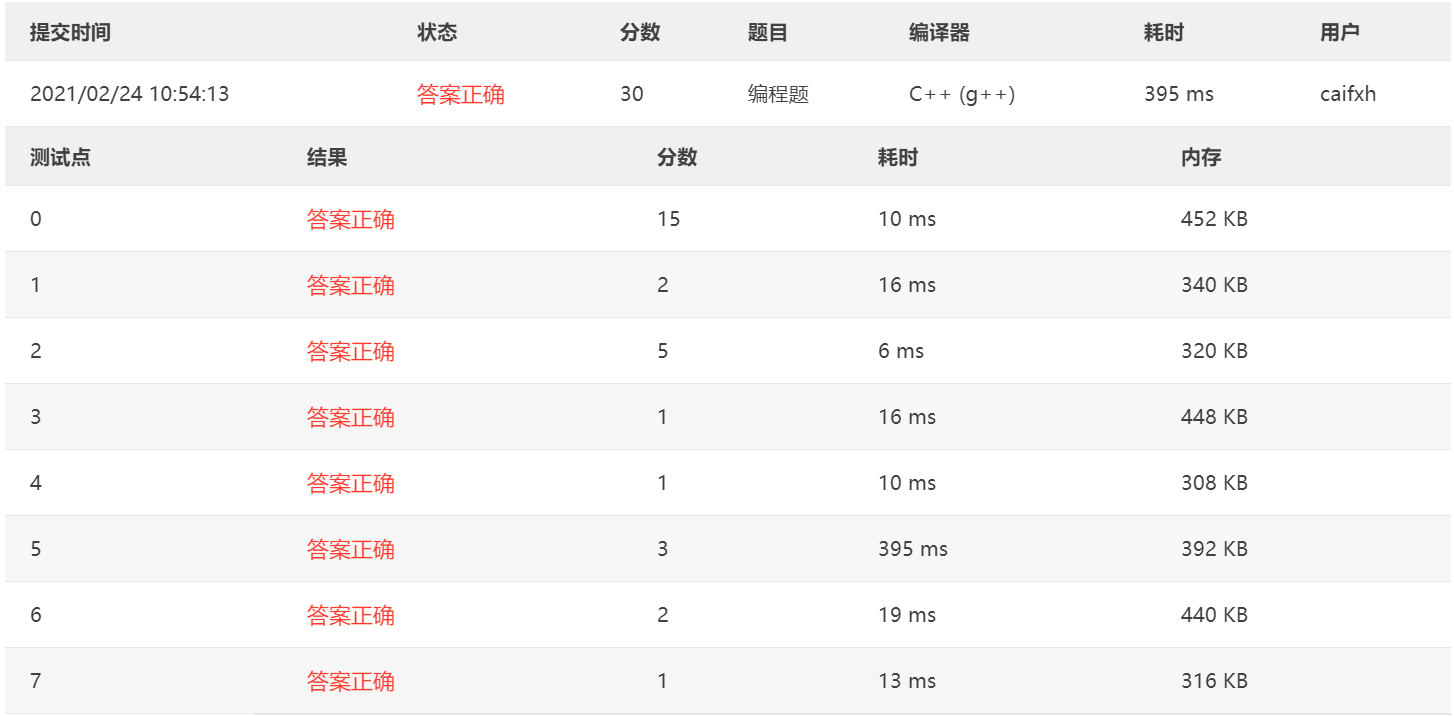
跑了\(900ms\)，有点吃紧。

以下为晴神思路：

1. 由于P不小于2，并且在单次运行中是固定的，因此不妨开一个vector fac，在输入P之后就预处理出所有不超过N的\(n^p\)。为了方便下标与元素有直接的对应，这里应把0也存进去。于是对N=10、P=2来说，fac[0]=0、fac[1]=1、fac[2]=4、fac[3]=9。
2. 接下来便是DFS函数。DFS用于从fac中选择若千个数(可以重复选)，使得它们的和等于N。于是需要针对fac 中的每个数，根据选与不选这个数来进入两个分支，因此DFS的参数中必须有:①当前处理到的是fac的几号位，不妨记为index；②当前已经选择了几个数，不妨记为nowK。由于目的是选出的数之和为N，因此参数中也需要记录当前选择出的数之和sum。而为了保证有多个方案时底数之和最小，还需要在参数中记录当前选择出的数的底数之和facSum。于是需要的参数就齐全了。
   此外，还需要开一个vector ans，用来存放最优的底数序列，而用一个 vector temp来存放当前选中的底数组成的临时序列。
3. 考虑递归本身。注意：为了让结果能保证字典序大的序列优先被选中，让index从大到小递减来遍历，这样就总是能先选中fac中较大的数了。显然，如果当前需要对fac[index]进行选择，那么就会有“选”与“不选”两种选择。如果不选，就可以把问题转化为对fac[index-1]进行选择，此时nowK、sum、facSum 均不变；而如果选，由于每个数字可以重复选择，因此下一步还应当对fac[index]进行选择，但由于当前选了fac[index]，需要把底数index加入当前序列temp中，同时让nowK加1、sum加上fac[index]、facSum 加上index。显然，DFS必须在index不小于1时执行，因为题目求的是正整数的幂次之和。
4. 那么，递归到什么时候停止呢?首先，如果到了某个时候sum== N并且nowK == k成立，那么说明找到了一个满足条件的序列(就是temp，注意保存的是底数)，此时为了处理多方案的情况，需要判断底数之和facSum是否比一个全局记录的最大底数之和maxFacSum更大，若是，则更新maxFacSum，并把temp赋给ans。除此之外，当sum>N或者nowK>K时，不可能会产生答案，可以直接返回。

注意点

1. 多方案时判断是否更优的做法的时间复杂度最好是\(O(1)\)，否则容易超时。因此必须在DFS的参数中记录当前底数之和facSum，避免在找到一组解时计算序列的底数之和。
2. 同①，不要在找到一组解时才判断temp序列与ans序列的字典序关系，而应该让index从大到小进行选择，这样fac[index]大的就会相对早地被选中。

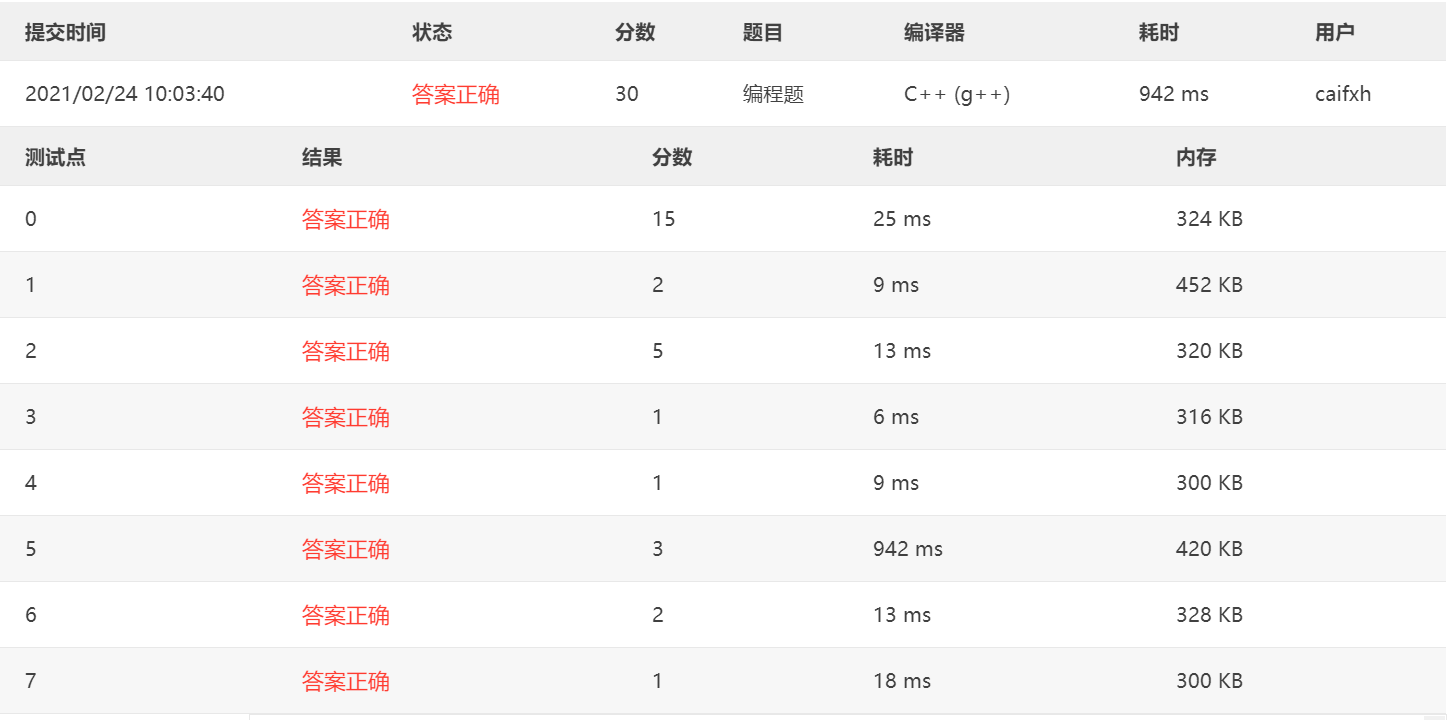
以下为优化后的代码，快了一倍多。

const int N=410;
vector<int> ans;
vector<int> res;
int ansSum;
int apow[N];
int n,k,p;
int st;

void init()
{
    for(int i=0;;i++)
    {
        apow[i]=1;
        for(int j=0;j<p;j++) apow[i]*=i;
        if(apow[i] > n)
        {
            st=i-1;
            break;
        }
    }
}

void dfs(int u,int num,int psum,int sum)
{
    if(psum > n || u > k) return;
    
    if(psum == n)
    {
        if(u == k)
        {
            if(sum > ansSum)
                ans=res, ansSum=sum;
        }
        return;
    }

    for(int i=num;i>=1;i--)
    {
        res.push_back(i);
        dfs(u+1,i,psum+apow[i],sum+i);
        res.pop_back();
    }
}

int main()
{
    cin>>n>>k>>p;
    
    init();

    dfs(0,st,0,0);

    if(ans.size() == 0) puts("Impossible");
    else
    {
        cout<<n<<" = ";
        for(int i=0;i<ans.size();i++)
            if(i) cout<<" + "<<ans[i]<<'^'<<p;
            else cout<<ans[i]<<'^'<<p;
        cout<<endl;
    }
    //system("pause");
    return 0;
}