1021 Deepest Root (25分)

一眼树的直径。

题意

给出N个结点与N-1条边，问：它们能否形成一棵N个结点的树？如果能，则从中选出结点作为树根，使得整棵树的高度最大。输出所有满足要求的可以作为树根的结点。

思路

当图连通时，由于题目保证只有N-1条边，因此一定能确定是一棵树，下面的任务就是选择合适的根结点，使得树的高度最大。具体做法为：先任意选择一个结点，从该结点开始遍历整棵树，获取能达到的最深的顶点(记为结点集合A)；然后从集合A中任意一个结点出发遍历整棵树，获取能达到的最深的顶点(记为结点集合B)。这样集合A与集合B的并集即为所求的使树高最大的根结点。

证明过程如下(第一步证明最重要)：

第一步，证明从任意结点出发进行遍历，得到的最深结点一定是所求根结点集合的一部分。已知一棵树的使树高最大的根结点为R，那么存在某个叶子结点L，使得从R到L的长度即为树的最大树高(显然，R与L同为所求根结点集合的一部分)。这里把R和L的路径拉成一条直线(称为树的直径，下同)，如图10-4所示，从某个结点X开始进行遍历(图中省略了不必要的结点，以线段的概念长度代表结点之间的距离，下同)。假设遍历得到的最深结点是Y，而Y既不是R也不是L，那么一定有OY>OL成立，于是有RO+OY> RO+OL成立，因此结点Y才是以R为根结点的产生最大树高的叶子结点，而这违背了之前给定的前提(R到L的长度是树的最大树高)，因此假设(遍历得到的最深结点Y既不是R也不是L)不成立，由此得出结论：从任意结点X进行树的遍历，得到的最深结点定是R或者L,即所求根结点集合的一部分。

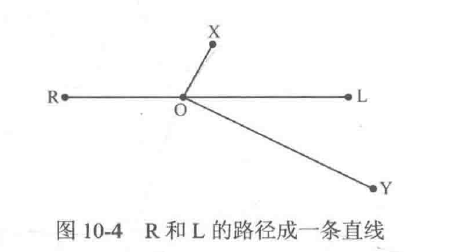
第二步，证明所有直径一定有一段公共重合区间(或是交于一个公共点)。

先证明任意两条直径一定相交。假设存在两条不相交的直径X-Y与W- Z(长度相同)，如图10-5所示。由于树是连通的结构，因此在X-Y中一-定存在一点P，在W-Z中一定存在一点Q，使得PQ是互相可以到达的。这样就可以利用P-Q拼接出一条更长的直径，而这与X- Y、W-Z是两条不相交的直径矛盾，因此假设不成立，任意两条直径一定相交。

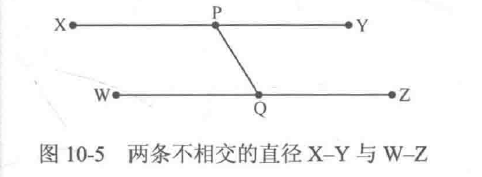
再证明所有直径一定有一段公共重合区间或一个公共点。

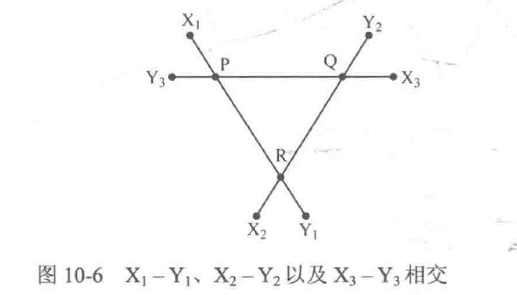
假设3条直径$X_1-Y_1$、$X_2- Y_2$以及$X_3- Y_3$相互相交，但不交于同一点(设交点分别为P、Q、R)，如图10-6所示。显然可以通过P、Q、R来拼接出更长的直径(例如$X_1-P-Q-R- Y_1$比$X_1一Y_1$长)，因此假设不成立。公共重合区间的证明同理。因此所有直径一-定有一段公共重合区间或一个公共点，形成类似于图10-7的结构，其中$A_1 \sim A_m$与$B_1 \sim B_k$为所有直径的端点，且$A_1 \sim A_m$与结点P的距离相等，$B_1 \sim B_k$与结点Q的距离相等，直径为$A1 \sim A_m$到达$B_1 \sim B_k$的任意组合。

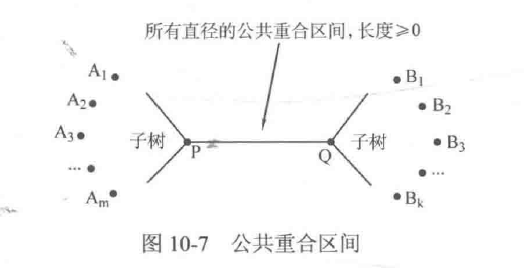
第三步，证明两次遍历结果的并集为所求的根结点集合。

若第一次遍历选择的初始结点在PQ之间，则最深结点显然是$A_1 \sim A_m$或者$B_1 \sim B_k$中的其中一组(或者全部)，而在第二次遍历时任取一个根结点即可遍历完整另外一侧的所有最深结点。同理，若第一次遍历选择的初始结点在P的左侧。(或Q的右侧)，那么最深结点一定是$B_1 \sim B_k$(或$A_1 \sim A_m$)，这样在第二次遍历时任取一个根结点同样可以遍历完整另外侧的所有最深结点，命题得证。

注意点

和树的直径的模板题不同的是要求出所有能够构成直径两个端点的点，即为最深的根。

注意对$n=1$的特殊处理，这个corner case还是挺好想的，第一次交$23$分，调试一下就发现了。

由于要从小到大输出所有最深的根，故将它们全部插入集合中输出。

连通分量直接dfs统计就行，需要一个判重数组，也可以并查集。

const int N=10010;
vector<int> g[N];
vector<int> node;
int d[N];
bool vis[N];
int n;
int far;
set<int> S;
 
void dfs(int u,int fa)
{
    vis[u]=true;
    for(int i=0;i<g[u].size();i++)
    {
        int j=g[u][i];
        if(j == fa) continue;
        if(!vis[j])
        {
            d[j]=d[u]+1;
            if(d[j] > d[far])
            {
                node.clear();
                node.pb(j);
                far=j;
            }
            else if(d[j] == d[far])
                node.pb(j);
    
            dfs(j,u);
        }
    }
}
 
int main()
{
    cin>>n;
 
    for(int i=0;i<n-1;i++)
    {
        int a,b;
        cin>>a>>b;
        g[a].pb(b);
        g[b].pb(a);
    }
 
    int cnt=0;
    for(int i=1;i<=n;i++)
        if(!vis[i])
        {
            dfs(i,-1);
            if(i == 1)
            {
                if(!node.size()) node.pb(1);//corner case
                for(int i=0;i<node.size();i++) S.insert(node[i]);
            }
            cnt++;
        }
    
    if(cnt >= 2) printf("Error: %d components\n",cnt);
    else
    {
        d[far]=0;
        node.clear();
        memset(vis,0,sizeof vis);
        dfs(far,-1);
        for(int i=0;i<node.size();i++) S.insert(node[i]);
 
        for(auto t:S) cout<<t<<endl;
    }
 
    //system("pause");
    return 0;
}

并查集

const int N=10010;
vector<int> g[N];
vector<int> node;
int d[N];
int p[N];
int n;
int far;
set<int> S;
 
int find(int x)
{
    if(x != p[x]) p[x]=find(p[x]);
    return p[x];
}
 
void dfs(int u,int fa)
{
    for(int i=0;i<g[u].size();i++)
    {
        int j=g[u][i];
        if(j == fa) continue;
 
        d[j]=d[u]+1;
        if(d[j] > d[far])
        {
            node.clear();
            node.pb(j);
            far=j;
        }
        else if(d[j] == d[far])
            node.pb(j);
 
        dfs(j,u);
    }
}
 
int main()
{
    cin>>n;
    
    for(int i=1;i<=n;i++) p[i]=i;
 
    for(int i=0;i<n-1;i++)
    {
        int a,b;
        cin>>a>>b;
        g[a].pb(b);
        g[b].pb(a);
        int pa=find(a),pb=find(b);
        p[pa]=pb;
    }
 
    int cnt=0;
    for(int i=1;i<=n;i++) 
        if(p[i] == i)
            cnt++;
            
    if(cnt >= 2) printf("Error: %d components\n",cnt);
    else
    {
        dfs(1,-1);
        if(!node.size()) node.pb(1);
        for(int i=0;i<node.size();i++) S.insert(node[i]);
        
        d[far]=0;
        node.clear();
        
        dfs(far,-1);
        for(int i=0;i<node.size();i++) S.insert(node[i]);
 
        for(auto t:S) cout<<t<<endl;
    }
 
    //system("pause");
    return 0;
}