《算法笔记》——第十三章 树状数组学习记录
lowbit运算
众所周知,二进制有很多奇妙的应用,这里介绍其中非常经典的一个,也就是lowbit 运算,即lowbit(x)=x&(-x)。
那么这个式子是什么意思呢?先来看x从二进制的角度发生了什么。从《计算机组成原理》中可以知道,整数在计算机中一般采用的是补码存储,并且把一个补码表示的整数x变成其相反数-x的过程相当于把x的二进制的每一位都取反,然后末位加1。而这等价于直接把x的二进制最右边的1左边的每一位都取反。通过它可以很容易推得lowbit(x)=x & (-x)就是取x的二进制最右边的1和它右边所有0,因此它一定是2的幂次,即1、2、4、8等。显然,lowbit(x)也可以理解为能整除x的最大2的幂次。
树状数组及其应用
先来看一个问题:给出一个整数序列A,元素个数为N (\(N≤10^5\)),接下来查询K次(\(K≤10^5\)),每次查询将给出一个正整数x(x≤N),求前x个整数之和。假设在查询的过程中可能随时给第x个整数加上一个整数v,要求在查询中能实时输出前x个整数之和(更新操作和查询操作的次数总和为K次)。
树状数组(Binary Indexed Tree, BIT)。它其实仍然是一个 数组,并且与sum数组类似,是一个用来记录和的数组,只不过它存放的不是前i个整数之和,而是在i号位之前(含i号
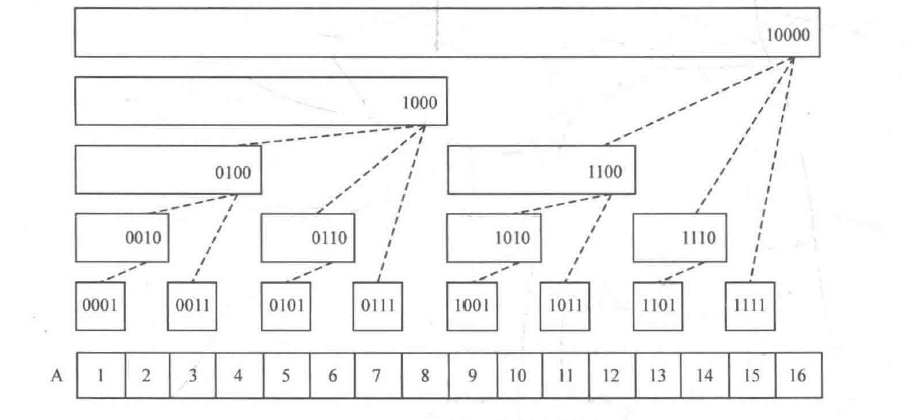
位,下同) lowbit(i)个整数之和。如图所示,数组A是原始数组,有A[1] ~ A[16]共16个元素;数组C是树状数组,其中C[i]存放数组A中i号位之前lowbit(i)个元素之和(请不要陷入二进制过深,本节将尽可能减少二进制的出现,希望能使树状数组的讲解更清晰)。显然,C[i]的覆盖长度是lowbit(i)(也可以理解成管辖范围),它是2的幂次,即1、2、4、8等。
需要注意的是,树状数组仍旧是一个平坦的数组,画成树形是为了让存储的元素更容易观察。
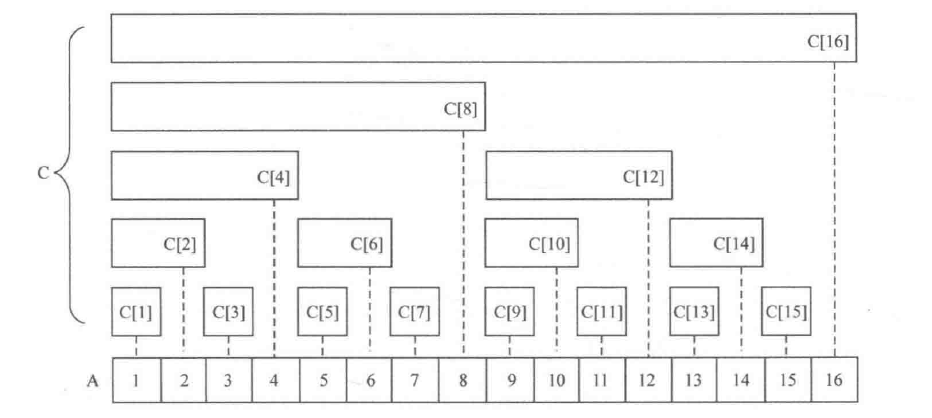
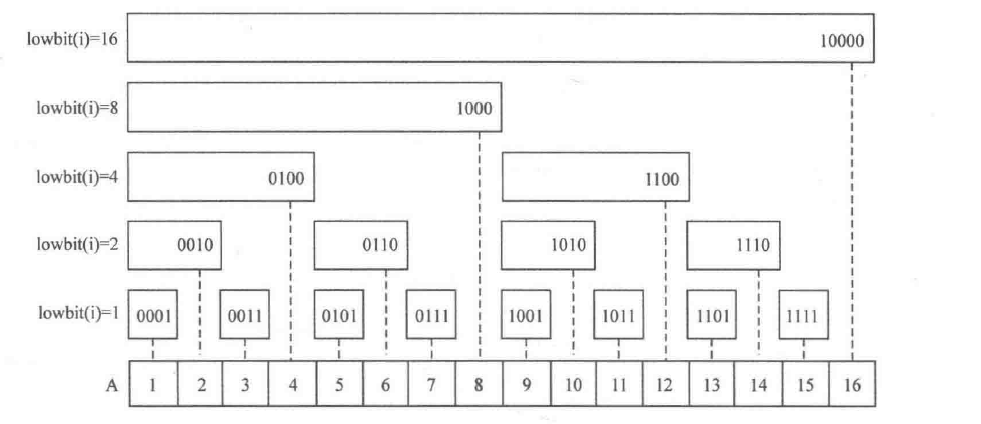
- C[1]=A[1](长度为lowbit(1)= 1)
- C[2]= A[1] +A[2](长度为lowbit(2)= 2)
- C[3]= A[3](长度为lowbit(3)= 1)
- C[4]= A[1]+ A[2]+ A[3]+ A[4](长度为lowbit(4)= 4)
- C[5]= A[5](长度为lowbit(5)= 1)
- C[6]= A[5]+ A[6](长度为lowbit(6)= 2)
- C[7]= A[7](长度为lowbit(7)= 1)
此处强调,树状数组的定义非常重要,特别是“C[i]的覆盖长度是lowbit(i)” 这点;另外,树状数组的下标必须从1开始,请读者务必注意。接下来思考一下,在这样的定义下,怎样解决下面两个问题,也就是本节一开始提出的问题:
- 设计函数getSum(x),返回前x个数之和A[1] +... + A[x]。
- 设计函数update(x,v),实现将第x个数加上一个数v的功能,即A[x] +=v。
先来看第一个问题,即如何设计函数getSum(x),返回前x个数之和。不妨先看个例子。假设想要查询A[1] +..+ A[14],那么从树状数组的定义出发,它实际是什么东西呢?很容易发现A[1] +...+ A[14]= C[8]+C[12]+C[14]。又比如要
查询A[1] +... +A[11],从图中同样可以得到A[1] +...+ A[11]= C[8]+C[10]+C[11]。那么怎样
知道A[1] +...+ A[x]对应的是树状数组中的哪些项呢?事实上这很简单。
记SUM(1,x)= A[1]+...+ A[x],由于C[x]的覆盖长度是lowbit(x),因此C[x]= A[x - lowbit(x)+ 1]+...A[x]
于是马上可以得到SUM(1,x) = A[1]+...+A[x]=A[1]+..+ A[x - lowbit(x)]+ A[x-lowbit(x)+1]+..+A[x]
= SUM(1,x - lowbit(x))+ C[x]
这样就把SUM(1, x)转换为SUM(1, x - lowbit(x))了。
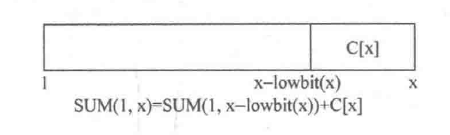
显然,由于lowbit(i)的作用是定位i的二进制中最右边的1,因此i= i- lowbitti)事实上是不断把i的二进制中最右边的1置为0的过程。所以getSum函数的for循环执行次数为x的二进制中1的个数,也就是说,getSum 函数的时间复杂度为O(logN)。从另一个角度理解,getSum 函数的过程实际上是在沿着一条不断左上的路径行进(再次强调,不要过深陷入图中的二进制,因为这与理解getSum函数没有关系)。于是由于“树”高是O(logN)级别,因此可以同样得到getSum函数的时间复杂度就是O(logN)。另外,如果要求数组下标在区间[x, y]内的数之和,即A[x] + A[x+ 1] +...+ A[y],可以转换成getSum(y)- getSum(x- 1)来解决,这是一个很重要的技巧。
int sum(int x)
{
int res=0;
for(int i=x;i;i-=lowbit(i))
res+=c[i];
return res;
}
接着来看第二个问题,即如何设计函数update(x,v),实现将第x个数加上一个数v的功能。
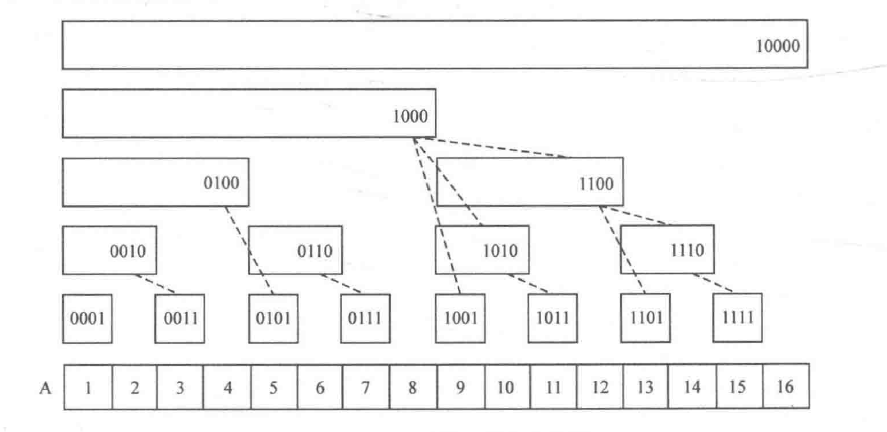
来看两个例子。假如要让A[6]加上一个数v,那么就要寻找树状数组C中能覆盖了A[6]的元素,让它们都加上v。也就是说,如果要让A[6]加上v,实际上是要让C[6]、C[8]、C[16]都加上v。同样,如果要将A[9]加上一个数v,实际上就是要让C[9]、C[10]、C[12]、C[16]都加上v。于是问题又来了一想要给 A[x]加上v时,怎样去寻找树状数组中的对应项呢?
在上一段中已经说过,要让A[x]加上v,就是要寻找树状数组C中能覆盖A[x]的那些元素,让它们都加上v。只需要总是寻找离当前的“矩形”C[x]最近的“矩形”C[y],使得C[y]能够覆盖C[x]即可。例如要让A[5]加上v,就从C[5]开始找起:离C[5]最近的能覆盖C[5]的“矩形”是C[6],离C[6]最近的能覆盖C[6]的“矩形”是C[8],而离C[8]最近的能覆盖C[8]的“矩形”是C[16],于是只要把C[5]、C[6]、 C[8]、 C[16]都加上v即可。
那么,如何找到距离当前的C[x]最近的能覆盖C[x]的C[y]呢?首先,可以得到一个显然的结论:lowbit(y)必须大于lowbit(x)(不然怎么覆盖.......)。于是问题等价于求一个尽可能小的整数a,使得lowbit(x+a)> lowbit(x)。 显然,由于lowbit(x)是取x的二进制最右边的1的位置,因此如果lowbit(a) < lowbit(x),lowbit(x + a)就会小于lowbit(x)。为此lowbit(a)必须不小于lowbit(x)。接着发现,当a取lowbit(x)时,由于x和a的二进制最右边的1的位置相同,因此x+a会在这个1的位置上产生进位,使得进位过程中的所有连续的1变成0,直到把它们左边第一个0置为1时结束。于是lowbit(x+a)>lowbit(x)显然成立,最小的a就是lowbit(x)。
于是update函数的做法就很明确了,只要让x不断加上lowbit(x),并让每步的C[x]都加上v,直到x超过给定的数据范围为止(因为在不给定数据范围的情况下,更新操作是无上
限的)。
void add(int x,int v)
{
for(int i=x;i<=n;i+=lowbit(i))
c[i]+=v;
}
显然,这个过程是从右至左不断定位x的二进制最右边的1左边的0的过程,因此update函数的时间复杂度为0(logN)。同样的,从另一个角度理解,update函数的过程实际上是在沿着一条不断右上的路径行进。于是由于“树”高是O(logN)级别,因此可以同样得到update函数的时间复杂度就是O(logN)。
看起来update 函数和getSum函数的代码相当简洁,事实上它们就是树状数组的最核心的“武器”,通过它们就能解决一系列问题, 接下来来看树状数组最经典的应用。
问题是这样的:给定一一个有N个正整数的序列A (\(N≤10, A[i]≤10^5\))。
先来看使用hash数组的做法,其中hash[x]记录整数x当前出现的次数。接着,从左到右遍历序列A,假设当前访问的是A[i],那么就令hash[A[i]]加1,表示当前整数A[j]的出现次数增加了一次;同时,序列中在A[i]左边比A[i]小的数的个数等于hash[1] + hassh[2] +...+hasb[A[i]- 1],这个和需要输出。但是很显然,这两个工作可以通过树状数组的update(A[i], 1)和getSum(A[i]- 1)来解决。
使用树状数组时,不必真的建一个hash 数组,因为它只存在于解法的逻辑中,并不需要真的用到,只需用一个树状数组来代替它即可。
这就是树状数组最经典的应用,即统计序列中在元素左边比该元素小的元素个数,其中“小”的定义根据题目而定,并不一定必须是数值的大小。
那么,如何统计序列中在元素左边比该元素大的元素个数呢?事实上这等价于计算hash[A[i]+ 1] +...+ hash[N],于是getSum(N) - getSum(A[i])就是答案。至于统计序列中在元素右边比该元素小(或大)的元素个数,只需要把原始数组从右往左遍历就好了。
但是现在还有问题没有解决:如果A[i]≤N 不成立(例如A[i]≤\(10^9\)),看起来树状数组开不了那么大,是不是就没办法了呢?当然不是。举个例子,现在给定一个序列A为{520,
99999999, 18, 666, 8888},如果只需要考虑它们之间大小的关系,那么这个序列实际上和{2,5,1,3,4}是等价的。同样的,序列{11, 111, 1, 11}与{2,4,1,2}也是等价的(当然只考虑大小关系的话与{2,3,1,2}等价也是可以的)。因此要做的就是把A[i]与1~N对应起来,而这与“给定N个学生的分数,给他们进行排名,分数相同则排名相同”显然是同一个问题。一般来说,可以设置一个临时的结构体数组,用以存放输入的序列元素的值以及原始序号,而在输入完毕后将数组按val从小到大进行排序,排序完再按照“计算排名”的方式将“排名”根据原始序号pos存入一个新的数组即可。由于这种做法可以把任何不在合适区间的整数或者非整数都转换为不超过元素个数大小的整数,因此一般把这种技巧称为离散化。下面针对“统计序列中在元素左边比该元素小的元素个数”的问题给出使用离散化的代码:
一般来说,离散化只适用于离线查询,因为必须知道所有出现的元素之后才能方便进行离散化。但是对在线查询来说也不是一点办法都没有,也可以先把所有操作都记录下来,然后对其中出现的数据进行离散化,之后再按照记录下来的操作顺序正常进行“在线”查询即可。


