《算法笔记》——第十章 拓扑排序&关键路径 学习记录
拓扑排序
如果一个有向图的任意顶点都无法通过一些有向边回到自身,那么称这个有向图为有向无环图(Directed Acyclic Graph, DAG)。
拓扑排序是将有向无环图G的所有顶点排成一个线性序列,使得对图G中的任意两个顶点u、v,如果存在边u->v,那么在序列中u一定在v前面。这个序列又被称为拓扑序列。
- 定义一个队列Q,并把所有入度为0的结点加入队列。
- 取队首结点,输出。然后删去所有从它出发的边,并令这些边到达的顶点的入度减1,
- 反复进行②操作,直到队列为空。如果队列为空时入过队的结点数目恰好为N,说明拓扑排序成功,图G为有向无环图;否则,拓扑排序失败,图G中有环。
拓扑排序的很重要的应用就是判断一个给定的图是否是有向无环图。
最后指出,如果要求有多个入度为0的顶点,选择编号最小的顶点,那么把queue改成priority_queue,并保持队首元素(堆顶元素)是优先队列中最小的元素即可(当然用set也是可以的)。
关键路径
顶点活动(Activity On Vertex,AOV)网是指用顶点表示活动,而用边集表示活动间优先关系的有向图。例如先导课程示意图就是AOV网,其中图的顶点表示各项课程,也就是“活动”;有向边表示课程的先导关系,也就是“活动间的优先关系”。显然,图中不应当存在有向环,否则会让优先关系出现逻辑错误。
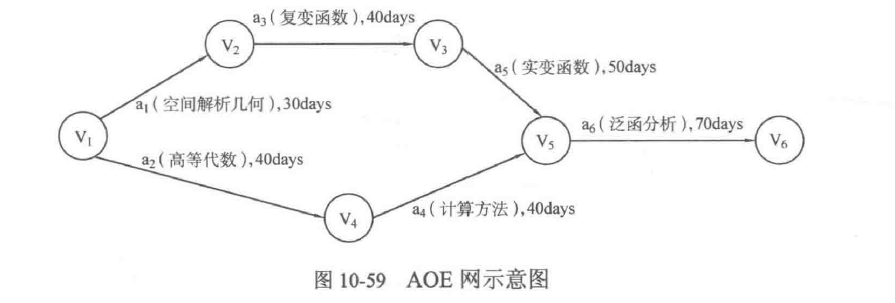
边活动(Activity On Edge,AOE) 网是指用带权的边集表示活动,而用顶点表示事件的有向图,其中边权表示完成活动需要的时间。例如图10-59中,边a1 ~ a6表示需要学习的课程,也就是“活动”,边权表示课程学习需要消耗的时间;顶点V1 ~ V6表示到此刻为止前面的课程已经学完,后面的课程可以开始学习,也就是“事件”(如V5表示a4计算方法和as实变函数已经学完,a6泛函分析可以开始学习。
从另一个角度来看,a6只有当a4和a5都完成时才能开始进行,因此当a4计算方法学习完毕后必须等待a5实变函数学习完成后才能进入到a6
泛函分析的学习),显然“事件”仅代表一个中介状态。
一般来说, AOE网用来表示一个工程的进行过程,而工程常常可以分为若千个子工程(即“活动”),显然AOE网不应当有环,否则会出现和AOV网一样的逻辑问题(因此可以认为AOV网和AOE网都是有向无环图)。
考虑到对工程来说总会有一个起始时刻和结束时刻,因此AOV网一般只有一个源点(即入度为0的点)和一个汇点(即出度为0的点)。
不过虽然这么说,实际上即便有多个源点和多个汇点,仍然可以转换为一个源点和一个汇点的情况,也就是添加一个“超级源点”和一个“超级汇点”的方法,即从超级源点出发,连接所有入度为0的点;从所有出度为0的点出发,连接超级汇点;添加的有向边的边权均为0。
需要指出,如果给定AOV网中各顶点活动所需要的时间,那么就可以将AOV网转换为AOE网。比较简单的方法是:将AOV网中每个顶点都拆成两个顶点,分别表示活动的起点和终点,而两个顶点之间用有向边连接,该有向边表示原顶点的活动,边权给定;原AOV网中的边全部视为空活动,边权为0。
既然AOE网是基于工程提出的概念,那么一定有其需要解决的问题。AOE网需要着重解决两个问题:
- 工程起始到终止至少需要多少时间;
- 哪条(些)路径上的活动是影响整个工程进度的关键。
AOE网中的最长路径被称为关键路径(强调:关键路径就是AOE网的最长路径),而把关键路径上的活动称为关键活动,显然关键活动会影响整个工程的进度。
有读者可能会问,既然关键路径的定义是AOE网中的最长路径,为什么其长度会等于整个工程的最短完成时间呢?如何理解此处的“最长”和“最短”?事实上这只是从两个角度看待而已。
从时间的角度上看,不能拖延的活动严格按照时间表所达到的就是最短时间;而从路径长度的角度上看,关键路径选择的总是最长的道路。仔细思考便会发现,所谓“不能拖延的活动”就是最长路径上的活动,因此最长路径长度和最短时间是相同的。
最长路径
对一个没有正环的图(指从源点可达的正环,下同),如果需要求最长路径长度,则可以把所有边的边权乘以-1,令其变为相反数,然后使用Bellman-Ford 算法或SPFA算法求最短路径长度,将所得结果取反即可。
注意:此处不能使用Dijkstra 算法,原因是Djkstra算法不能处理负边权的情况,即便原图的边权均为正,乘以-1之后也会出现负权。
显然,如果图中有正环,那么最长路径是不存在的。但是,如果需要求最长简单路径(也就是每个顶点最多只经过一次的路径),那么虽然最长简单路径本身存在,却没有办法通过Bellman-Ford等算法来求解,原因是最长路径问题是NP-Hard问题(也就是没有多项式时间复杂度算法的问题)。
注:最长路径问题,即Longest Path Problem,寻求的是图中的最长简单路径。
而如果求的是有向无环图的最长路径长度,则关键路径的求法可以比上面的做法更快。
关键路径
由于AOE网实际上是有向无环图,而关键路径是图中的最长路径,因此本节实际上给出了一种求解有向无环图(DAG)中最长路径的方法。
由于关键活动是那些不允许拖延的活动,因此这些活动的最早开始时间必须等于最迟开始时间。因此可以设置数组e和1,其中e[r]和[r]分别表示活动ar的最早开始时间和最迟开始时间。于是,当求出这两个数组之后,就可以通过判断e[r]==l[r]是否成立来确定活动r是否是关键活动。



