《算法笔记》第十章——最短路 学习记录
Dijkstra算法
Dijkstra算法(读者可以将其读作“迪杰斯特拉算法”)用来解决单源最短路问题,即给定图G和起点s,通过算法得到s到达其他每个顶点的最短距离。Dijkstra的基本思想是对图G(V,E)设置集合S存放已被访问的顶点,然后每次从集合V-S中选择与起点s的最短距离最小的一个顶点(记为u),访问并加入集合S。之后,令顶点u为中介点,优化起点s与所有从u能到达的顶点v之间的最短距离。这样的操作执行n次(n为顶点个数),直到集合S已包含所有顶点。
Dijkstra算法的策略是:
设置集合S存放已被访问的顶点(即已攻占的城市),然后执行n次下面的两个步骤(n为顶点个数):
- 每次从集合V-S中选择与起点s的最短距离最小的一个顶点(记为u),访问并加入集合S。
- 之后,令顶点u为中介点,优化起点s与所有从u能到达的顶点v之间的最短距离。
碰到这种有两条及以上可以达到最短距离的路径,题目就会给出一个第二标尺(第一标尺是距离),要求在所有最短路径中选择第二标尺最优的一条路径。而第二标尺常见的是以下三种出题方法或其组合:
- 给每条边再增加-一个边权(比如说花费),然后要求在最短路径有多条时要求路径上的花费之和最小(如果边权是其他含义,也可以是最大)。
- 给每个点增加一个点权(例如每个城市能收集到的物资),然后在最短路径有多条时要求路径上的点权之和最大(如果点权是其他含义的话也可以是最小)。
- 直接问有多少条最短路径。
细心的读者应当注意到,上面给出的3种情况都是以路径上边权或点权之"和”为第二标尺的,例如路径上的花费之和最小、路径上的点权之和最小、最短路径的条数都体现了“和”的要求。事实上也可能出现一些逻辑更为复杂的计算边权或点权的方式,此时按上面的方式只使用Djkstra算法就不一定能算出正确的结果(原因是不一定满足最优子结构),或者即便能算出,其逻辑也极其复杂,很容易写错。
这里介绍一种更通用、又模板化的解决此类问题的方式一Dijkstra + DFS。回顾上面只使用Djkstra算法的思路,会发现,算法中数组pre总是保持着最优路径,而这显然需要在执行Dijkstra算法的过程中使用严谨的思路来确定何时更新每个结点v的前驱结点pre[v],实在容易出错。事实上更简单的方法是:先在Djjkstra算法中记录下所有最短路径(只考虑距离),然后从这些最短路径中选出一条第二标尺最优的路径(因为在给定一条路径的情况下,针对这条路径的信息都可以通过边权和点权很容易计算出来!)。
- 使用Dijkstra算法记录所有最短路径。
由于此时要记录所有最短路径,因此每个结点就会存在多个前驱结点,这样原先pre数组只能记录一个前驱结点的方法将不再适用。为了适应多个前驱的情况,不妨把pre数组定义为vector类型“vectorpre[MAXV]”,这样对每个结点v来说,pre[v]就是一 个变长数组,
里面用来存放结点v的所有能产生最短路径的前驱结点。(注:对需要查询某个顶点u是否在顶点v的前驱中的题目,也可以把pre数组设置为set数组,此时使用pre[v].count(u)来查询会比较方便)。
于是通过上面vector类型的pre数组,就可以使用DES来获取所有最短路径。
这里先讲解如何获取这个pre数组。之前已经提到过,在本处Djkstra 算法部分,只需要考虑距离这一个因素, 因此不必考虑第二标尺的干扰,而专心于pre数组的求解。在之前的写法中,pre[i]被初始化为i,表示每个结点在初始状态下的前驱为自身,但是在此处,pre数组一开始不需要赋初值(原因马上就会提到)。
接下来就是考虑更新d[v]的过程中pre数组的变化。首先,如果d[u]+ G[u][v] <d[v],说明以u为中介点可以使d[v]更优,此时需要令v的前驱结点为u。并且即便原先pre[v]中已经存放了若干结点,此处也应当先清空,然后再添加u。显然,对顶点v来说,由于每次找到更优的前驱时都会清空pre[v],因此pre数组不需要初始化。
之后,如果d[u] + G[u][v] == d[v],说明以u为中介点可以找到一条相同距离的路径,因此v的前驱结点需要在原先的基础上添加上u结点(而不必先清空pre[v])。
遍历所有最短路径,找出一条使第二标尺最优的路径。读者应该还记得,在之前的写法中曾使用一个递归来找出最短路径。此处的做法与之类似,不同点在于,由于每个结点的前驱结点可能有多个,遍历的过程就会形成一棵递归树。
显然,当对这棵树进行遍历时,每次到达叶子结点,就会产生一条完整的最短路径(想想之前的写法是什么样的树?——其实就是一条链)。因此,每得到一条完整路径,就可以对这条路径计算其第二标尺的值( 例如把路径上的边权或是点权累加出来),令其与当前第二标尺的最优值进行比较。如果比当前最优值更优,则更新最优值,并用这条路径覆盖当前的最优路径。这样,当所有最短路径都遍历完毕后,就可以得到最优第二标尺与最优路径。
接下来就要考虑如何写DFS的递归函数。
首先,根据上面的分析,必须要有的是:
- 作为全局变量的第二标尺最优值optValue。
- 记录最优路径的数组path(使用vector来存储)。
- 临时记录DFS遍历到叶子结点时的路径tempPath(也使用vector存储)。
然后,考虑递归函数的两大构成:递归边界与递归式。对递归边界而言,如果当前访问的结点是叶子结点(也即路径的起点st),那么说明到达了递归边界,此时tempPath存放了一条路径。这时要做的就是对这条路径求出第二标尺的值value,并与optValue比较,如果更优,则更新optValue并把tempPath覆盖path。
对递归式而言,如果当前访问的结点是v,那么只需要遍历pre[v]中的所有结点并进行递归即可。
最后说明如何在递归过程中生成tempPath。其实很简单,只要在访问当前结点v时将v加到tempPath的最后面,然后遍历pre[v]进行递归, 等pre[v]的所有结点遍历完毕后再把tempPath最后面的v弹出。只是要注意的是,叶子结点(也即路径的起点st)没有办法通过上面的写法直接加入tempPath,因此需要在访问到叶子结点时临时加入。
需要注意的是,由于递归的原因,存放在tempPath中的路径结点是逆序的,因此访问结点需要倒着进行。当然,如果仅是对边权或点权进行求和,那么正序访问也是可以的。
最后指出,如果需要同时计算最短路径(指距离最短)的条数,那么既可以按之前的做法在Dijkstra代码中添加num数组来求解,也可以开一个全局变量来记录最短路径条数,当DFS到达叶子结点时令该全局变量加1即可。
而如果题目有第三标尺、第四标尺,也可以用同样的思路进行解决,读者可以在练习题中可以找到这样的题目进行尝试。另外,如果题目较为简洁且只有第二标尺,可能还是用之前讲解的一遍Djkstra算法的求解过程更好写且更快。
Bellman-Ford算法和SPFA算法
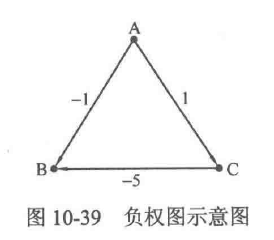
Dijkstra算法可以很好地解决无负权图的最短路径问题,但如果出现了负权边,Dijkstra算法就会失效,例如图10-39中设置A为源点时,首先会将点B和点C的dist值变为-1和1,接着由于点B的dist值最小,因此用点B去更新其未访问的邻接点(虽然并没有)。在这之后点B标记为已访问,于是将无法被从点C出发的边CB更新,因此最后dist[B]就是-1,但显然A到B的最短路径长度应当是A→C→B的-4。
为了更好地求解有负权边的最短路径问题,需要使用Bellman-Ford算法(简称BF算法)。和Djkstra算法一样,Bellman-Ford算法可解决单源最短路径问题,但也能处理有负权边的情况。Bellman-Ford 算法的思路简洁直接,易于读者掌握。
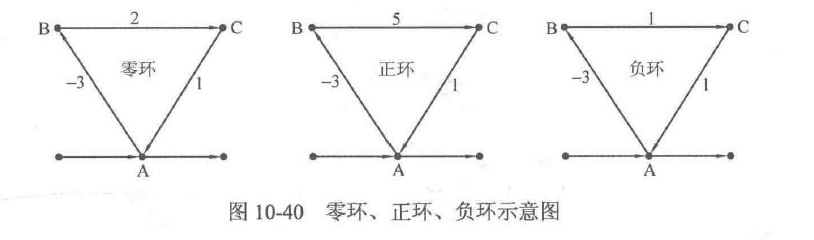
现在考虑环,也就是从某个顶点出发、经过若千个不同的顶点之后可以回到该顶点的情况。而根据环中边的边权之和的正负,可以将环分为零环、正环、负环(如图10-40所示,环A→B→C中的边权之和分别为0、正、负)。显然,图中的零环和正环不会影响最短路径的求解,因为零环和正环的存在不能使最短路径更短;而如果图中有负环,且从源点可以到达,那么就会影响最短路径的求解;但如果图中的负环无法从源点出发到达,则最短路径的求解不会受到影响。
与Dijkstra算法相同,Bellman-Ford算法设置一个数组d,用来存放从源点到达各个顶点的最短距离。同时Bellman-Ford算法返回一个bool值:如果其中存在从源点可达的负环,那么函数将返回false;否则,函数将返回true,此时数组d中存放的值就是从源点到达各顶点的最短距离。
Bellman-Ford算法的主要思路如下面的伪代码所示。需要对图中的边进行V- 1轮操作,每轮都遍历图中的所有边:对每条边u→v,如果以u为中介点可以使d[v]更小,即d[u]+length[u->v] < d[v]成立时,就用d[u] + length[u->v]更新d[v]。同时也可以看出,Bellman-Ford算法的时间复杂度是\(O(VE)\),其中n是顶点个数,E是边数。
for(int i=0;i<n-1;i++)
for(each edge u->v)
if(d[u] + length[u->v] < d[v])
d[v]=d[u]+length[u->v];
此时,如果图中没有从源点可达的负环,那么数组d中的所有值都应当已经达到最优。因此,如下面的伪代码所示,只需要再对所有边进行一轮操作,判断是否有某条边u→v仍然满足d[u] + length[u->v] < d[v],如果有,则说明图中有从源点可达的负环,返回false;否则,
说明数组d中的所有值都已经达到最优,返回true。
for(each edge u->v)
if(d[u] + length[u->v] < d[v])
return false;
return true;
那么,为什么BellmanFord算法是正确的呢?想要了解完整数学证明的读者可以参考算法导论,下面给出一个简洁直观的证明。
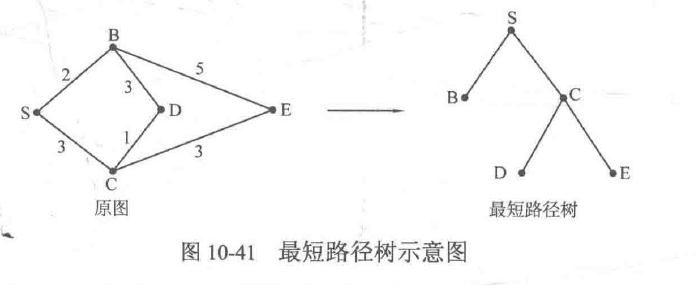
首先,如果最短路径存在,那么最短路径上的顶点个数肯定不会超过V个。于是,如果把源点s作为一棵树的根结点,把其他结点按照最短路径的结点顺序连接,就会生成一棵最短路径树。 图10-41 是最短路径树的一个例子。显然,在最短路径树中,从源点S到达其余各顶点的路径就是原图中对应的最短路径,且原图和源点一且确定,最短路径树也就确定了。另外,由于最短路径上的顶点个数不超过V个,因此最短路径树的层数一定不超过V。
由于初始状态下d[s]为0,因此在接下来的步骤中d[s]不会被改变(也就是说,最短路径树中第一层结点的d值被确定)。接着,通过Bellman-Ford算法的第一轮操作之后,最短路径树中的第二层顶点的d值也会被确定下来;然后进行第二轮操作,于是第三层顶点的d值也被确定下来。这样计算直到最后一层顶点的d值确定。由于最短路径树的层数不超过V层,因此Bellman-Ford算法的松弛操作不会超过V-1轮。证毕。
由于Bellman-Ford算法需要遍历所有边,显然使用邻接表会比较方便;如果使用邻接矩阵,则时间复杂度会上升到\(O(V3)\)。
注意到,如果在某一轮操作时,发现所有边都没有被松弛,那么说明数组d中的所有值都已经达到最优,不需要再继续,提前退出即可,这样做可以稍微加快一点速度。
至于最短路径的求解方法、有多重标尺时的做法均与Dijkstra算法中介绍的相同,此处不再重复介绍。唯一要注意的是统计最短路径条数的做法:由于Bellman-Ford算法期间会多次访问曾经访问过的顶点,如果单纯按照Djkstra算法中介绍的num数组的写法,将会反复累计已经计算过的顶点。
为了解决这个问题,需要设置记录前驱的数组set
虽然Bellman-Ford算法的思路很简洁,但是\(O(VE)\)的时间复杂度确实很高,在很多情况下并不尽如人意。仔细思考后会发现,Bellman-Ford 算法的每轮操作都需要操作所有边,显然这其中会有大量无意义的操作,严重影响了算法的性能。
于是注意到,只有当某个顶点u的d[u]值改变时,从它出发的边的邻接点v的d[v]值才有可能被改变。由此可以进行一个优化:建立一个队列,每次将队首顶点u取出,然后对从u出发的所有边u→v进行松弛操作,也就是判断d[u] + length[u->v] < d[v]是否成立,如果成立,则用d[u] + length[u->v]覆盖d[v],于是d[v]获得更优的值,此时如果v不在队列中,就把v加入队列。这样操作直到队列为空
(说明图中没有从源点可达的负环),或是某个顶点的入队次数超过V-1 (说明图中存在从源点可达的负环)。
这种优化后的算法被称为SPFA (Shortest Path Faster Algorithm),它的期望时间复杂度是\(O(kE)\),其中E是图的边数,k是一个常数,在很多情况下k不超过2,可见这个算法在大部分数据时异常高效,并且经常性地优于堆优化的Djkstra算法。
但如果图中有从源点可达的负环,传统SPFA的时间复杂度就会退化成\(O(VE)\)。
另外,如果事先知道图中不会有环,那么num数组的部分可以去掉。注意:使用SPFA可以判断是否存在从源点可达的负环,如果负环从源点不可达,则需要添加一个辅助顶点C,并添加一条从源点到达C的有向边以及V-1条从C到达除源点外各顶点的有向边才能判断负环是否存在。
SPFA十分灵活,其内部的写法可以根据具体场景的不同进行调整。例如上面代码中的FIFO队列可以替换成优先队列(priority queue),以加快速度;或者替换成双端队列(deque),使用SLF优化和LLL优化,以使效率提高至少50%。除此之外,上面给出的代码是SPFA的BFS版本,如果将队列替换成栈,则可以实现DFS版本的SPFA,对判环有奇效。
Floyd算法
Floyd算法(读者可以将其读作“弗洛伊德算法”)用来解决全源最短路问题,即对给定的图G(V,E),求任意两点u, v之间的最短路径长度,时间复杂度是\(O(n^3)\)。由于\(O(n^3)\)的复杂度决定了顶点数n的限制约在200以内,因此使用邻接矩阵来实现Floyd算法是非常合适且方
便的。
Floyd算法基于这样一个事实:如果存在顶点k,使得以k作为中介点时顶点i和顶点j的当前最短距离缩短,则使用顶点k作为顶点i和顶点j的中介点,即当dis[i][k] + dis[k][] < dis[i][j]时,令dis[i][j] = dis[i][k] + dis[k][j] (其中dis[i][j]表示从顶点i到
顶点j的最短距离)。
对Floyd算法来说,需要注意的是:不能将最外层的k循环放到内层(即产生i->j->k的三重循环),这会导致最后结果出错。理由是:如果当较后访问的dis[u][v]有了优化之后,前面访问的dis[i][j]会因为已经被访问而无法获得进一步优化(这里i、j先于u、v进行访问)。



