《算法笔记》——第九章 堆 学习记录
堆是一棵完全二叉树,树中每个结点的值都不小于(或不大于)其左右孩子结点的值。
其中,如果父亲结点的值大于或等于孩子结点的值,那么称这样的堆为大顶堆,这时每个结点的值都是以它为根结点的子树的最大值,如果父亲结点的值小于或等于孩子结点的值,那么称这样的堆为小顶堆,这时每个结点的值都是以它为根结点的子树的最小值。
堆一般用于优先队列的实现,而优先队列默认情况下使用的是大顶堆,因此本节以大顶堆为例,以下出现的堆均指大顶堆。
现在有一所魔法学校,学校为了促进竞争,把学生的实力排成了堆的完全二叉树的形状,并规定每一棵子树都组成一支小分队,这样每个人都处在某一棵子树的根结点,代表着这支小分队的最高实力水平;同时,学院还让每个人都担任以他为根结点的小分队的队长。例如从图9-43中可以发现,紫微同学的实力是最强的,他是整个学院的TOP队长;而七杀同学则比太阴、巨门、天机、武曲、天同的实力更强,是他们这个小分队的队长;另外,七杀同学跟破军同学之间没有实力的比较(至少只从堆的结构中没办法看出来),只知道他们是各自小分队中的最强者,且他们都比紫微同学要弱。
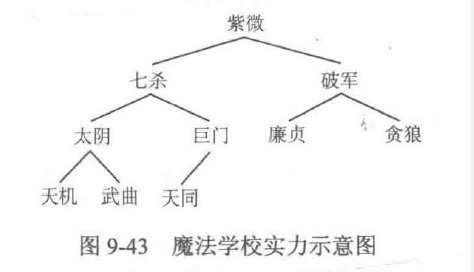
那么,对一个给定的初始序列,怎样把它建成一一个堆呢?以魔法学校为例,假设学生报到注册的顺序如下(括号内是他们的实力值):
廉贞(85)、武曲(55)、 贪狼(82)、天机(57)、 巨门(68)、 破军(92)、 紫微(99)、 七杀(98)、 太阴(66)、天同(56)。
将他们按照树的层序从上往下、从左往右依次摆放,就会形成图9-44所示的初始堆。
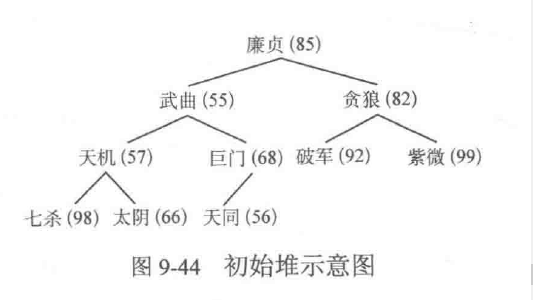
现在要调整这个初始堆,使得调整完成后能使每个位置都是各自小分队中实力最强的人,这样才算是一个真正的堆。依照首任校长传承至今的方法如下:
从最后一名同学的位置开始,从下往上,从右往左,从右往左。假设当前同学为X,那么学校让X与以X为队长的小分队的下一级的同学进行比试(例如武曲同学将与天机同学和巨门同学比试),如果发现当中有比他实力更强的同学,假设那其中实力最强的同学是Y,就交换X与Y的位置,这样Y同学就上升一级当队长,而X同学就只能当下一级的队长。交换之后让X继续与下一级的同学比试,直到他下一级的同学都比他弱或者他没有下一级的同学为止。
观察初始堆,会发现天同、太阴、七杀、紫微、破军都没有下一级,因此可以直接跳过。下面从巨门同学开始:
- 巨门同学。巨门同学(68)的下一级只有天同同学(56),但是天同同学比巨门同学弱,因此不需要做出调整。
- 天机同学。天机同学(57)的下一级有七杀同学(98)和太阴同学(66),由于七杀同学和太阳同学都比天机同学强,且七杀同学的实力是他们中最高的,因此交换七杀同学与天机同学的位置。之后天机同学不存在下一级,调整结束,调整后的情况如图9-45所示。
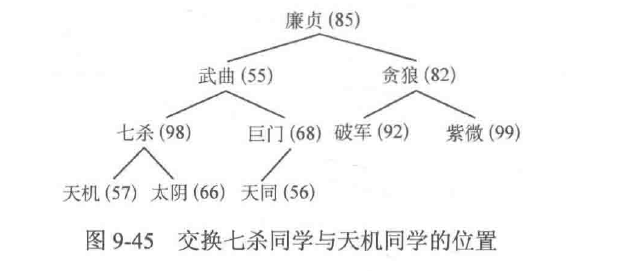
- 贪狼同学。贪狼同学(82)的下一级有破军同学(92)和紫微同学(99),由于破军同学和紫微同学都比天机同学强,且紫微同学的实力是他们中最高的,因此交换紫微同学与贪狼同学的位置。之后贪狼同学不存在下一级,调整结束,调整后的情况如图9-46所示。
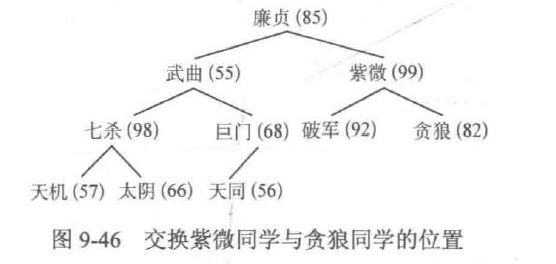
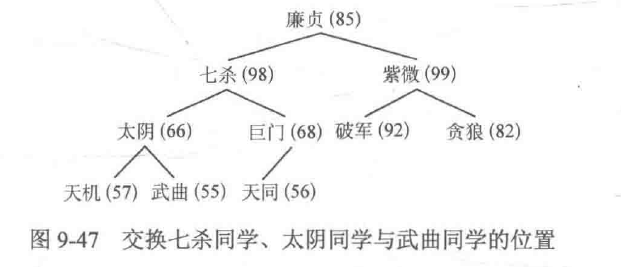
- 武曲同学。武曲同学(55)的下一级有七杀同学(98)和巨门同学(68),由于七杀同学和巨门同学都比武曲同学强,且七杀同学的实力是他们中最高的,因此交换七杀同学与武曲同学的位置。之后武曲同学下一级有天机同学(57)和太阴同学(66),由于天机同学和太阴同学都比武曲同学强,且太阴同学的实力是他们中最高的,因此交换太阴同学与武曲同学的位置。之后武曲同学不存在下一级,调整结束,调整后的情况如图9-47所示。
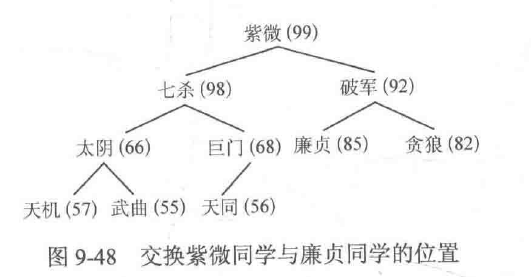
- 廉贞同学。廉贞同学(85)的下一级有七杀同学(98)和紫微同学(99),由于七杀同学和紫微同学都比廉贞同学强,且紫微同学的实力是他们中最高的,因此交换紫微同学与廉贞同学的位置。之后廉贞同学下一级有破军同学(92)和贪狼同学(82),由于破军同学比廉贞同学强,因此交换破军同学与廉贞同学的位置。之后廉贞同学不存在下一级,调整结束,调整后的情况如图9-48所示。
至此,建堆就完成了。那么具体怎么实现呢?对完全二叉树来说,比较简洁的实现方法是按照9.1.3节中介绍的那样,使用数组来存储完全二叉树。这样结点就按层序存储于数组中,其中第一个结点将存储于数组中的1号位,并且数组i号位表示的结点的左孩子就是2i号位,而右孩子则是(2i+1)号位。于是可以像下面这样定义数组来表示堆:
const int maxn=100;
int heap[maxn],n=10;
回顾之前的建堆过程会发现,每次调整都是把结点从上往下的调整。针对这种向下调整,调整方法是这样的:总是将当前结点V与它的左右孩子比较(如果有的话),假如孩子中存在权值比结点V的权值大的,就将其中权值最大的那个孩子结点与结点V交换;交换完毕后继续让结点V和孩子比较,直到结点V的孩子的权值都比结点V的权值小或是结点V不存在孩子结点。时间复杂度为\(O(logn)\)。
那么建堆的过程也就很容易了。假设序列中元素的个数为n,由于完全二叉树的叶子结点个数为\(\lceil{\frac{n}{2}}\rceil\)
,因此数组下标在\([1,\lfloor{\frac{n}{2}}\rfloor]\)范围内的结点都是非叶子结点。于是可以从\(\lfloor{\frac{n}{2}}\rfloor\)号位开始倒着枚举结点,对每个遍历到的结点i进行[i, n]范围的调整。为什么要倒着枚举呢?这是因为每次调整完一个结点后,当前子树中权值最大的结点就会处在根结点的位置,这样当遍历到其父亲结点时,就可以直接使用这个结果。也就是说,这种做法保证每个结点都是以其为根结点的子树中的权值最大的结点。
堆排序
堆排序是指使用堆结构对一个序列进行排序。此处讨论递增排序的情况。
考虑对一个堆来说,堆顶元素是最大的,因此在建堆完毕后,堆排序的直观思路就是取出堆顶元素,然后将堆的最后一个元素替换至堆顶,再进行一次针对堆顶元素的向下调整——如此重复,直到堆中只有一个元素为止。
具体实现时,为了节省空间,可以倒着遍历数组,假设当前访问到i号位,那么将堆顶元素与i号位的元素交换,接着在[1,i-1]范围内对堆顶元素进行一次向下调整即可。



