《算法笔记》——第九章 平衡二叉树 学习记录
首先来看看上一小节介绍的二叉查找树有什么缺陷。考虑使用序列{1,2,3,4,5}构建二叉查找树,会得到图9-24所示的二叉查找树。
显然这棵二叉查找树是链式的。
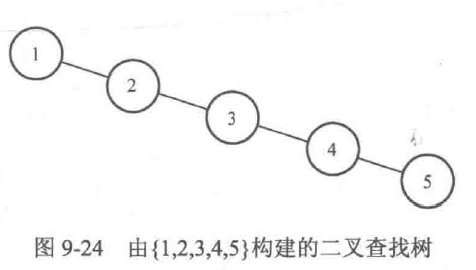
那么,一旦需要对有\(10^5\)级别个递增元素的序列构建二叉查找树,也将会得到一棵长长链条式的树,此时对这棵树中结点进行查找的复杂度就会达到\(O(n)\),起不到使用二叉查找树来进行数据查询优化的目的。
于是需要对树的结构进行调整,使树的高度在每次插入元素后仍然能保持\(O(logn)\)的级别,这样能让查询操作仍然是\(O(logn)\)的时间复杂度,于是就产生了平衡二叉树。
平衡二叉树由前苏联两位数学家GM.Adelse-Velskil和E.M.Landis提出,因此一般也称作AVL树。AVL树仍然是一棵二叉查找树,只是在其基础上增加了“平衡”的要求。所谓平衡是指,对AVL树的任意结点来说,其左子树与右子树的高度之差的绝对值不超过1,其中左子树与右子树的高度之差称为该结点的平衡因子。例如图9-25中的前两棵树就是AVL树,第3棵树不是AVL树,因为存在结点的平衡因子的绝对值大于1。
只要能随时保证每个结点平衡因子的绝对值不超过1,AVL的高度就始终能保持\(O(logn)\)级别。由于需要对每个结点都得到平衡因子,因此需要在树的结构中加入一个变量height,用来记录以当前结点为根结点的子树的高度:
struct Node
{
int v, height;
Node *lchild,*rchild;
};
在这种定义下,如果需要新建一个结点,就可以采用如下写法:
Node* newNode(int v)
{
Node* node = new Node;
node->v = v;
node->height = 1;
node->lchild = node->rchild = NULL;
return node;
}
显然,可以通过下面的函数获取结点root所在子树的当前高度:
int getHeight(Node* root)
{
if(root == NULL) return 0;
return root->height;
}
于是根据定义,可以通过下面的函数计算平衡因子:
int getBalanceFactor(Node* root)
{
return getHeight(root->lchild)-getHeight(root->rchild);
}
为什么不直接记录结点的平衡因子,而是记录高度?因为没有办法通过当前结点的子树的平衡因子计算得到该结点的平衡因子,而需要借助子树的高度间接求得。
显然,结点root所在子树的height等于其左子树的height与右子树的height的较大值加1,因此可以通过下面的函数来更新height:
void updateHeight(Node* root)
{
root->height=max(getHeight(root->lchild),getHeight(root->rchild))+1;
}
下面介绍AVL树的基本操作,为了讲解方便,以下假设每个结点的权值都不相同。
和二叉查找树相同,AVL树的基本操作有查找、插入、建树以及删除,由于删除操作较为复杂,因此主要介绍AVL树的查找、插入和建立。
查找操作
由于AVL树是一棵二叉查找树,因此其查找操作的做法与二叉查找树相同,具体可以参见二叉查找树的查找操作步骤。
由于AVL树的高度为\(O(logn)\)级别,因此AVL树的查找操作的时间复杂度为\(O(logn)\)。可以得到和二叉查找树的查找操作完全相同的代码:
void search(Node* root, int x)
{
if(root == NULL)
{
printf("search failed\n");
return;
}
if(x == root->data)
printf("%d\n",root->data);
else if(x < root->data)
search(root->lchild,x);
else
search(root->rchild,x);
}
插入操作
先抛开AVL树的插入问题,考虑图9-26左的二叉查找树,其中☆是结点A的左子树,◆和◇分别是结点B的左子树和右子树。本来大家相安无事,但是有一天结点B忽然觉得,既然A的权值比自己的权值小,凭什么必须让A当根结点呢?于是B找A商量,想自己来当根结点。A便同意了。但是由于基因的作用,它们将保证调整后的树仍然是一棵二叉查找树。
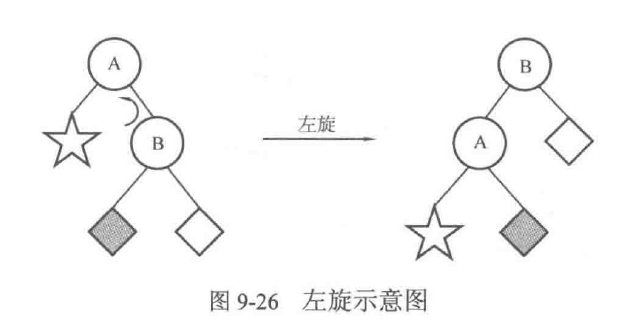
显然,☆上所有结点的权值都比结点A小,◇上所有结点的权值都比结点B大,因此不需要在调整中对☆和◇的位置进行改动(即☆仍然是结点A的左子树,◇仍然是结点B的右子树)。
那么◆的位置是否需要改动呢?当然是需要的,因为调整后B的左孩子将是结点A,因此◆必须移到其他地方去。移到哪里呢?考虑到A、B、◆的权值满足A<◆<B,于是让◆成为A的右子树即可。
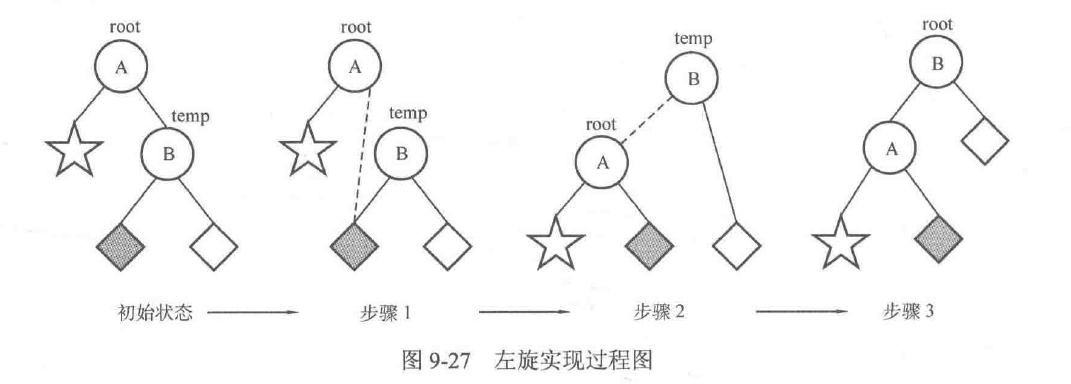
这个调整过程被称为左旋(Left Rotation)。假设指针root指向结点A,指针temp指向结点B,于是调整过程可以分为三个步骤,请结合图9-27理解。注意:图中黑色填充代表整个过程中该部分的父亲结点发生了变化,下同。调整步骤如下:
- 让B的左子树◆成为A的右子树。
- 让A成为B的左子树。
- 将根结点设定为结点B。
void L(Node* &root)
{
Node* temp = root->rchild;
root->rchild = temp->lchild;
temp->lchild = root;
updateHeight(root);
updateHeight(temp);
root=temp;
}
既然有左旋,一定会有右旋(Right Rotation)。事实上,右旋和左旋是对称的过程,于是可以把图9-26的右侧图进行右旋,将得到如图9-28所示的结果。
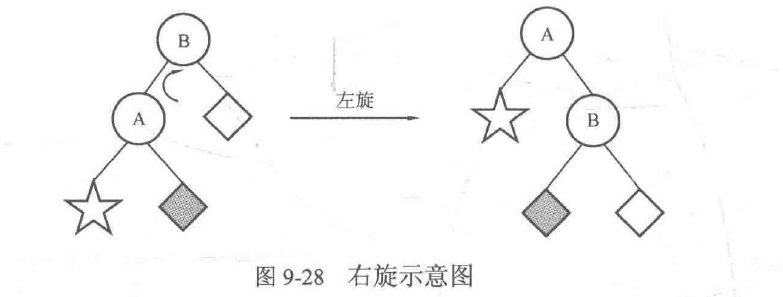
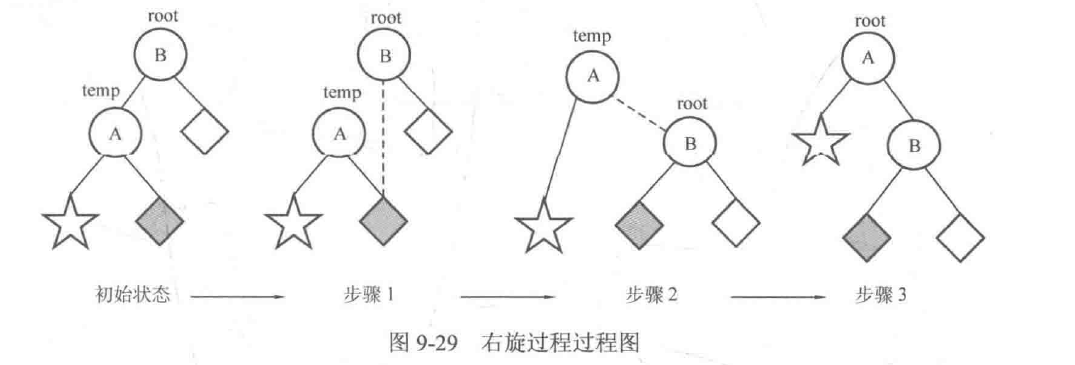
右旋的实现步骤和左旋基本相同,也是先移动◆,再改变AB的父子关系(可以结合图9-29理解):
- 让A的右子树◆成为B的左子树。
- 让B成为A的右子树。
- 将根结点设定为结点A。
void R(Node* &root)
{
Node* temp = root->lchild;
root->lchild = temp->rchild;
temp->rchild = root;
updateHeight(root);
updateHeight(temp);
root = temp;
}
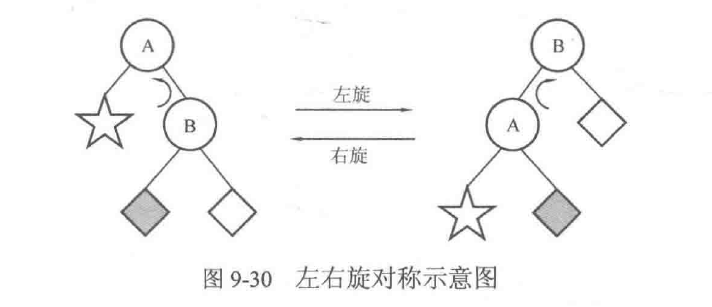
对比左旋和右旋的代码可以发现,两组代码只不过把代码中所有出现的left变成right、right变成left,由此也可以进一步理解左旋和右旋的对称本质一它们互为逆操作,如图9-30所示。
插入操作
关于旋转的讨论到此为止,接下来开始讨论AVL树的插入操作。
假设现在已有一棵平衡二叉树,那么可以预见到,在往其中插入一个结点时,一定会有结点的平衡因子发生变化,此时可能会有结点的平衡因子的绝对值大于1(这些平衡因子只可能是2或者-2),这样以该结点为根结点的子树就是失衡的,需要进行调整。
显然,只有在从根结点到该插入结点的路径上的结点才可能发生平衡因子变化,因此只需对这条路径上失衡的结点进行调整。可以证明,只要把最靠近插入结点的失衡结点调整到正常,路径上的所有结点就都会平衡。
假设最靠近插入结点的失衡结点是A,显然它的平衡因子只可能是2或者-2。很容易发现这两种情况完全对称,因此主要讨论结点A的平衡因子是2的情形。
由于结点A的平衡因子是2,因此左子树的高度比右子树大2,于是以结点A为根结点的子树一定是图9-31的两种形态LL型与LR型之一(注意: LL和LR只表示树型,不是左右旋的意思),其中☆、★、◇、◆是图中相应结点的AVL子树,结点A、B、C的权值满足
A>B>C。
可以发现,当结点A的左孩子的平衡因子是1时为LL型,是-1时为LR型。那么,为什么结点A的左孩子的平衡因子只可能是1或者-1,而不可能是0呢?这是因为这种情况无法由平衡二叉树插入一个结点得到。
补充说明,除了☆、★、◇、◆均为空树的情况以外,其他任何情况均满足在插入前底层两棵子树的高度比另外两棵子树的高度小1,且插入操作一定发生在底层两棵子树上。
例如对LL型来说,插入前子树的高度满足☆=★=◆-1=◇-1,而在☆或★中插入一个结点后导致☆或★的高度加1,使得结点A不平衡。
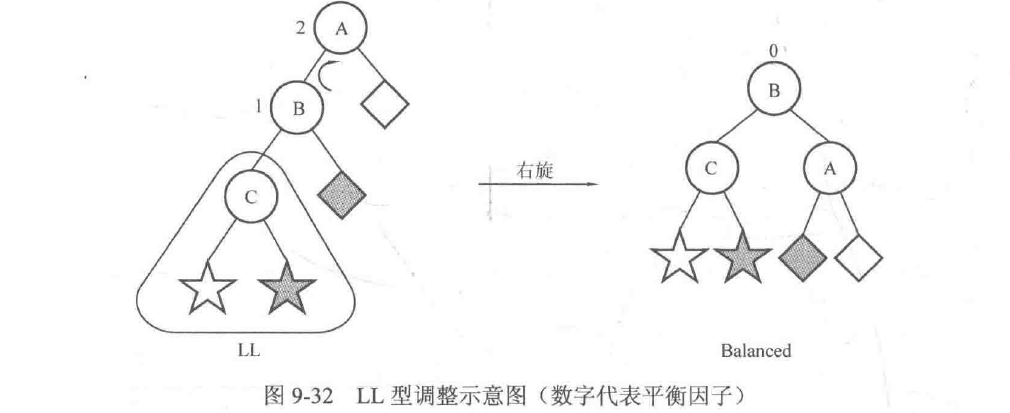
现在考虑怎样调整这两种树型,才能使树平衡。
先考虑LL型,可以把以C为根结点的子树看作一个整体,然后以结点A作为root进行右旋,便可以达到平衡,如图9-32所示。
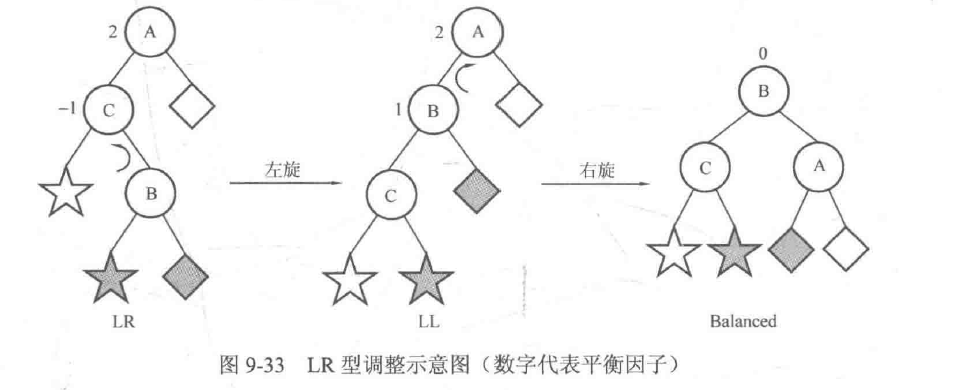
然后考虑LR型,可以先忽略结点A,以结点C为root进行左旋,就可以把情况转化为LL型,然后按上面LL型的做法进行一次右旋即可,如图9-33所示。
至此,结点A的平衡因子是2的情况已经讨论清楚,下面简要说明平衡因子是-2的情况,显然两种情况是完全对称的。
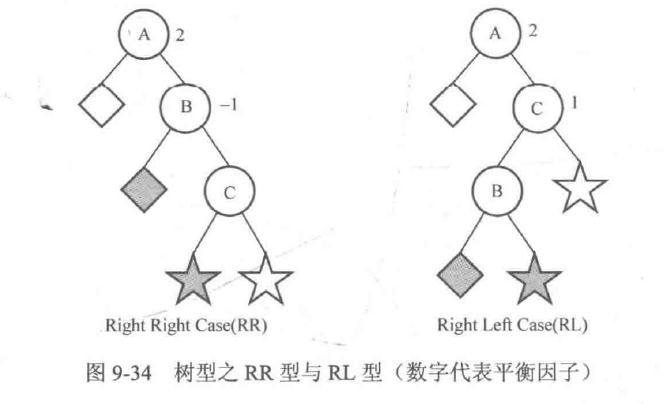
由于结点A的平衡因子为-2,因此右子树的高度比左子树大2,于是以结点A为根结点的子树一定是图9-34的两种形态RR型与RL型之一。
注意,由于和上面讨论的LL型和LR型对称,此处结点A、B、C的权值满足A<B<C。可以发现,当结点A的右孩子的平衡因子是-1时为RR型,是1时为RL型。
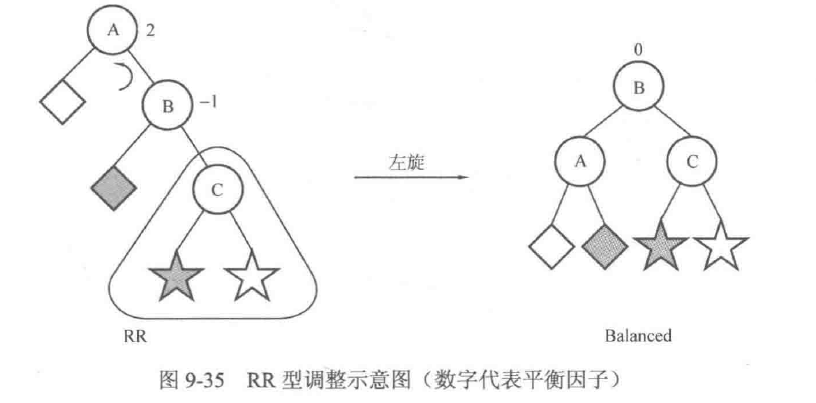
对RR型来说,可以把以C为根结点的子树看作一个整体,然后以结点A作为root进行左旋,便可以达到平衡,如图9-35所示。
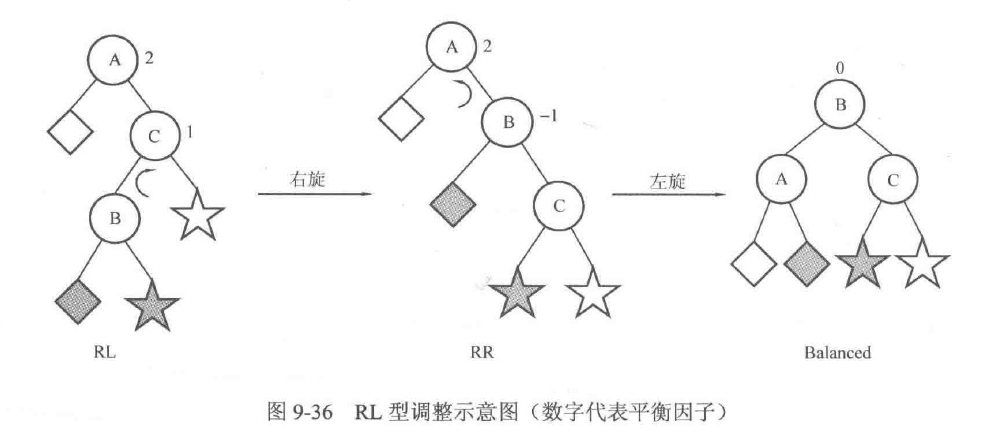
对RL型来说,可以先忽略结点A,以结点C为root进行右旋,就可以把情况转化为RR型,然后按上面RR型的做法进行一次左旋即可,如图9-36所示。
至此,对LL型、LR型、RR型、RL型的调整方法都已经讨论清楚,下面做个小小的汇总。

现在考虑如何书写插入代码。首先,AVL 树的插入代码是在二叉查找树的插入代码的基础上增加平衡操作的,因此,如果不考虑平衡操作,代码是下面这样的:
void insert(Node* root, int x)
{
if(root == NULL)
{
root = newNode(x);
return;
}
else if(x < root->data)
insert(root->lchild,x);
else
insert(root->rchild,x);
}
在这个基础上,由于需要从插入的结点开始从下往上判断结点是否失衡,因此需要在每个insert函数之后更新当前子树的高度,并在这之后根据树型是LL型、LR型、RR型、RL型之一来进行图9-33的平衡操作,代码如下:
void insert(Node* root, int x)
{
if(root == NULL)
{
root = newNode(x);
return;
}
if(x < root->data)
{
insert(root->lchild,x);
updateHeight(root);
if(getBalanceFactor(root) == 2)
{
if(getBalanceFactor(root->lchild) == 1) //LL
R(root);
else if(getBalanceFactor(root->lchild) == -1) //LR
{
L(root->lchild);
R(root);
}
}
}
else
{
insert(root->rchild,x);
updateHeight(root);
if(getBalanceFactor(root) == -2)
{
if(getBalanceFactor(root->rchild) == -1) //RR
L(root);
else if(getBalanceFactor(root->lchild) == 1) //RR
{
R(root->rchild);
L(root);
}
}
}
}
AVL树的建立
有了上面插入操作的基础,AVL树的建立就非常简单了,因为只需依次插入n个结点即可。代码如下:
Node* create(int data[], int n)
{
Node*root = NULL;
for(int i=0; i<n; i++)
insert(root,data[i]);
return root;
}



