《算法笔记》——第九章 二叉查找树 学习记录
二叉查找树(Binary Search Tree, BST)是一种特殊的二二叉树,又称为排序二叉树、二叉搜索树、二叉排序树。
二叉查找树的递归定义如下:
①要么二叉查找树是一棵空树。
②要么二叉查找树由根结点、左子树、右子树组成,其中左子树和右子树都是二叉查找树,且左子树上所有结点的数据域均小于根结点的数据域,右子树上所有结点的数据域均大于或等于根结点的数据域。
从二叉查找树的定义中可以知道,二叉查找树实际上是一棵数据域有序的二叉树,即对树_上的每个结点,都满足其左子树上所有结点的数据域均小于或等于根结点的数据域,右子树上所有结点的数据域均大于根结点的数据域。图9-18给出了几棵二叉查找树的示例。
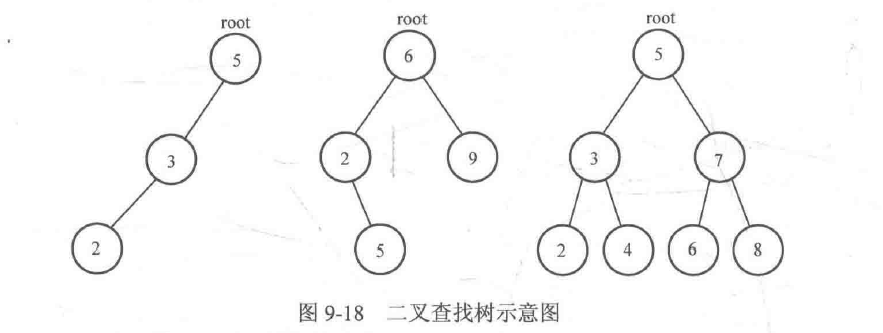
以图9-18的第三棵二叉查找树为例,根结点的数据域为5,其左子树结点的数据域均小于等于5,其右子树结点的数据域均大于5。而在以3为根的子树与以7为根的子树上,也满足上述条件(即2≤3<4, 6≤7<8)。
二叉查找树的基本操作有查找、插入、建树、删除。
查找操作
在之前介绍二叉树的查找操作时,由于无法确定二叉树的具体特性,因此只能对左右子树都进行递归遍历。但是二叉查找树的性质决定了读者可以只选择其中一棵子树进行遍历,因此查找将会是从树根到查找结点的一条路径,故最坏复杂度是\(O(h)\),其中h是二叉查找树的高度。
于是可以得到查找操作的基本思路:
- 如果当前根结点root为空,说明查找失败,返回。
- 如果需要查找的值x等于当前根结点的数据域root->data,说明查找成功,访问之。
- 如果需要查找的值x小于当前根结点的数据域root->data,说明应该往左子树查找,因此向root->lchild 递归。
- 如果需要查找的值x大于当前根结点的数据域root->data,说明应该往右子树查找,因此向root->rchild递归。
void search(Node* root, int x)
{
if(root == NULL)
{
printf("search failed\n");
return;
}
if(x == root->data)
printf("%d\n",root->data);
else if(x < root->data)
search(root->lchild,x);
else
search(root->rchild,x);
}
可以看到,和普通二叉树的查找函数不同,二叉查找树的查找在于对左右子树的选择递归。在普通二叉树中,无法确定需要查找的值x到底是在左子树还是右子树,但是在二叉查找树中就可以确定,因为二叉查找树中的数据域顺序总是左子树<根结点<右子树。
插入操作
对一棵二叉查找树来说,查找某个数据域的结点一定是沿着确定的路径进行的。因此,当对某个需要查找的值在二叉查找树中查找成功,说明结点已经存在;反之,如果这个需要查找的值在二叉查找树中查找失败,那么说明查找失败的地方一定是结点需要插入的地方。
因此可以在上面查找操作的基础上,在root=NULL时新建需要插入的结点。显然插入的时间复杂度也是\(O(h)\),其中h为二叉查找树的高度。
void insert(Node* root, int x)
{
if(root == NULL)
{
root = newNode(x);
return;
}
if(x == root->data)
return;
else if(x < root->data)
insert(root->lchild,x);
else
insert(root->rchild,x);
}
二叉查找树的建立
建立一棵二叉查找树,就是先后插入n个结点的过程,这和一般二叉树的建立是完全一样的,因此代码也基本相同:
Node* create(int data[], int n)
{
NOde* root = NULL;
for(int i=0;i<n;i++)
insert(root,data[i]);
return root;
}
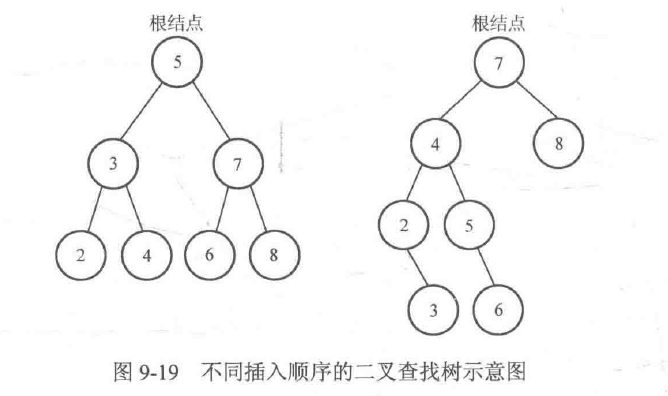
需要注意的是,即便是一组相同的数字,如果插入它们的顺序不同,最后生成的二叉查找树也可能不同。例如,先后插入{5,3, 7,4,2,8, 6}与{7, 4, 5, 8,2, 6, 3}之启可以得到两棵不
同的二叉查找树,如图9-19所示。
二叉查找树的删除
二叉查找树的删除操作一般有两种常见做法,复杂度都是\(O(h)\),其中h为二叉查找树的高度。此处主要介绍简单易写的一一种。
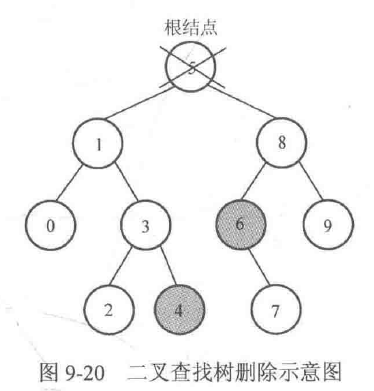
图9-20所示是一棵二叉查找树,如果需要删掉根结点5,应该怎么做呢?为了保证删除操作之后仍然是一棵二叉查找树,一种办法是以树中比5小的最大结点(也就是结点4)覆盖结点5,然后删除原
来的结点4;另一种办法是把树中比5大的最小结点(也就是结点6)覆盖结点5,然后删除原来的结点6。这两种做法都能保证删除操作之后仍然是一棵二叉查找树。
把以二叉查找树中比结点权值小的最大结点称为该结点的前驱,而把比结点权值大的最小结点称为该结点的后继。显然,结点的前驱是该结点左子树中的最右结点(也就是从左子树根结点开始不断沿着rchild 往下直到rchild为NULL时的结点),而结点的后继则是该结点右子树中的最左结点(也就是从右子树根结点开始不断沿着lchild往下直到lchild为NULL时的结点)。下面两个函数用来寻找以root为根的树中最大或最小权值的结点,用以辅助寻找结
点的前驱和后继:
Node* findMax(Node* root)
{
while(root->rchild != NULL)
root=root->rchild;
return root;
}
Node* findMin(Node* root)
{
while(root->lchild != NULL)
root=root->lchild;
return root;
}
假设决定用结点N的前驱P来替换N,于是就把问题转换为在N的左子树中删除结点P,就可以递归下去了,直到递归到一个叶子结点,就可以直接把它删除了。
因此删除操作的基本思路如下:
- 如果当前结点root为空,说明不存在权值为给定权值x的结点,直接返回。
- 如果当前结点root的权值恰为给定的权值x,说明找到了想要删除的结点,此时进入删除处理。
a)如果当前结点root不存在左右孩子,说明是叶子结点,直接删除。
b)如果当前结点root存在左孩子,那么在左子树中寻找结点前驱pre,然后让pre的数据覆盖root,接着在左子树中删除结点pre。
c)如果当前结点root存在右孩子,那么在右子树中寻找结点后继next,然后让next的数据覆盖root,接着在右子树中删除结点next。 - 如果当前结点root的权值大于给定的权值x,则在左子树中递归删除权值为x的结点。
- 如果当前结点root的权值大于给定的权值x,则在右子树中递归删除权值为x的结点。删除操作的代码如下(如果需要,可以在删除叶子结点的同时释放它的空间):
void deleteNode(Node* &root, int x)
{
if(root == NULL) return;
if(root->data == x)
{
if(root->lchild == NULL && root->rchild == NULL)
root=NULL;
else if(root->lchild != NULL)
{
Node* pre = findMax(root->lchild);
root->data = pre->data;
deleteNode(root->lchild,pre->data);
}
else
{
Node* next = findMin(root->rchild);
root->data = next->data;
deleteNode(root->rchild,next->data);
}
}
else if(root->data > x)
deleteNode(root->lchild,x);
else
deleteNode(root->rchild,x);
}
当然这段代码可以通过很多手段优化,例如可以在找到欲删除结点root的后继结点next后,不进行递归,而通过这样的手段直接删除该后继:假设结点next的父亲结点是结点S,显然结点next是S的左孩子,那么由于结点next一定没有左子树,便可以直接把结点next的右子树代替结点next成为S的左子树,这样就删去了结点next。前驱同理。
例如图9-20中结点5的后继是结点6,它是父亲结点8的左孩子,那么在用结点6覆盖结点5之后,可以直接把结点6的右子树代替结点6称为结点8的左子树。
为了方便操作,这个优化需要在结点定义中额外记录每个结点的父亲结点地址,有兴趣的读者可以自己尝试实现。
但是也要注意,总是优先删除前驱(或者后继)容易导致树的左右子树高度极度不平衡,使得二叉查找树退化成一条链。解决这一问题的办法有两种:一种是每次交替删除前驱或后继;另一种是记录子树高度,总是优先在高度较高的一棵子树里删除结点。
二叉查找树的性质
二叉查找树一个实用的性质:对二叉查找树进行中序遍历,遍历的结果是有序的。
这是由于二叉查找树本身的定义中就包含了左子树<根结点<右子树的特点,而中序遍历的访问顺序也是左子树→根结点→右子树,因此,所得到的中序遍历序列是有序的。
另外,如果合理调整二叉查找树的形态,使得树上的每个结点都尽量有两个子结点,这样整个二叉查找树的高度就会很低,也即树的高度大概在\(log(N)\)的级别,其中N是结点个数。能实现这个要求的一种树是平衡二叉树(AVL)。



