《算法笔记》——第五章 组合数 学习记录

关于n!的一个问题

n!表示n的阶乘，并且有n!=1x2x...xn成立。我们讨论一下关于它的一个问题: 求n!中有多少个质因子p。

这个问题是什么意思呢?举个例子，6!=1x2x3x4x5x6，于是6!中有4个质因子2，因为2、4、6中各有1个2、2个2、1个2；而6!中有两个质因子3，因为3、6中均各有1个3。

对这个问题，直观的想法是计算从1 ~ n的每个数各有多少个质因子p，然后将结果累加，时间复杂度为0(nlogn)，如下面的代码所示:

//计算n!中有多少个质因子p
int cal(int n,int p)
{
    int ans=0;
    for(int i=2;i<=n;i++)
    {
        int temp=i;
        while(temp % i == 0)
        {
            ans++;
            temp/=p;
        }
    }
    return ans;
}

但是这种做法对n很大的情况(例如n是\(10^{18}\))是无法承受的，我们需要寻求速度更快的方法。现在考虑10!中质因子2的个数，如图5-2所示。显然10!中有因子\(2^1\)的数的个数为5，有因子\(2^2\)的数的个数为2，有因子\(2^3\)的数的个数为1，因此10!中质因子2的个数为5+2+1=8。

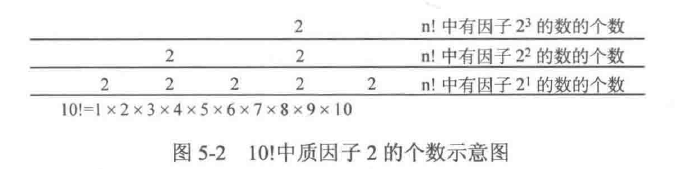
仔细思考便可以发现此过程可以推广为：n!中有\((\frac{n}{p}+\frac{n}{p^2}+\frac{n}{p^3}+\cdots)\)个质因子\(p\)，其中除法均为向下取整。于是便得到了\(O(logn)\)的算法，代码如下：

//计算n!中有多少个质因子p
int cal(int n,int p)
{
    int ans=0;
    while(n)
    {
        ans+=n/p;
        n/=p;
    }
    return ans;
}

利用这个算法，可以很快计算出n!的末尾有多少个零：由于末尾0的个数等于n!中因子10的个数，而这又等于n!中质因子5的个数(想一想为什么不是质因子2的个数？)，因此
只需要代入cal(n, 5)就可以得到结果。

这种算法还可以从另一种角度理解。还是以10!中质因子2的个数为例，将10!进行如下展开推导。

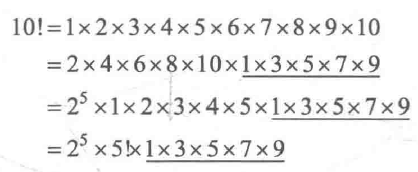
在上式的第二个等号处，把2的倍数放在左边、把非2的倍数放在右边；而在第三个等号处，将所有2的倍数都提出一个因子2(由于有10/2=5个2的倍数，因此提出25)，于是剩余的部分就变成了5!。显然，10!中质因子2的个数等于1 ~ 10中是2的倍数的数的个数5加上5!中质因子2的个数。可以对5!进行展开推导:

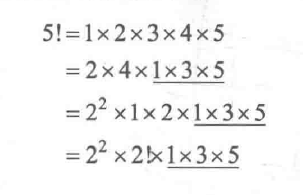
由上式可知5!中质因子2的个数等于1 ~ 5中是2的倍数的数的个数2 (由5/2=2得到)加上2!中质因子2的个数。同理可推得2!中质因子2的个数等于1，因此10!中质因子2的个数等于5+2+1=8。读者可以结合上面的代码进行理解。

将这个例子推广到一般情况可知，n!中质因子p的个数，实际上等于1 ~ n中p的倍数的个数\(\frac{n}{p}\)加上\(\frac{n}{p}!\)中质因子p的个数，这和之前的代码是吻合的。但是从这个结论中又可以看到递归的影子，因此也可以写出如下的递归版本，读者可以任选其一使用：

//计算n!中有多少个质因子p
int cal(int n,int p)
{
    if(n<p) return 0;
    return n/p+cal(n/p,p);
}

组合数的计算

组合数\(C_n^m\)是指从\(n\)个不同元素中选出\(m\)个元素的方案数\((m \le n)\)，一般也可以写成\(C(n,m)\)，其定义式为\(C_n^m=\frac{n!}{m!(n-m)!}\)，由三个整数的阶乘得到。通过定义可以知道，组合数满足\(C_n^m=C_n^{n-m}\)，且有\(C_n^0=C_n^n=1\)成立。本节讨论如下两个问题：

1. 如何计算\(C_n^m\)
2. 如何计算\(C_n^m\)%p

先来讨论第一个问题：如何计算\(C_n^m\)。此处给出\(3\)种方法。

方法一：通过定义式直接计算

首先从定义式入手来计算\(C_n^m\)。显然，由\(C_n^m=\frac{n!}{m!(n-m)!}\)，只需要先计算\(n!\)， 然后令其分别除以\(m!\)和\((n-m)!\)即可。但是显而易见的是，由于阶乘相当庞大，因此通过这种方式计算组合数能接受的数据范围会很小，即便使用long long类型来存储也只能承受\(n \le 20\)的数据范围。使用这种方法计算\(C_n^m\)的代码如下：

LL C(int n,int m)
{
    LL ans=1;
    for(int i=1;i<=n;i++) ans*=i;

    for(int i=1;i<=m;i++) ans/=i;

    for(int i=1;i<=n-m;i++) ans/=i;
    
    return ans;
}

这种明明\(C_n^m\)不大但却因为计算容易溢出的原因而无法得到正确值的做法显然是不太合适的，例如\(C(21, 10) = 352716\)，由上面的做法却因为\(21!\)超过long long型的数据范围而没办法算出来。这时需要从另外的角度来解决这个问题。

方法二：通过递推公式计算

下面介绍递推公式的方法。由于\(C_n^m\)表示从\(n\)个不同的数中选\(m\)个数的方案数，因此这可以转换为下面两种选法的方案数之和：

1. 一是不选最后一个数，从前\(n-1\)个数中选\(m\)个数；
2. 二是选最后一个数，从前\(n-1\)个数中选\(m-1\)个数。于是就可以得到下面这个递推公式：

\[C_n^m=C_{n-1}^m+C_{n-1}^{m-1} \]

从直观上看，公式总是把\(n\)减一，而把\(m\)保持原样或是减一， 这样这个递推式最终总可以把\(n\)和\(m\)变成相同或是让\(m\)变为0。而由定义可知\(C_n^0=C_n^n=1\)，这正好可以作为递归边界。于是很快会得到下面这个简洁的递归代码：

LL C(int n,int m)
{
    if(m == 0 || m == n) return 1;
    return C(n-1,m) + C(n-1,m-1);
}

在这种计算方法下完全不涉及阶乘运算，但是会产生另一个问题:重复计算。正如4.3.2节中介绍的斐波那契数列的例子，此处也会有很多\(C(n, m)\)是曾经已经计算过的，不应该重复计算。因此不妨记录下已经计算过的\(C(n, m)\)，这样当下次再次碰到时就可以作为结果直接返回了。如下面的递归代码:

LL res[67][67];

LL C(int n,int m)
{
    if(m == 0 || m == n) return 1;
    if(res[n][m]) return res[n][m];
    return res[n][m]=C(n-1,m) + C(n-1,m-1);
}

或者是下面这种把整张表都计算出来的递推代码：

const int n=60;

void cal()
{
    for(int i=0;i<=n;i++)
        for(int j=0;j<=i;j++)
            if(!j) res[i][j]=1;
            else res[i][j]=res[i-1][j]+res[i-1][j-1];
}

稍加画图可以发现，使用递归计算\(C(n, m)\)的时间复杂度和具体的数据有关，但单次计算\(C(n, m)\)不会超过\(O(n^2)\)，而递推计算所有\(C(n, m)\)的时间复杂度显然是\(O(n^2)\)，因此读者应当根据实际需要来选择使用递归还是递推。而觉得记不住这个公式的读者可以用具体例子\(10=C_5^2=C_4^2+C_4^1=6+4\)来记忆。

方法三：通过定义式的变形来计算

由于组合数的定义式为\(C_n^m=\frac{n!}{m!(n-m)!}\)，而这可以进行如下化简：

\[C_n^m=\frac{n!}{m!(n-m)!}=\frac{(n-m+1)\times(n-m+2)\times\cdots\times(n-m+m)}{1\times2\times\cdots\times m} \]

通过观察上式可以发现，分子和分母的项数恰好均为m项，因此不妨按如下方式计算：

\[C_n^m=\frac{(n-m+1)\times(n-m+2)\times\cdots\times(n-m+m)}{1\times2\times\cdots\times m}\\ =\frac{\frac{\frac{\frac{(n-m+1)}{1}\times(n-m+2)}{2}\times\cdots}{\cdots}\times(n-m+m)}{m} \]

这样，只要能保证每次除法都是整除，就能用这种“边乘边除”的方法避免连续乘法的溢出问题。那么，怎样证明每次除法都是整除呢?事实上这等价于证明\(\frac{(n-m+1)\times(n-m+2)\times\cdots\times(n-m+i)}{1\times2\times\cdots\times i}(1 \le i \le m)\)是个整数，不过这个结论是显然的，因为该式其实就是把\(C_{n-m+i}^{i}\)的定义式展开的结果，而\(C_{n-m+i}^{i}\)显然是个整数。

由此可以写出相应的代码，显然时间复杂度是\(O(m)\)。

LL C(int n,int m)
{
    LL ans=1;
    for(int i=1;i<=m;i++) 
        ans=ans*(n-m+i)/i;
    return ans;
}

不过这个程序有可能在最后一个乘法时溢出，因此实际上比方法二支持的数据范围小一点，然而差别不大。例如方法二在\(n=67、m=33\)时开始溢出，而方法三是在\(n=62、m=31\)时开始溢出。不过不管怎样，优秀的时间复杂度让它可以代替方法一。

至此已经介绍了三种计算组合数\(C_n^m\)的方法，但是一旦\(C_n^m\)本身超过了long long型，那么讨论就会失去意义。在这种情况下，可以使用5.6小节中的大整数运算来解决这个问题，但是这不是讨论的关键。一般来说，常见的情况是让运算结果对一个正整数p取模，也就是求\(C_n^m\%p\)，这才是所要讨论的内容。

接下来讨论第二个问题:如何计算\(C_n^m\%p\)，此处给出四种方法，它们有各自适合的数据范围，需要依照具体情况选择使用，但是一般来说方法一已经能满足需要。

方法一：通过递推公式计算

这种方法基于第一个问题的方法二，也是最容易、最实用的一种。只需要在原先的代码中适当的地方对p取模即可。为了说明问题方便，此处假设两倍的p不会超过int型。在这种做法下，算法可以很好地支持\(m \le n \le 1000\)的情况，并且对p的大小和素性没有额外限制(例如\(p \le 10\)都是可以的)。代码如下：

int res[1010][1010];

int C(int n,int m,int p)
{
    for(int i=0;i<=n;i++)
        for(int j=0;j<=i;j++)
            if(!j) res[i][j]=1;
            else res[i][j]=(res[i-1][j]+res[i-1][j-1])%p;
}

方法二：根据定义式计算

这种方法其实思路也很简单，基本过程是将组合数\(C_n^m\)进行质因子分解，假设分解结果为\(C_n^m=p_1^{c_1}\times p_2^{c_2} \times \cdots \times p_k^{c_k}\)，那么\(C_n^m\%p\)就等于\(p_1^{c_1}\times p_2^{c_2} \times \cdots \times p_k^{c_k}\%p\)，于是可以使用快速幂来计算每一组\(p_1^{c_1}\%p\)，然后相乘取模就能得到最后的结果。

那么怎样将\(C_n^m\)进行质因子分解呢？考虑到\(C_n^m=\frac{n!}{m!(n-m)!}\)，只需要遍历不超过\(n\)的所有质数\(p_i\)，然后计算\(n!、m!、(n- m)!\)中分别含质因子\(p_i\)的个数\(x、y、z\)(用5.8.1的方法)，于是就可以知道\(C_n^m\)中含质因子\(p_i\)的个数为\(x-y-z\)。由于\(C_n^m\)是个整数,因此\(x-y-z\)一定非负。

这种做法的时间复杂度为\(O(klogn)\)，其中\(k\)为不超过\(n\)的质数个数。由此可知能够支持\(m \le n \le 10^6\)的数据范围，并且对\(p\)的大小和素性没有额外限制。