《算法笔记》——第五章 gcd与lcm 学习记录
最大公约数
正整数a与b的最大公约数是指a与b的所有公约数中最大的那个公约数，例如4和6的最大公约数为2，3和9的最大公约数为3。一般用gcd(a, b)来表示a和b的最大公约数，而求解最大公约数常用欧几里得算法(即辗转相除法)。
欧几里得算法基于下面这个定理：
设a、b均为正整数，则gcd(a, b) = ged(b, a % b)。
证明：
设\(a=bk+c\)，显然有\(c=a \mod b\)。设\(d \mid a\)，\(d \mid b\)，则\(c=a-bk\)，\(\frac{c}{d}=\frac{a}{d}-\frac{b}{d}k\)。
由右边的式子可知\(c/d\)为整数，即\(d \mid c\)，所以对于\(a,b\)的公约数，它也会是\(a \mod b\)的一个约数，因此\(d\)是\(b\)和\(a \mod b\)的一个公约数。
反过来也需要证明：
设\(d \mid b\)，\(d \mid (a \mod b)\)，我们还是可以像之前一样得到以下式子：
因为左边式子显然为整数，所以\(\frac{a}{d}\)也为整数，即\(d \mid a\)，所以\(b,a \mod b\)的公约数也是\(a,b\)的公约数。
既然两式公约数都是相同的，那么最大公约数也会相同。
所以到式子\(gcd(a,b) = gcd(b,a \mod b)\)
由上面这个定理可以发现，如果a<b，那么定理的结果就是将a和b交换；如果a>b，那么通过这个定理总可以将数据规模变小，并且减小得非常快。这样似乎可以很快得到结果，只是还需要一个东西：递归边界，即数据规模减小到什么程度使得可以算出结果来。
很简单，众所周知: 0和任意一个整数a的最大公约数都是a(\(a \mid 0, a \mid a\))，这个结论就可以当作递归边界。由此很容易想到将其写成递归的形式，因为递归的两个关键已经得到。
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
最小公倍数
正整数a与b的最小公倍数是指a与b的所有公倍数中最小的那个公倍数，例如4和6的最小公倍数为12，3和9的最小公倍数为9。一般用lcm(a,b)来表示a和b的最小公倍数。
最小公倍数的求解在最大公约数的基础上进行。当得到a和b的最大公约数d之后，可以马上得到a和b的最小公倍数是ab/d。这个公式通过集合可以很好地理解,如图5-1所示。
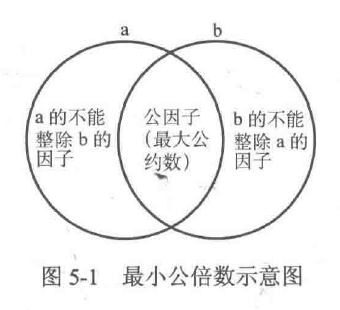
由图5-1很容易发现，a和b的最大公约数即集合a与集合b的交集，而最小公倍数为集合a与集合b的并集。要得到并集，由于ab会使公因子部分多计算一次，因此需要除掉一次公因子, 于是就得到了a与b的最小公倍数为ab/d。
由于ab在实际计算时有可能溢出，因此更恰当的写法是a/db。由于d是a和b的最大公约数，因此a/d一定可以整除。
int lcm(int a,int b)
{
return a/gcd(a,b)*b;
}
