贝叶斯模型、SVM模型、K均值模型、DBSCAN聚类

贝叶斯模型

通过已知类别的训练数据集，计算样本的先验概率

然后利用贝叶斯概率公式测算未知类别属于某个类别的后验概率

最终以最大后验概率所对应的类别作为样本的预测值

 

高斯贝叶斯分类器

适用于自变量为连续的数值类型的情况

 

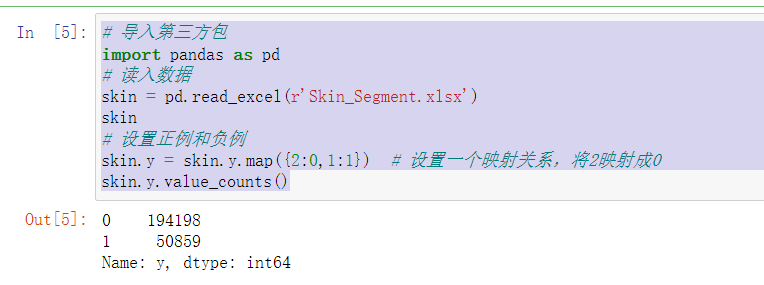
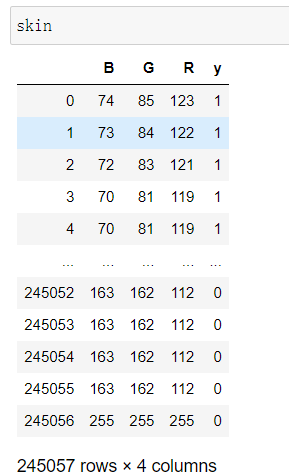
# 导入第三方包
import pandas as pd
# 读入数据
skin = pd.read_excel(r'Skin_Segment.xlsx')
skin
# 设置正例和负例
skin.y = skin.y.map({2:0,1:1})  # 设置一个映射关系，将2映射成0
skin.y.value_counts()

 

 

 

 

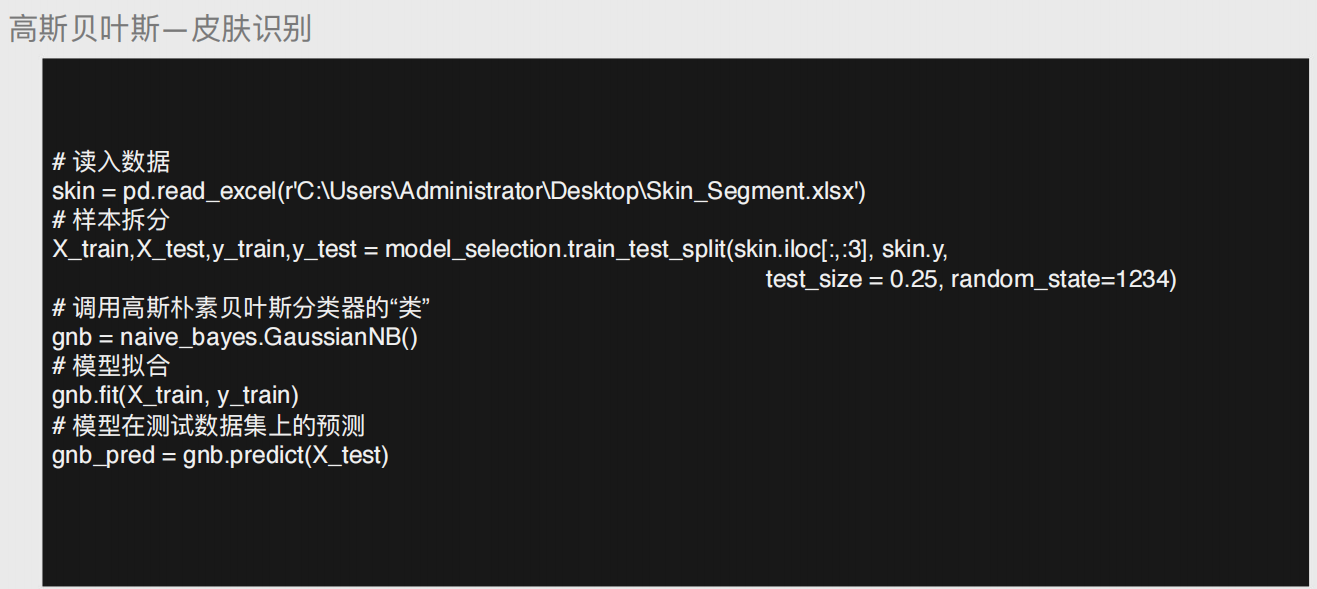
# 导入第三方模块
from sklearn import model_selection
# 样本拆分
X_train,X_test,y_train,y_test = model_selection.train_test_split(skin.iloc[:,:3], skin.y, 
                                                                 test_size = 0.25, random_state=1234)

# 导入第三方模块
from sklearn import naive_bayes
# 调用高斯朴素贝叶斯分类器的“类”
gnb = naive_bayes.GaussianNB()
# 模型拟合
gnb.fit(X_train, y_train)
# 模型在测试数据集上的预测
gnb_pred = gnb.predict(X_test)
# 各类别的预测数量
pd.Series(gnb_pred).value_counts()

 

 

 

 

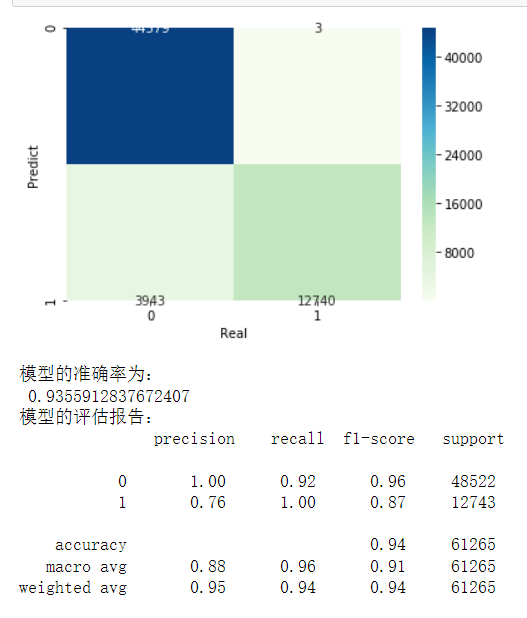
# 导入第三方包
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns
# 构建混淆矩阵
cm = pd.crosstab(gnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()

print('模型的准确率为：\n',metrics.accuracy_score(y_test, gnb_pred))
print('模型的评估报告：\n',metrics.classification_report(y_test, gnb_pred))

 

 

 

 

多项式贝叶斯分类器

适用于自变量为离散型类型的情况（非数字类型）

 

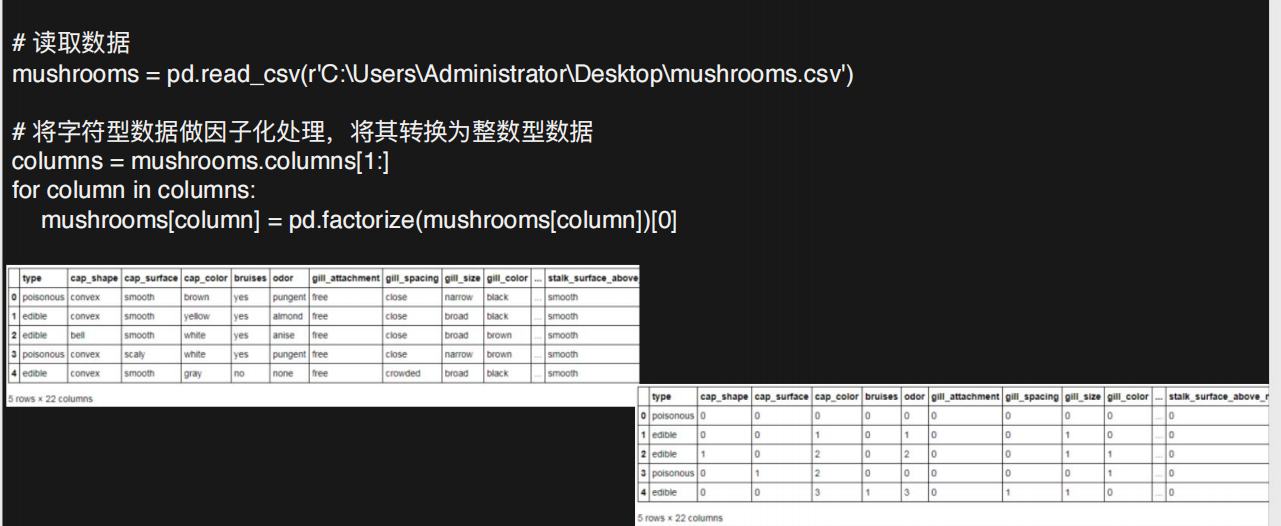
# 导入第三方包
import pandas as pd
# 读取数据
mushrooms = pd.read_csv(r'mushrooms.csv')
# 数据的前5行
mushrooms.head()

##################################################################
# 将字符型数据作因子化处理，将其转换为整数型数据
columns = mushrooms.columns[1:]
for column in columns:
    mushrooms[column] = pd.factorize(mushrooms[column])[0]
mushrooms.head()
##################################################################

 

 

 

 

from sklearn import model_selection
# 将数据集拆分为训练集合测试集
Predictors = mushrooms.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(mushrooms[Predictors], mushrooms['type'], 
                                                                 test_size = 0.25, random_state = 10)

from sklearn import naive_bayes
from sklearn import metrics
import seaborn as sns
import matplotlib.pyplot as plt
# 构建多项式贝叶斯分类器的“类”
mnb = naive_bayes.MultinomialNB()
# 基于训练数据集的拟合
mnb.fit(X_train, y_train)
# 基于测试数据集的预测
mnb_pred = mnb.predict(X_test)
# 构建混淆矩阵
cm = pd.crosstab(mnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()

# 模型的预测准确率
print('模型的准确率为：\n',metrics.accuracy_score(y_test, mnb_pred))
print('模型的评估报告：\n',metrics.classification_report(y_test, mnb_pred))

 

伯努利贝叶斯分类器

适用于自变量为二元值的情况 

 

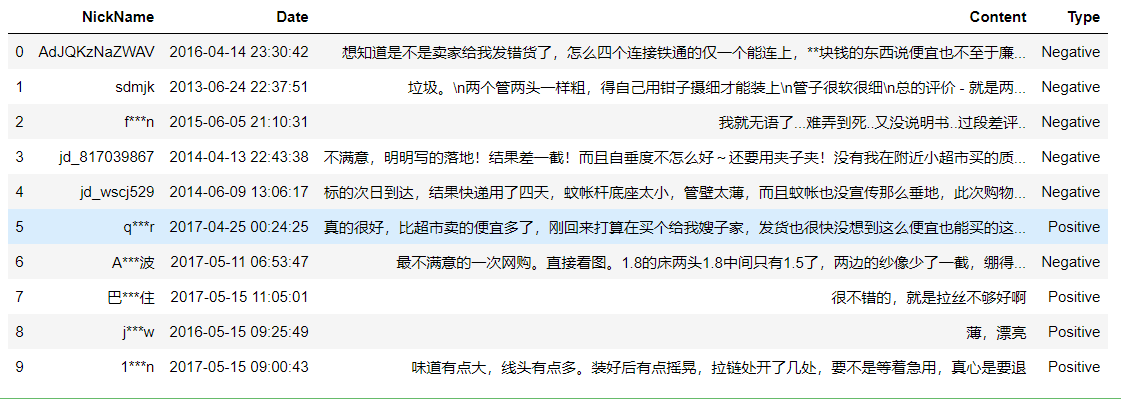
import pandas as pd
# 读入评论数据
evaluation = pd.read_excel(r'Contents.xlsx',sheet_name=0)
# 查看数据前10行
evaluation.head(10)

 

 

 

# 运用正则表达式，将评论中的数字和英文去除
evaluation.Content = evaluation.Content.str.replace('[0-9a-zA-Z]','')
evaluation.head()

 

 

 

 

 

 

# !pip3 install jieba
# !pip install jieba
# 导入第三方包
import jieba

# 加载自定义词库
jieba.load_userdict(r'all_words.txt')

# 读入停止词
with open(r'mystopwords.txt', encoding='UTF-8') as words:
    stop_words = [i.strip() for i in words.readlines()]

# 构造切词的自定义函数，并在切词过程中删除停止词
def cut_word(sentence):
    words = [i for i in jieba.lcut(sentence) if i not in stop_words]
    # 切完的词用空格隔开
    result = ' '.join(words)
    return(result)
# 对评论内容进行批量切词
words = evaluation.Content.apply(cut_word)
# 前5行内容的切词效果
words[:5]

 

# 导入第三方包
from sklearn.feature_extraction.text import CountVectorizer
# 计算每个词在各评论内容中的次数，并将稀疏度为99%以上的词删除
counts = CountVectorizer(min_df = 0.01)
# 文档词条矩阵
dtm_counts = counts.fit_transform(words).toarray()
# 矩阵的列名称
columns = counts.get_feature_names()
# 将矩阵转换为数据框--即X变量
X = pd.DataFrame(dtm_counts, columns=columns)
# 情感标签变量
y = evaluation.Type
X.head()

 

 

 

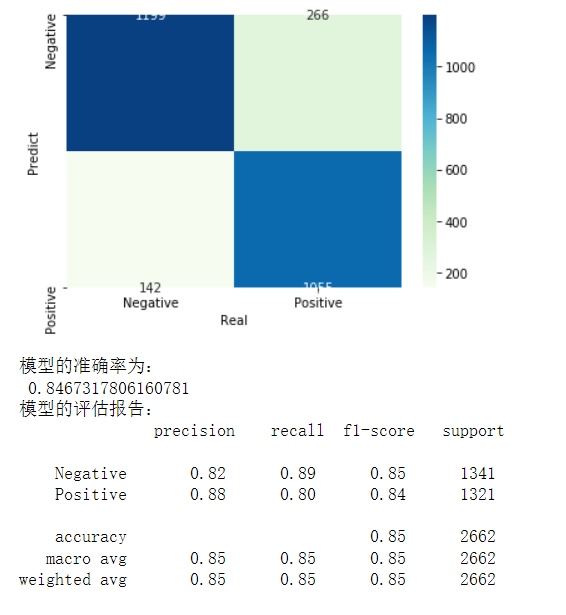
from sklearn import model_selection
from sklearn import naive_bayes
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns
# 将数据集拆分为训练集和测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.25, random_state=1)
# 构建伯努利贝叶斯分类器
bnb = naive_bayes.BernoulliNB()
# 模型在训练数据集上的拟合
bnb.fit(X_train,y_train)
# 模型在测试数据集上的预测
bnb_pred = bnb.predict(X_test)
# 构建混淆矩阵
cm = pd.crosstab(bnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()

# 模型的预测准确率
print('模型的准确率为：\n',metrics.accuracy_score(y_test, bnb_pred))
print('模型的评估报告：\n',metrics.classification_report(y_test, bnb_pred))

 

 

 

 

SVM模型

超平面的概念

将样本划分成不同的类别（三种表现形式：点、线、面）

 

超平面最优解

1.先随机选择一条直线

2.分布计算两边距离直线最短的点距离 取更小的距离

3.以该距离左右两边做分隔带

4.一次执行上述三个步骤得出N多个分隔带 最优的就是分隔带最宽的

 

线性可分与非线性可分

线性可分：简单地理解为就是一条直线划分类别

非线性可分：一条直线无法直接划分 需要提升一个维度

 

核函数：高斯核函数>>>>：支持无穷维度

 

# 读取外部数据
letters = pd.read_csv(r'letterdata.csv')
# 数据前5行
letters.head()

# 将数据拆分为训练集和测试集
predictors = letters.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(letters[predictors], letters.letter, 
                                                                 test_size = 0.25, random_state = 1234)

# 选择线性可分SVM模型
linear_svc = svm.LinearSVC()
# 模型在训练数据集上的拟合
linear_svc.fit(X_train,y_train)

# 模型在测试集上的预测
pred_linear_svc = linear_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test, pred_linear_svc)

# 选择非线性SVM模型
nolinear_svc = svm.SVC(kernel='rbf')
# 模型在训练数据集上的拟合
nolinear_svc.fit(X_train,y_train)

# 模型在测试集上的预测
pred_svc = nolinear_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test,pred_svc)

 

K均值聚类

k值的求解（表示分成几类）

1.拐点法

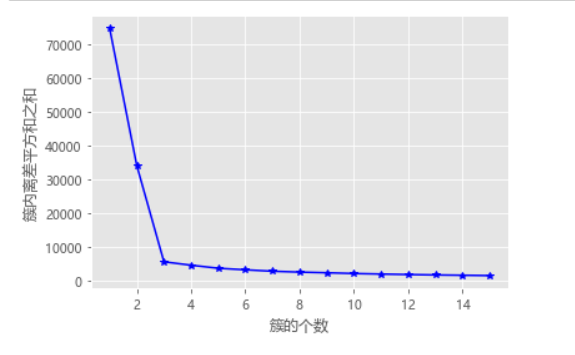
计算不同k值下类别中离差平方和（看斜率的变化，越明显越好）

2.轮廓系数法

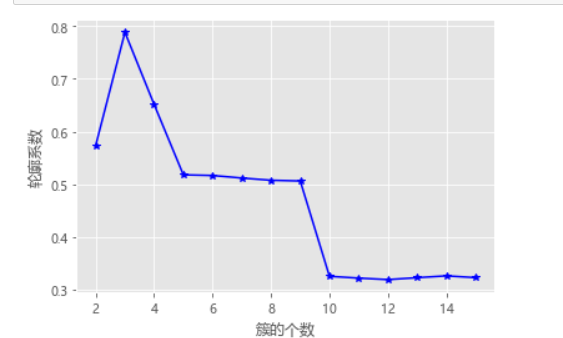
计算轮廓系数（看大小越大越好）

 

# 导入第三方包
import pandas as pd
import numpy as np  
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import metrics

# 随机生成三组二元正态分布随机数 
np.random.seed(1234)
mean1 = [0.5, 0.5]
cov1 = [[0.3, 0], [0, 0.3]]
x1, y1 = np.random.multivariate_normal(mean1, cov1, 1000).T

mean2 = [0, 8]
cov2 = [[1.5, 0], [0, 1]]
x2, y2 = np.random.multivariate_normal(mean2, cov2, 1000).T

mean3 = [8, 4]
cov3 = [[1.5, 0], [0, 1]]
x3, y3 = np.random.multivariate_normal(mean3, cov3, 1000).T

# 绘制三组数据的散点图
plt.scatter(x1,y1)
plt.scatter(x2,y2)
plt.scatter(x3,y3)
# 显示图形
plt.show()

 

 

 

 

 

# 构造自定义函数，用于绘制不同k值和对应总的簇内离差平方和的折线图
def k_SSE(X, clusters):
    # 选择连续的K种不同的值
    K = range(1,clusters+1)
    # 构建空列表用于存储总的簇内离差平方和
    TSSE = []
    for k in K:
        # 用于存储各个簇内离差平方和
        SSE = []
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        # 返回簇标签
        labels = kmeans.labels_
        # 返回簇中心
        centers = kmeans.cluster_centers_
        # 计算各簇样本的离差平方和，并保存到列表中
        for label in set(labels):
            SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
        # 计算总的簇内离差平方和 
        TSSE.append(np.sum(SSE))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制K的个数与GSSE的关系
    plt.plot(K, TSSE, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('簇内离差平方和之和')
    # 显示图形
    plt.show()

# 将三组数据集汇总到数据框中
X = pd.DataFrame(np.concatenate([np.array([x1,y1]),np.array([x2,y2]),np.array([x3,y3])], axis = 1).T)
# 自定义函数的调用
k_SSE(X, 15)

 

 

 

# 构造自定义函数，用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
    K = range(2,clusters+1)
    # 构建空列表，用于存储个中簇数下的轮廓系数
    S = []
    for k in K:
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        labels = kmeans.labels_
        # 调用字模块metrics中的silhouette_score函数，计算轮廓系数
        S.append(metrics.silhouette_score(X, labels, metric='euclidean'))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')    
    # 绘制K的个数与轮廓系数的关系
    plt.plot(K, S, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('轮廓系数')
    # 显示图形
    plt.show()
    
# 自定义函数的调用
k_silhouette(X, 15)

 

 

 

DBSCAN（密度）聚类

k均值聚类的两大特点

1.聚类效果容易受到异常样本点的影响

2.无法精准的将非球体样本进行合理的聚类

可以采用密度聚类解决上述两个缺点

 

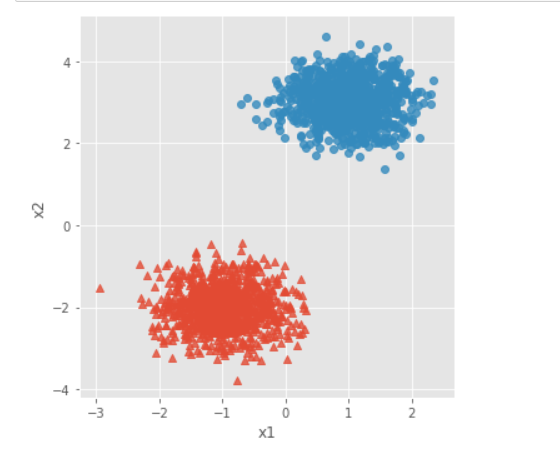
# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import cluster

# 模拟数据集
X,y = make_blobs(n_samples = 2000, centers = [[-1,-2],[1,3]], cluster_std = [0.5,0.5], random_state = 1234)
# 将模拟得到的数组转换为数据框，用于绘图
plot_data = pd.DataFrame(np.column_stack((X,y)), columns = ['x1','x2','y'])
# 设置绘图风格
plt.style.use('ggplot')
# 绘制散点图（用不同的形状代表不同的簇）
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o'],
           fit_reg = False, legend = False)
# 显示图形
plt.show()

 

 

 

 

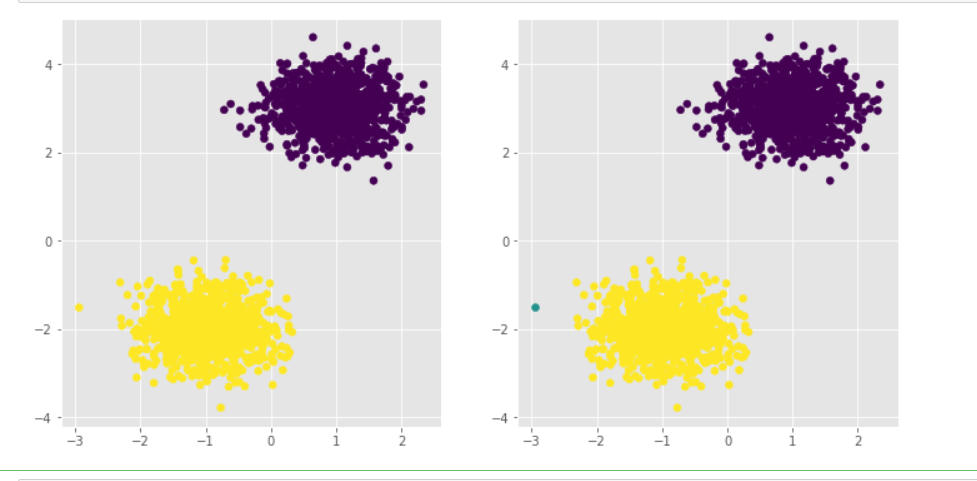
# 导入第三方模块
from sklearn import cluster
# 构建Kmeans聚类和密度聚类
kmeans = cluster.KMeans(n_clusters=2, random_state=1234)
kmeans.fit(X)
dbscan = cluster.DBSCAN(eps = 0.5, min_samples = 10)
dbscan.fit(X)
# 将Kmeans聚类和密度聚类的簇标签添加到数据框中
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_

# 绘制聚类效果图
# 设置大图框的长和高
plt.figure(figsize = (12,6))
# 设置第一个子图的布局
ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0))
# 绘制散点图
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
# 设置第二个子图的布局
ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1))
# 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致，通过序列的map“方法”对颜色作重映射)
ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:2,1:0}))
# 显示图形
plt.show()

 

 

 

 

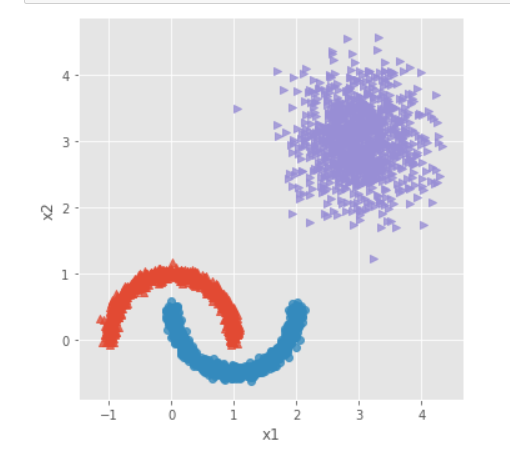
# 导入第三方模块
from sklearn.datasets.samples_generator import make_moons
# 构造非球形样本点
X1,y1 = make_moons(n_samples=2000, noise = 0.05, random_state = 1234)
# 构造球形样本点
X2,y2 = make_blobs(n_samples=1000, centers = [[3,3]], cluster_std = 0.5, random_state = 1234)
# 将y2的值替换为2(为了避免与y1的值冲突，因为原始y1和y2中都有0这个值)
y2 = np.where(y2 == 0,2,0)
# 将模拟得到的数组转换为数据框，用于绘图
plot_data = pd.DataFrame(np.row_stack([np.column_stack((X1,y1)),np.column_stack((X2,y2))]), columns = ['x1','x2','y'])

# 绘制散点图（用不同的形状代表不同的簇）
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o','>'],
           fit_reg = False, legend = False)
# 显示图形
plt.show()

 

 

 

 

 

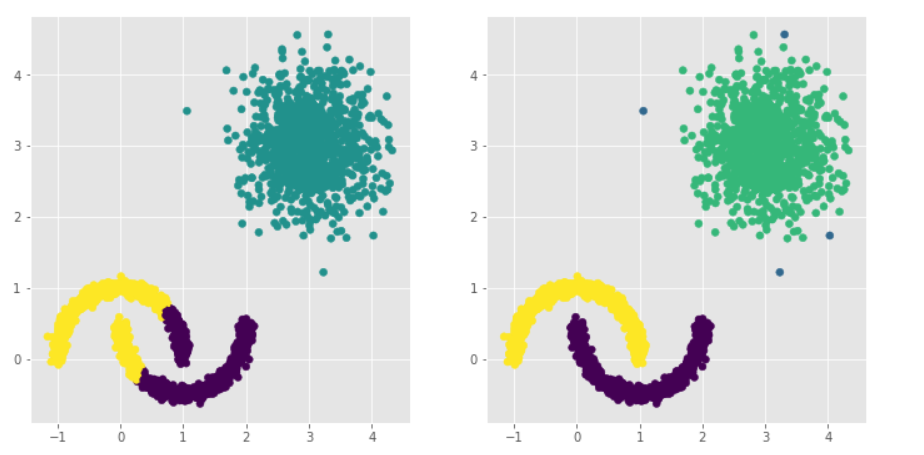
# 构建Kmeans聚类和密度聚类
kmeans = cluster.KMeans(n_clusters=3, random_state=1234)
kmeans.fit(plot_data[['x1','x2']])
dbscan = cluster.DBSCAN(eps = 0.3, min_samples = 5)
dbscan.fit(plot_data[['x1','x2']])
# 将Kmeans聚类和密度聚类的簇标签添加到数据框中
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_

# 绘制聚类效果图
# 设置大图框的长和高
plt.figure(figsize = (12,6))
# 设置第一个子图的布局
ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0))
# 绘制散点图
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
# 设置第二个子图的布局
ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1))
# 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致，通过序列的map“方法”对颜色作重映射)
ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:0,1:3,2:2}))
# 显示图形
plt.show()

 

 

 

 

核心概念

核心对象：内部含有至少大于等于最少样本点的样本

非核心对象：内部少于最少样本点的样本

直接密度可达：在核心对象内部的样本点到核心对象的距离

密度可达：多个直接密度可达链接了多个核心对象（首尾点密度可达）

密度相连：两边的点由中间的核心对象分别密度可达

 

GBDT模型

Adaboost算法（既可以解决分类问题也可以解决预测问题）

由多颗基础决策树组成 并且这些决策树彼此之间由先后关系

SMOTE算法

通过算法将比例较少的数据样本扩大

 

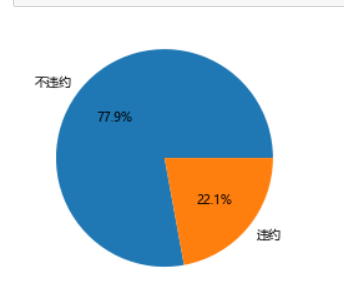
# 导入第三方包
import pandas as pd
import matplotlib.pyplot as plt

# 读入数据
default = pd.read_excel(r'default of credit card.xls')

# 数据集中是否违约的客户比例
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 统计客户是否违约的频数
counts = default.y.value_counts()
# 绘制饼图
plt.pie(x = counts, # 绘图数据
        labels=pd.Series(counts.index).map({0:'不违约',1:'违约'}), # 添加文字标签
        autopct='%.1f%%' # 设置百分比的格式，这里保留一位小数
       )
# 显示图形
plt.show()

 

 

 

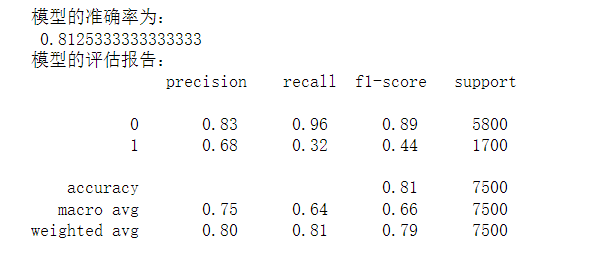
# 将数据集拆分为训练集和测试集
# 导入第三方包
from sklearn import model_selection
from sklearn import ensemble
from sklearn import metrics

# 排除数据集中的ID变量和因变量，剩余的数据用作自变量X
X = default.drop(['ID','y'], axis = 1)
y = default.y
# 数据拆分
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.25, random_state = 1234)

# 构建AdaBoost算法的类
AdaBoost1 = ensemble.AdaBoostClassifier()
# 算法在训练数据集上的拟合
AdaBoost1.fit(X_train,y_train)
# 算法在测试数据集上的预测
pred1 = AdaBoost1.predict(X_test)

# 返回模型的预测效果
print('模型的准确率为：\n',metrics.accuracy_score(y_test, pred1))
print('模型的评估报告：\n',metrics.classification_report(y_test, pred1))

 

 

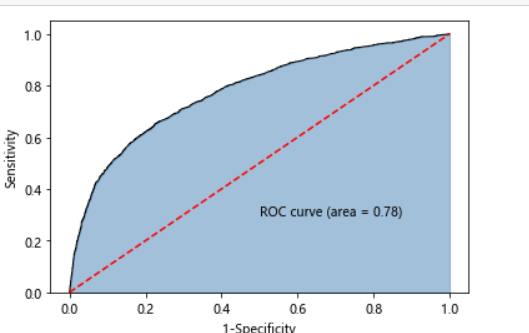
# 计算客户违约的概率值，用于生成ROC曲线的数据
y_score = AdaBoost1.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

 

 

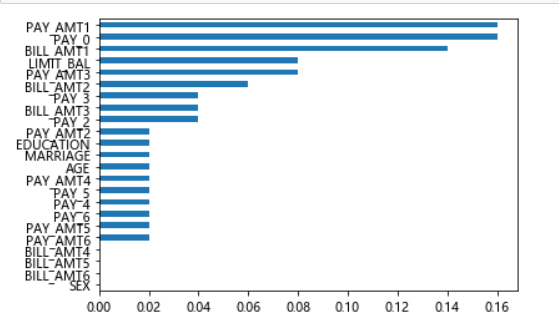
# 自变量的重要性排序
importance = pd.Series(AdaBoost1.feature_importances_, index = X.columns)
importance.sort_values().plot(kind = 'barh')
plt.show()