多元线性回归模型

一元线性回归模型

分析两个变量之间知否存在明显的线性关系

 

一元线性回归

公式：y=ax+b

多元线性回归

公式：y=a1x+a2x+a3x+......b

 

数据符号网站

 

 

 

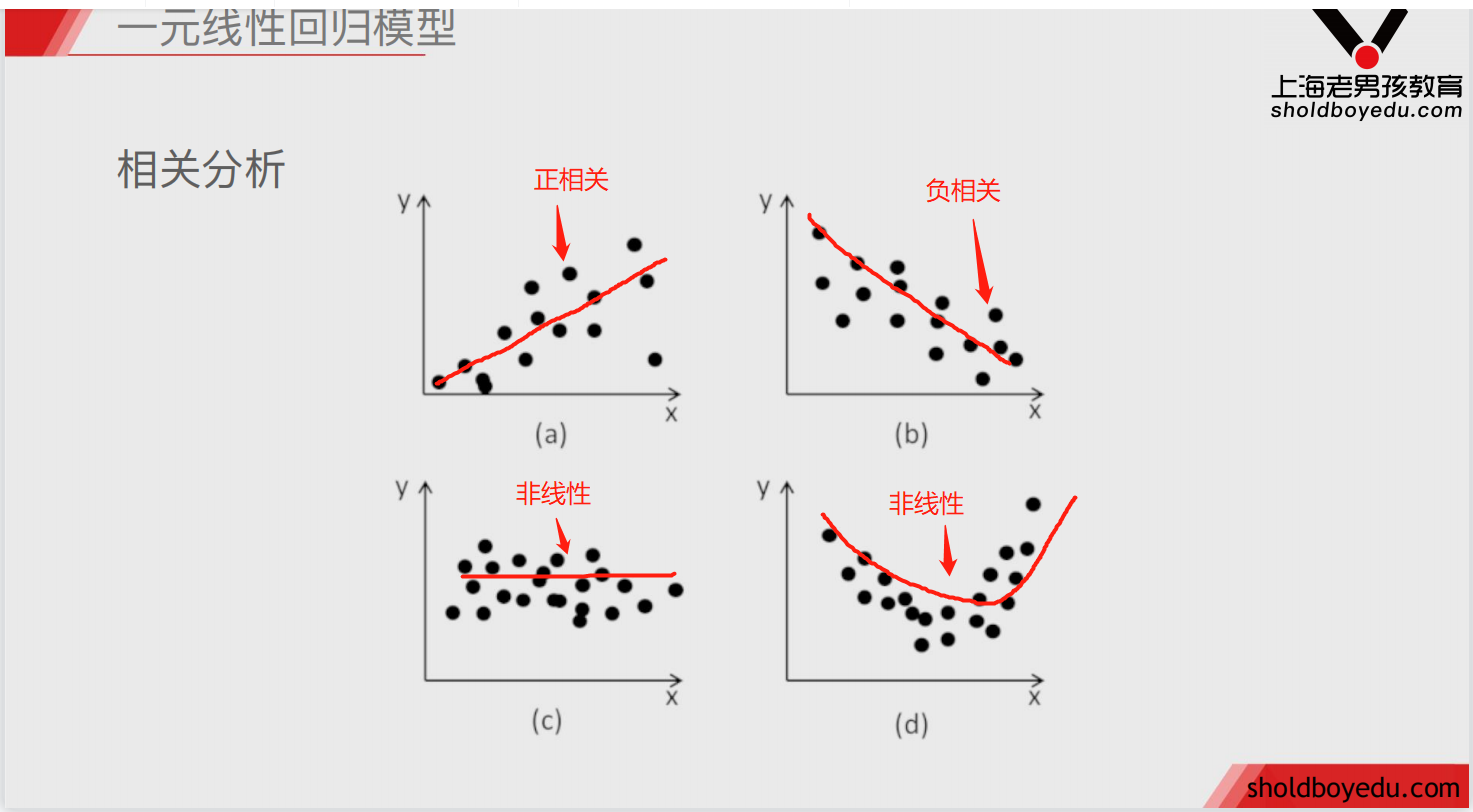
散点图

看不出线性关系的不能说没有关系只能说没有线性关系

 

 

 

 

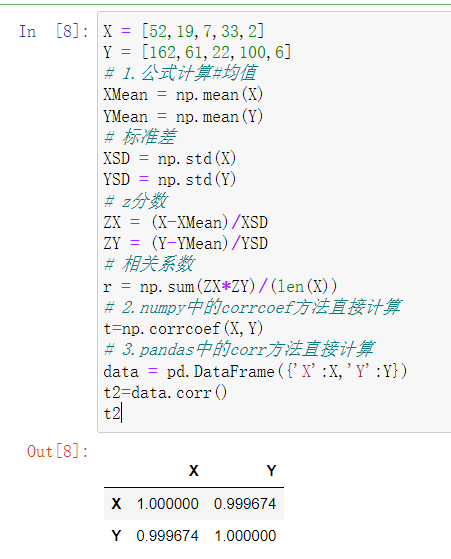
公式计算

　　大于等于0.8表示高度相关（存在明显的线性关系）

　　绝对值大于0.5小于等于0.8表示中度相关（存在一定的线性关系）

　　绝对值大于等于0.3小于0.5表示若相关（存在较弱的线性关系）

　　绝对值小于0.3表示几乎不相关（表示基本没有线性关系，需要注意这里的不相干指的是没有线性关系，两者之间可能存在其他关系）

import numpy
import pandas
X = [52,19,7,33,2]
Y = [162,61,22,100,6]
# 1.公式计算#均值
XMean = numpy.mean(X)
YMean = numpy.mean(Y)
# 标准差
XSD = numpy.std(X)
YSD = numpy.std(Y)
# z分数
ZX = (X-XMean)/XSD
ZY = (Y-YMean)/YSD  
# 相关系数
r = numpy.sum(ZX*ZY)/(len(X))
# 2.numpy中的corrcoef方法直接计算
t=numpy.corrcoef(X,Y)
# 3.pandas中的corr方法直接计算
data = pandas.DataFrame({'X':X,'Y':Y})
t2=data.corr()

 

 

 

训练集与测试集

训练集用于模型的训练穿件 测试集用于模型的测试实验

一般情况下训练集占总数据的80%、测试集占总数20%

哑变量

在生成算法模型的时候有些变量可能并不是数字无法直接带入公式计算

此时可以构造变量>>>>C（state）

自变量与应变量

模型中的x为自变量，y为应变量

a为模型的截距项，b为模型的斜率项，ε为模型的误差项

误差项ε的存在主要是为了平衡等号两边的值，通常被称为

 

自定义哑变量

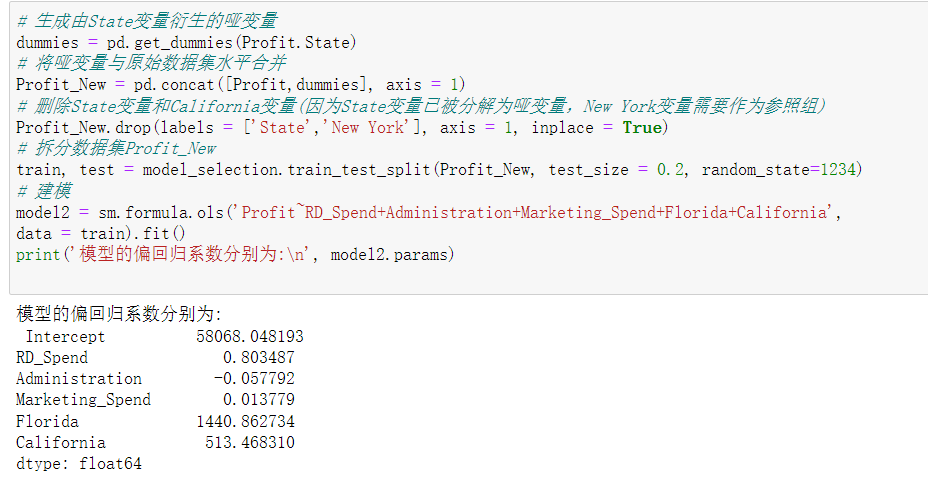
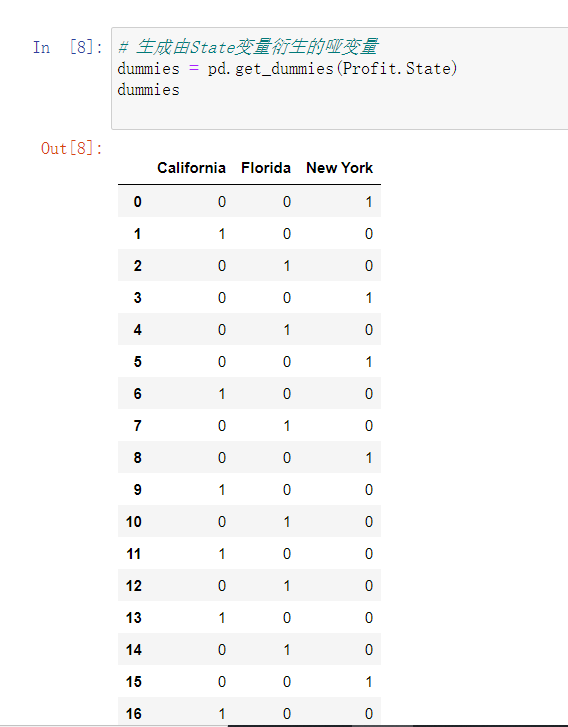
生成有state变量衍生的哑变量

dummies = pd.get_dummies(Profit.State)

 

 

将哑变量与原始数据集水平合并

Profit_New = pd.concat([Profit,dummies], axis = 1)

删除State变量和California变量（因为State变量已被分解为哑变量，New York变量需要作为参照组）

Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)

拆分数据集Profit_New

train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)

建模

model2 = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+Florida+California', data = train).fit()
print('模型的偏回归系数分别为：\n', model2.params)