机器学习：K-近邻算法（KNN）

机器学习：K-近邻算法（KNN）

一、KNN算法概述

KNN作为一种有监督分类算法，是最简单的机器学习算法之一，顾名思义，其算法主体思想就是根据距离相近的邻居类别，来判定自己的所属类别。算法的前提是需要有一个已被标记类别的训练数据集，具体的计算步骤分为一下三步：
1、计算测试对象与训练集中所有对象的距离，可以是欧式距离、余弦距离等，比较常用的是较为简单的欧式距离；
2、找出上步计算的距离中最近的K个对象，作为测试对象的邻居；
3、找出K个对象中出现频率最高的对象，其所属的类别就是该测试对象所属的类别。
 

二、算法优缺点

1、优点

思想简单，易于理解，易于实现，无需估计参数，无需训练；
适合对稀有事物进行分类；
特别适合于多分类问题。

2、缺点

懒惰算法，进行分类时计算量大，要扫描全部训练样本计算距离，内存开销大，评分慢；
当样本不平衡时，如其中一个类别的样本较大，可能会导致对新样本计算近邻时，大容量样本占大多数，影响分类效果；
可解释性较差，无法给出决策树那样的规则。

三、注意问题

1、K值的设定
K值设置过小会降低分类精度；若设置过大，且测试样本属于训练集中包含数据较少的类，则会增加噪声，降低分类效果。
通常，K值的设定采用交叉检验的方式（以K=1为基准）
经验规则：K一般低于训练样本数的平方根。
2、优化问题
压缩训练样本；
确定最终的类别时，不是简单的采用投票法，而是进行加权投票，距离越近权重越高。
 

四、python中scikit-learn对KNN算法的应用

  
#KNN调用
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target
np.unique(iris_y)
# Split iris data in train and test data
# A random permutation, to split the data randomly
np.random.seed(0)
# permutation随机生成一个范围内的序列
indices = np.random.permutation(len(iris_X))
# 通过随机序列将数据随机进行测试集和训练集的划分
iris_X_train = iris_X[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_X_test  = iris_X[indices[-10:]]
iris_y_test  = iris_y[indices[-10:]]
# Create and fit a nearest-neighbor classifier
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(iris_X_train, iris_y_train) 
 
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=5, p=2,
           weights='uniform')
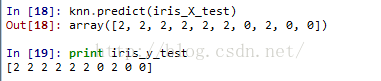
knn.predict(iris_X_test)
print iris_y_test

 

 
KNeighborsClassifier方法中含有8个参数（以下前两个常用）：
n_neighbors : int, optional (default = 5)：K的取值，默认的邻居数量是5；
weights：确定近邻的权重，“uniform”权重一样，“distance”指权重为距离的倒数，默认情况下是权重相等。也可以自己定义函数确定权重的方式；
algorithm : {'auto', 'ball_tree', 'kd_tree', 'brute'},optional：计算最近邻的方法，可根据需要自己选择；
leaf_size : int, optional (default = 30)
 |      Leaf size passed to BallTree or KDTree.  This can affect the
 |      speed of the construction and query, as well as the memory
 |      required to store the tree.  The optimal value depends on the
 |      nature of the problem.
 |  
 |  metric : string or DistanceMetric object (default = 'minkowski')
 |      the distance metric to use for the tree.  The default metric is
 |      minkowski, and with p=2 is equivalent to the standard Euclidean
 |      metric. See the documentation of the DistanceMetric class for a
 |      list of available metrics.
 |  
 |  p : integer, optional (default = 2)
 |      Power parameter for the Minkowski metric. When p = 1, this is
 |      equivalent to using manhattan_distance (l1), and euclidean_distance
 |      (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used.
 |  
 |  metric_params: dict, optional (default = None)
 |      additional keyword arguments for the metric function.


输出结果：
 
结果一致。

 --------------------------------------------------------------------------------------------------------------------------------------

 

一、简介

简单地说，k-近邻算法采用测量不同特征值之间的距离方法进来分类 
特点：

  • 优点：精度高、对异常值不敏感、无数据输入假定
  • 缺点：计算复杂度高、空间复杂度高
  • 适用数据范围：数值型和标称型

k-近邻算法称为kNN，它的工作原理是：存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们只选择样本数据集中前κ个最相似的数据，这就是k-近邻算法中κ的出处。通常κ是不大于20的整数。最后，选择κ个最相似数据出现次数最多的分类，作为新数据的分类。

二、示例

电影分类。 
样本数据：

电影名称打斗镜头接吻镜头电影类型
California Man 3 104 爱情片
He’s Not Really into Dudes 2 100 爱情片
Beautiful woman 1 81 爱情片
Kevin Longblade 101 10 动作片
Robo Slayer 3000 99 5 动作片
Amped II 98 22 动作片
? 18 90 未知

如果我们计算出已知电影与未知电影的距离：

电影名称与未知电影的距离
California Man 20.5
He’s Not Really into Dudes 18.7
Beautiful woman 19.2
Kevin Longblade 115.3
Robo Slayer 3000 117.4
Amped II 118.9

按照距离递增排序，可以找到k个距离最近的电影。假定k=3，则三个最靠近的电影依次是：

  1. He’s Not Really into Dudes
  2. Beautiful woman
  3. California Man

kNN按照距离最近的三部电影的类型，决定未知电影的类型——爱情片。

三、Python操作

1. 使用Python导入数据

from numpy import *
import operator

def createDataSet():
#用来创建数据集和标签
    group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group , labels

 

这里有4组数据，每组数据有两个我们已知的属性或者特征值。向量labels包含了每个数据点的标签信息，labels包含的元素个数等于group矩阵行数。这里将数据点（1,1.1）定义为类A，数据点（0,0.1）定义为类B。为了说明方便，例子中的数值是任意选择的，并没有给出轴标签。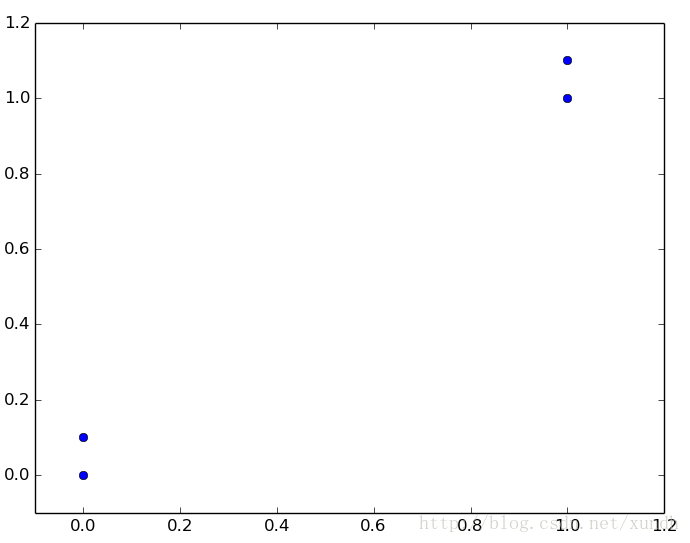 
这里写图片描述 
kNN，带有4个数据点的简单例子。

2. 实施kNN分类算法

代码流程为： 
计算已知类别数据集中的每个点依次执行以下操作

  1. 计算已知类别数据集中的点与当前点之间的距离
  2. 按照距离递增次序排序
  3. 选择与当前点距离最小的κ个点
  4. 确定前κ个点所在类别的出现概率
  5. 返回前κ个点出现频率最高的类别作为当前点的预测分类

classify0函数：

def classify0(inX,dataSet,labels,k):
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX,(dataSetSize,1)) - dataSet
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5
    sortedDistIndicies = distances.argsort()
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

 

参数说明：

  • inX：用于分类的输入向量
  • dataSet：输入的训练样本集
  • labels：标签向量
  • k：用于选择最近邻居的数目

其中标签向量的元素数目和矩阵dataSet的行数相同。程序使用的是欧氏距离公式，计算向量xA与xB之间的距离： 

 
d=(xA0−xB0)2+(xA1−xB1)2−−−−−−−−−−−−−−−−−−−−−−−−√d=(xA0−xB0)2+(xA1−xB1)2


计算完距离后，对数据按照从小到大排序，确认前k个距离最小元素民在的主要分类。输入k总是正整数；最后，将classCount字典分解为元组列表，然后使用程序第二行导入运算符模块的itemgetter方法，按照第二个元素的次序对元组进行排序，最后返回发生频率最高的元素标签。 
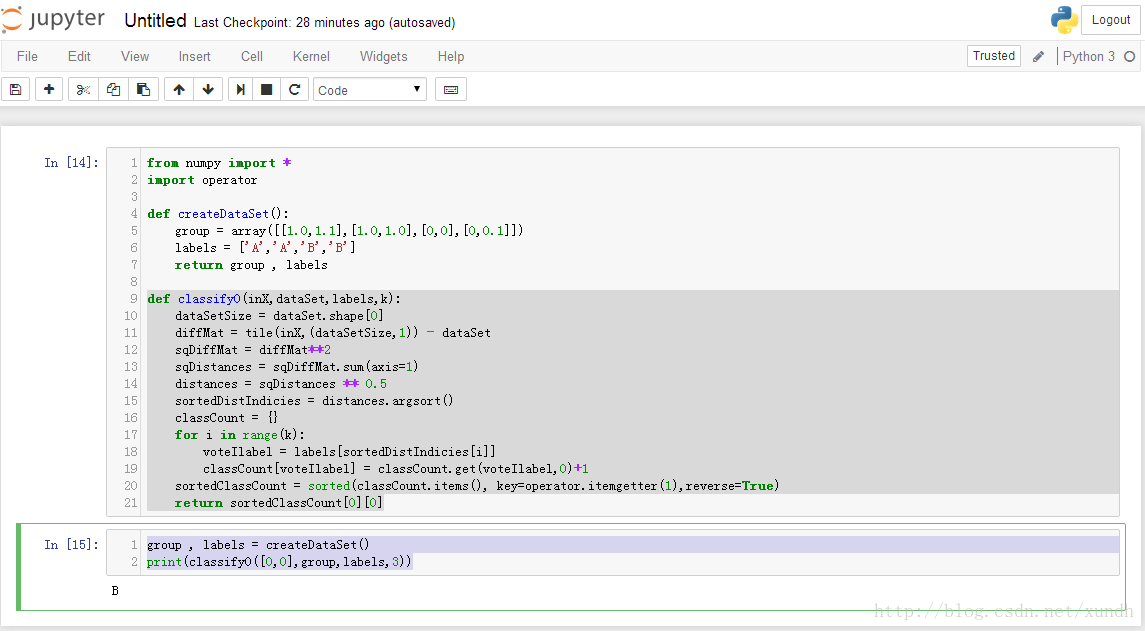
运行测试：

 

group , labels = createDataSet()
print(classify0([0,0],group,labels,3))

 

这里写图片描述

3. 如何测试分类器

错误率是评估常用方法，完美的错误率为0，最差错误率是1.0。

四、示例：使用kNN改进约会网站的配对效果

1.使用Matplotlib创建散点图

准备一份样本数据。

每年获得的飞行常客里程数 玩视频游戏所耗时间百分比 每周消费的冰淇淋公升数
40920   8.326976    0.953952    3
14488   7.153469    1.673904    2
26052   1.441871    0.805124    1
75136   13.147394   0.428964    1
38344   1.669788    0.134296    1
...

 

代码：

from numpy import *
import operator

def classify0(inX,dataSet,labels,k):
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX,(dataSetSize,1)) - dataSet
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5
    sortedDistIndicies = distances.argsort()
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

def file2matrix(filename):
    fr = open(filename)
    arrayOfLines = fr.readlines()
    numberOfLines = len(arrayOfLines)
    returnMat = zeros((numberOfLines,3))
    classLabelVector = []
    index = 0
    for line in arrayOfLines:
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3]
        classLabelVector.append(int(listFromLine[-1]))
        index += 1

datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')

import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:,1],datingDataMat[:,2])
plt.show()

 

获得的散点图示例： 
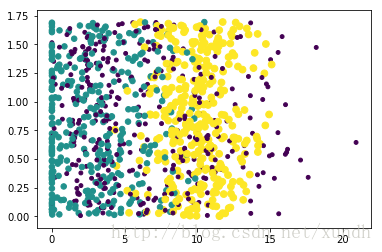
这里写图片描述

样本数据可以在网上通过搜索”datingTestSet2.txt”获得。这里散点图使用datingDataMat矩阵的第二、第三列数据，分别表示特征值“玩视频游戏所耗时间百分比”和“每周所消费的冰淇淋公升数”。

由于没有使用样本分类的特征值，在图上很难看出任何有用的数据模式信息。一般来说，可以采用色彩或其他的记号来标记不同样本分类，以便更好地理解数据信息。进行这样的修改：

ax.scatter(datingDataMat[:,1],datingDataMat[:,2] ,15.0*array(datingLabels),15.0*array(datingLabels))

 

这里写图片描述

利用变量datingLabels存储的类标签属性，在散点图上绘制了色彩不等、尺寸不同的点。

2.准备数据：归一化数值

归一化数值将不同取值范围的特征值进行数值归一化，如将取值范围处理为0到1或者-1到1之间。通过下面公式可以将取值范围特征值转化为0到1区间内的值：

newValue=(oldValue−min)/(max−min)

 

其中min和max分别是数据集中的最小特征值和最大特征值。虽然改变数值取值范围增加了分类器的复杂度，但为了得到准确结果，我们必须这样做。下面autoNorm()函数实现归一化:

def autoNorm(dataSet):
      minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals -minVals
    nromDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals,(m,1))
    normDataSet = normDataSet/tile(ranges,(m,1))
    return normDataSet , ranges , minVals

normMat , ranges , minVals = autoNorm(datingDataMat)

 

3.测试算法

通常我们使用已有数据的90%作为训练样本来训练分类器，而使用10%的数据去测试分类器，检测分类器的正确率。创建一个测试函数：

def datingClassTest():
    hoRatio = 0.10
    datingDataMat , datingLabels = file2matrix('datingTestSet.txt')
    normMat,ranges,minVals = autoNorm(datingDataMat)
    m = normMat.shape[0]
    numTestVecs = int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],\
                                    datingLabels[numTestVecs:m],3)
        print ("the classifier came back with : %d,the real answer is :%d"\
              %(classifierResult,datingLabels[i]))
        if(classifierResult != datingLabels[i]):errorCount += 1.0
    print ("the total error rate is :%f" % (errorCount / float(numTestVecs)))

 

使用

normMat , ranges , minVals = autoNorm(datingDataMat)
datingClassTest()

 

4.补全程序，实现完整功能

def classifyPerson():
    resultList = ['not at all','in small doses','in large doses']
    percentTats = float(input("percetage of time spent playing video games?"))
    ffMiles = float(input("frequent flier miles earned per year?"))
    iceCream = float(input("listers of ice cream consumed per year?"))
    datinDataMat,datingLabels = file2matrix('datingTestSet2.txt')
    normMat,ranges ,minVals=autoNorm(datingDataMat)
    inArr = array([ffMiles,percentTats,iceCream])
    classifierResult = classify0((inArr-minVals)/ranges,normMat,datingLabels,3)
    print ("You will probably like this person:",resultList[classifierResult - 1])

classifyPerson()

 

运行结果示例： 
这里写图片描述

 

==========================================================================

 

一.基本思想

K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。如下面的图：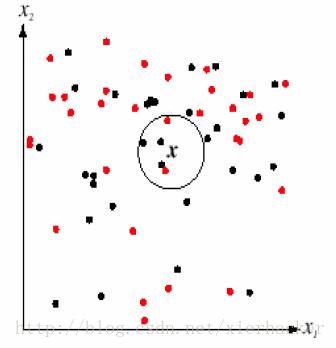 
这里写图片描述 
通俗一点来说，就是找最“邻近”的伙伴，通过这些伙伴的类别来看自己的类别。比如以性格和做过的事情为判断特征，和你最邻近的10个人中（这里暂且设k=10），有8个是医生，有2个是强盗。那么你是医生的可能性更加大，就把你划到医生的类别里面去，这就算是K近邻的思想。 
K近邻思想是非常非常简单直观的思想。非常符合人类的直觉，易于理解。 
至此，K近邻算法的核心思想就这么多了。 
K值选择,距离度量,分类决策规则是K近邻法的三个基本要素. 
从K近邻的思想可以知道，K近邻算法是离不开对于特征之间“距离”的表征的.

二.实战

这一部分的数据集《机器学习实战》中的KNN约会分析，代码按照自己的风格改了一部分内容。 

首先是读取数据部分(data.py)：

import numpy as np 

def creatData(filename):
    #打开文件,并且读入整个文件到一个字符串里面
    file=open(filename)
    lines=file.readlines()
    sizeOfRecord=len(lines)

    #开始初始化数据集矩阵和标签
    group=np.zeros((sizeOfRecord,3))
    labels=[]
    row=0
    #这里从文件读取存到二维数组的手法记住
    for line in lines:
        line=line.strip()
        tempList=line.split('\t')
        group[row,:]=tempList[:3]

        labels.append(tempList[-1])
        row+=1
    return group,labels

 

然后是KNN算法的模块：KNN.py

import numpy as np 
#分类函数(核心)
def classify(testdata,dataset,labels,k):
    dataSize=dataset.shape[0]
    testdata=np.tile(testdata,(dataSize,1))
    #计算距离并且按照返回排序后的下标值列表
    distance=(((testdata-dataset)**2).sum(axis=1))**0.5
    index=distance.argsort()

    classCount={}
    for i in range(k):
        label=labels[index[i]]
        classCount[label]=classCount.get(label,0)+1

    sortedClassCount=sorted(list(classCount.items()),
        key=lambda d:d[1],reverse=True)

    return sortedClassCount[0][0]


#归一化函数(传入的都是处理好的只带数据的矩阵)
def norm(dataset):
    #sum/min/max函数传入0轴表示每列,得到单行M列的数组
    minValue=dataset.min(0)
    maxValue=dataset.max(0)

    m=dataset.shape[0]
    return (dataset-np.tile(minValue,(m,1)))/np.tile(maxValue-minValue,(m,1))


#测试函数
def classifyTest(testdataset,dataset,dataset_labels,
                testdataset_labels,k):
    sampleAmount=testdataset.shape[0]

    #归一化测试集合和训练集合
    testdataset=norm(testdataset)
    dataset=norm(dataset)
    #测试
    numOfWrong=0
    for i in range(sampleAmount):
        print("the real kind is:",testdataset_labels[i])
        print("the result kind is:",
            classify(testdataset[i],dataset,dataset_labels,k))
        if testdataset_labels[i]==classify(testdataset[i],
                                    dataset,dataset_labels,k):
            print("correct!!")
        else:
            print("Wrong!!")
            numOfWrong+=1
        print()

    print(numOfWrong)

 

画图模块(drawer.py)：

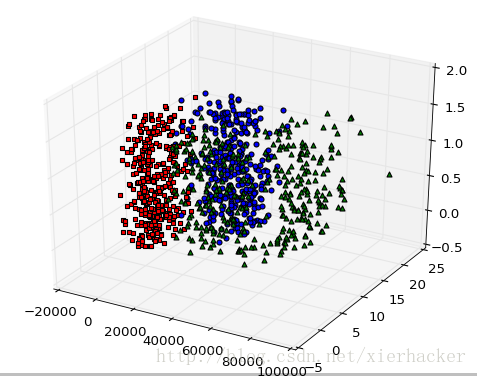
import matplotlib.pyplot as plt
import numpy as np 
from mpl_toolkits.mplot3d import Axes3D
import data 

def drawPlot(dataset,labels):
    fig=plt.figure(1)
    ax=fig.add_subplot(111,projection='3d')
    for i in range(dataset.shape[0]):
        x=dataset[i][0]
        y=dataset[i][1]
        z=dataset[i][2]
        if labels[i]=='largeDoses':
            ax.scatter(x,y,z,c='b',marker='o')
        elif labels[i]=='smallDoses':
            ax.scatter(x,y,z,c='r',marker='s')
        else:
            ax.scatter(x,y,z,c='g',marker='^')
    plt.show()

 

测试模块（run.py）

import data
import KNN 
import drawer

#这里测试数据集和训练数据集都是采用的同一个数据集
dataset,labels=data.creatData("datingTestSet.txt")
testdata_set,testdataset_labels=data.creatData("datingTestSet.txt")

print(type(dataset[0][0]))
#测试分类效果。K取得是10
KNN.classifyTest(testdata_set,dataset,labels,testdataset_labels,10)

#画出训练集的分布
drawer.drawPlot(dataset,labels)

 

结果： 
这里写图片描述

三.优缺点分析

从上面的代码可以看到，K近邻法并不具有显式的学习过程,你必须先把数据集存下来，然后类似于比对的来作比较。K近邻法实际上是利用训练数据集对特征向量空间进行划分,并且作为其分类的模型 
优点：

多数表决规则等价于经验风险最小化. 
精度高,对异常值不敏感,无数据输入假定

缺点：

K值选择太小,意味着整体模型变得复杂,容易发生过拟合.但是K值要是选择过大的话,容易忽略实例中大量有用的信息,也不可取.一般是先取一个比较小的数值,通常采用交叉验证的方式来选取最优的K值. 
计算复杂度高,空间复杂度高

 

本文摘自：https://blog.csdn.net/xundh/article/details/73611249

　　　　　https://blog.csdn.net/helloworld6746/article/details/50817427

　　　　　https://blog.csdn.net/xierhacker/article/details/61914468

 

posted @ 2018-09-17 11:25  时间&煮雨~  阅读(9493)  评论(0)  编辑  收藏  举报