Sobel算子的数学基础
更准确的说法应该叫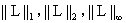
，即数值分析中的1-范数、2-范数、无穷范数。下面仅以二维空间中的两点
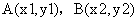为例。
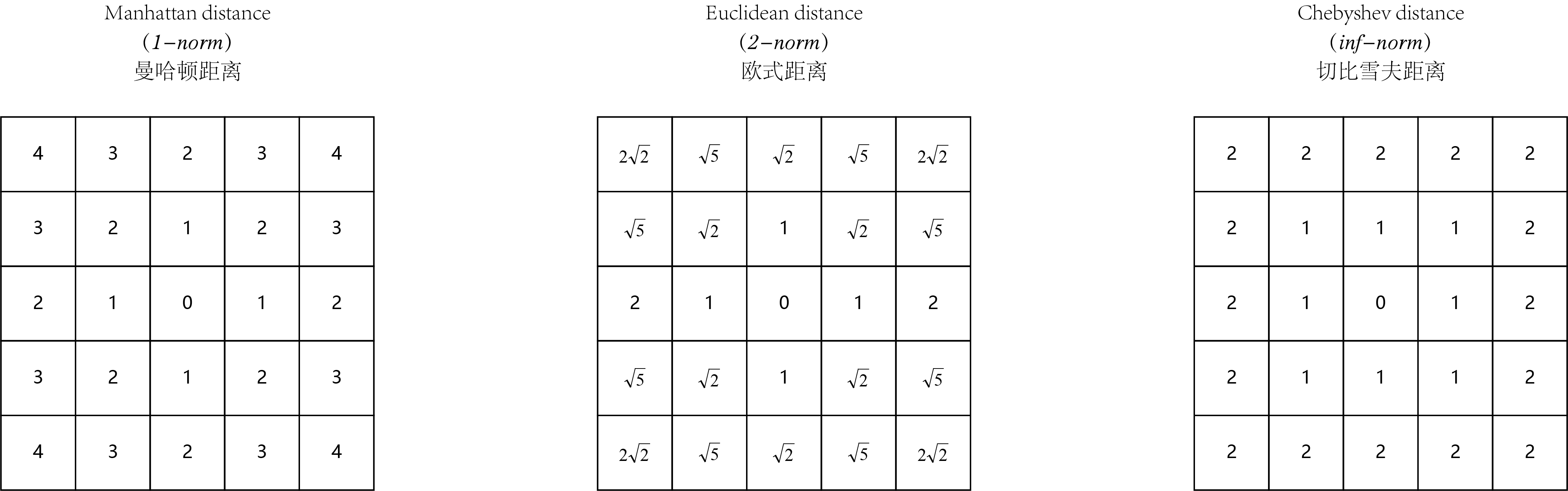
L1距离，曼哈顿距离（Manhattan distance）也称D4距离、城市街区距离（Cityblock distance）、出租车距离（Taxicab distance）、直线式距离（Rectilinear distance）或蛇形距离（Snake distance）
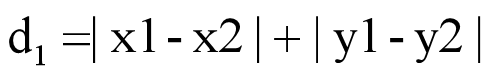
L2距离，欧式距离（Euclidean distance）
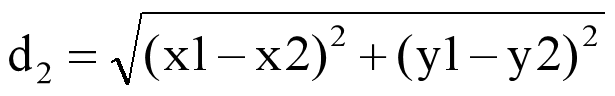
L-Inf距离，切比雪夫距离（Chebyshev distance）也称D8距离、棋盘距离（Chessboard distance）
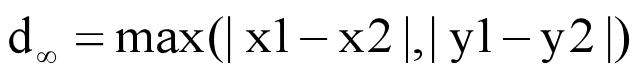
彭真明老师在Sobel算子的数学基础中阐述
Sobel算子考虑了水平、垂直和2个对角共计4个方向对的梯度加权求和，是一个3×3各向异性的梯度算子。
Sobel算子具有严格的数学基础，主要关键点在于：
1）笛卡尔网格（Cartesian grid）；
2）前向差分（Forward-difference）；
3）距离反比的4方向对梯度加权；
4）城市距离（City-block distance）。
大熊背在Sobel边缘检测算子数学原理再学习中认为
更正确的表述为：
1）笛卡尔网格（Cartesian grid）；
2）中心差分（Central-difference）；
3）由导数和对应的单位向量所定义的方向导数所构成的正交向量求和；
4）欧式距离（Euclidean distance）。
参考文献
【2】An Isotropic 3x3 Image Gradient Operator
【3】Sobel算子的数学基础
