JAVA浮点数计算精度丢失与解决方案
一、问题背景
近期公司项目开发过程中,犯了一个小错误,在使用java计算金额时,使用double直接使用加减乘除。代码评审时,同事指出浮点数会出现丢失进度的问题,自己深思了一下,还是自己不够细心,之前也知道浮点数会丢失精度,但是再开发过程中给忘记了,非常感谢同事的指出。让我有机会记录下,在此编写这篇文章用于记录下问题出现及其解决方案,加深自己的印象,后续不要再犯这样低级的错误了。也希望各位开发朋友看到后避免此问题,自己也是小白一个,如有写的错误的地方,还望各位大佬积极指出,谢谢!
二、JAVA浮点型知识回顾
float
float属于Java中的浮点型,也叫单精度浮点型,长度为4字节32bit,变量初始化默认值0.0f,包装类Float
1. float结构
包含三部分:符号位、指数位、尾数位
| 符号位(S) | 指数位(E) | 尾数位(M) | |
|---|---|---|---|
| 长度 | 1bit | 8bit | 23bit |
| 说明 | 0表示正数,1表示负数 | 格式为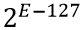 ,E值范围:(0,255),指数位取值:( ,E值范围:(0,255),指数位取值:(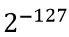 , ,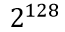 |
形式为1.M或0.M。其中当E=0时,取1.M,称为正规形式,当E!= 0时,取0.M,称为非正规形式 |
2. float取值
正规形式: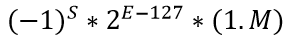
非正规形式:
根据上面公式很容易计算出float的取值范围为:
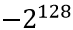
(最小值,当符号位S取1,指数位E取255)

(最大值,当符号位S取0,指数位E取255)
能取到其间的近似数据。
注意:根据指数位和尾数位的取值不同,还有很多特殊情况,如NAN,正无穷,负无穷,但平时基本不会用到,这里不再深入;同时由于是近似值,因此无法表示金额,表示金额建议使用BigDecimal
double
double属于Java中的浮点型,也叫双精度浮点型,长度为8字节64bit,变量初始化默认值0.0d,包装类Double
1. double结构
包含三部分:符号位、指数位、尾数位
| 符号位(S) | 指数位(E) | 尾数位(M) | |
|---|---|---|---|
| 长度 | 1bit | 11bit | 52bit |
| 说明 | 0表示正数,1表示负数 | 格式为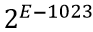 ,E值范围:(0,2047),指数位取值:( ,E值范围:(0,2047),指数位取值:(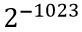 , , ) ) |
形式为1.M或0.M。其中当E=0时,取1.M,称为正规形式,当E!= 0时,取0.M,称为非正规形式 |
2. double取值
正规形式:
非正规形式:
根据上面公式很容易计算出double的取值范围为:

(最小值,当符号位S取1,指数位E取2047)
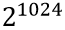
(最大值,当符号位S取0,指数位E取2047)
能取到其间的近似数据。
注意:根据指数位和尾数位的取值不同,还有很多特殊情况,如NAN,正无穷,负无穷,但平时基本不会用到,这里不再深入;同时由于是近似值,因此无法表示金额,表示金额建议使用BigDecimal
三、问题解析
float和double类型主要是为了科学计算和工程计算而设计的。他们执行二进制浮点运算,这是为了在广泛的数值范围上提供较为精确的快速近似计算而精心设计的。然而,它们并没有提供完全精确的结果,所以不应该被用于需要精确结果的场合。float和double类型尤其不是和用于货币计算,因为要让一个float或者double精确地标识0.1(或者10的任何其他负数次方值)是不能的。
举例说明代码如下:
public static void main(String[] args) { //所有金额 double funds = 1; //购买次数 int itemsBought = 0; //初次购买是0.1,后续每次购买都会涨价0.1 for (double price = 0.1; funds >= price; price += 0.1) { funds -= price; itemsBought++; } System.out.println(String.format("一共能买%d件物品", itemsBought)); System.out.println("余额:" + funds); }
运行结果为:

如上运行的是丢失精度问题。
修改代码如下:
//所有金额 BigDecimal funds = new BigDecimal(1); //购买次数 int itemsBought = 0; //初次购买是0.1,后续每次购买都会涨价0.1 for (BigDecimal price = new BigDecimal("0.1"); funds.compareTo(price) >= 0;price = price.add(new BigDecimal("0.1"))) { funds =funds.subtract(price); itemsBought++; } System.out.println(String.format("一共能买%d件物品", itemsBought)); System.out.println("余额:" + funds);
运行结果为:

Java中的简单浮点数类型float和double不能够精确运算。这个问题其实不是JAVA的bug,因为计算机本身是二进制的,而浮点数实际上只是个近似值,所以从二进制转化为十进制浮点数时,精度容易丢失,导致精度下降。
四、BigDecimal用法
如下:加减乘除用法
/** * 相加 * @param doubleValA * @param doubleValB * @return */ public static double add(String doubleValA, String doubleValB) { BigDecimal a2 = new BigDecimal(doubleValA); BigDecimal b2 = new BigDecimal(doubleValB); return a2.add(b2).doubleValue(); } /** * 相减 * @param doubleValA * @param doubleValB * @return */ public static double sub(String doubleValA, String doubleValB) { BigDecimal a2 = new BigDecimal(doubleValA); BigDecimal b2 = new BigDecimal(doubleValB); return a2.subtract(b2).doubleValue(); } /** * 相乘 * @param doubleValA * @param doubleValB * @return */ public static double mul(String doubleValA, String doubleValB) { BigDecimal a2 = new BigDecimal(doubleValA); BigDecimal b2 = new BigDecimal(doubleValB); return a2.multiply(b2).doubleValue(); } /** * 相除 * @param doubleValA * @param doubleValB * @param scale 除不尽时指定精度 * @return */ public static double div(String doubleValA, String doubleValB, int scale) { BigDecimal a2 = new BigDecimal(doubleValA); BigDecimal b2 = new BigDecimal(doubleValB); return a2.divide(b2, scale, BigDecimal.ROUND_HALF_UP).doubleValue(); }
主函数调用结果:
public static void main(String[] args) { String doubleValA = "3.14159267"; String doubleValB = "2.358"; System.out.println("add:" + add(doubleValA, doubleValB)); System.out.println("sub:" + sub(doubleValA, doubleValB)); System.out.println("mul:" + mul(doubleValA, doubleValB)); System.out.println("div:" + div(doubleValA, doubleValB, 8)); }
运行如下:

总结:
1、对于任何需要精确答案的计算任务,请不要使用float或者double。
2、如果你想让系统来记录十进制小数点,并且不介意因为不使用基本类型而带来的不便,就请使用BigDecimal。使用BigDecimal还有一些额外的好处,他允许你完全控制舍入,每当一个操作涉及舍入的时候,他允许你从8种舍入模式中选择其一。如果你正通过法定要求的舍入行为进行业务计算,使用BigDecimal是非常方便的。
3、如果性能非常关键,并且你不介意自己记录十进制小数点,而且所涉及的数值又不太大,就可以使用int或者long。如果数值范围内没有超过9位十进制数字,就可以使用int;如果不超过18位数字,就可以使用long。如果数值可能超过18位数字,就必须使用BigDecimal。



