李群李代数(第一次会晕)
- 三维旋转矩阵构成特殊正交群,SO(3),变换矩阵构成了特殊欧式群SE(3).
$${\rm{SO(3) = \{ R}} \in {{\rm{R}}^{3 \times 3}}\left| {R{R^T} = I,\det (R) = I} \right.{\rm{\} }}$$
\[{\rm{SE(3) = }}\left\{ {{\rm{T = }}\left[ {\begin{array}{*{20}{c}}
R&t\\
0&1
\end{array}} \right] \in {{\rm{R}}^{4 \times 4}}\left| {R \in SO(3),t \in {R^3}} \right.} \right\}\]
- 从上面看群是一种集合加上一种运算的代数结构。什么集合,何种运算不知道。把集合记作A,运算记作$ \bullet $,群记为$G = (A, \bullet )$,群应满足以下四个特性(封结幺逆):
- 封闭性:$\forall {a_1},{a_2} \in A,\;\;\;\;\;{a_1} \bullet {a_2} \in A$
- 结合律:
\[\forall {a_1},{a_2},{a_3} \in A,\;\;\;\;\;({a_1} \bullet {a_2}) \bullet {a_3} = {a_1} \bullet ({a_2} \bullet {a_3})\]
- 幺元:$\exists {a_0} \in A,s.t\;\forall a \in A,{a_0} \bullet a = a \bullet {a_0} = a$
- 逆:$\forall a \in A,\;\;\;\exists {a^{{\rm{ - }}1}} \in A,s.t\;a \bullet {a^{_{{\rm{ - }}1}}} = a$
- 李群是指具有连续光滑性质的群,像一般的整数离散群不具有连续性,SO(3), SE(3)在实数空间上是连续的,表示一个位置变换到另一个位置,路径是连续的。但是群的概念只定义了乘法,没有加法。
-
李代数的引出:
李代数由一个集合V、一个数域F和一个二元运算[ ,](李括号)组成。称(V,F,[ , ])为一个李代数,记为g.
在实际应用中我们估计相机的位置和姿态时,由于干扰,不可能没有误差,那么产生误差需要矫正,我们会用补偿量$\Delta R,\Delta T$去补偿误差。然而群的定义对加法没有封闭性,比如两个旋转或变换矩阵相加后不再表示一个旋转或变换矩阵,失去了原有的意义,于是李代数的提出为此问题提供了解决思路,把SE(3)空间的T映射为李代数se(3),它由向量组成,我们在中学数学就知道,向量相加还表示为一个向量(例如平行四边形原则),李代数对加法具有封闭性(加完之后还是向量)。这样可以通过李代数求导间接对变换矩阵T进行求导。在优化相机位姿时,每次迭代更新一个位姿的增量δ,使目标函数最小,那么这个δ就是通过对T微分得到的。它们对于某时刻的R(t)(李群空间),存在一个三维向量$\phi {\rm{ = (}}{\phi _1}{\rm{,}}{\phi _2}{\rm{,}}{\phi _3}{\rm{)}}$的李代数空间来描述R在t时刻的导数。
\[\mathop R\limits^ \bullet (t) = \phi {(t)^ \wedge }R(t) = \left[ {\begin{array}{*{20}{c}}
0&{ - {\phi _3}}&{{\phi _2}}\\
{{\phi _3}}&0&{ - {\phi _1}}\\
{ - {\phi _2}}&{{\phi _1}}&0
\end{array}} \right]R(t)\]
- 指数映射:向量$\phi {\rm{ = (}}{\phi _1}{\rm{,}}{\phi _2}{\rm{,}}{\phi _3}{\rm{)}}$反映了R的导数性质,它们之间的微分关系可以描述为:李代数so(3)对应李群SO(3) 在原点附近的正切空间。换句话说,李代数so(3)是三维向量$\phi {\rm{ = (}}{\phi _1}{\rm{,}}{\phi _2}{\rm{,}}{\phi _3}{\rm{)}}$的集合,每个$\phi (i)$的反对称矩阵都$\phi (i)$^可以表示SO(3)上旋转矩阵$R(i)$的导数,R和$\phi $呢又呈现一个指数映射关系:$R(t) = \exp (\phi _0^ \wedge t)$,$\exp ({\phi ^ \wedge }) = \exp (\theta {{\rm{a}}^ \wedge }) = \sum\limits_{n = 0}^\infty {\frac{1}{{n!}}} {(\theta {{\rm{a}}^ \wedge })^n}$经过泰勒展开后变为$\exp (\theta {{\rm{a}}^ \wedge }) = \cos \theta I + (1 - \cos \theta )a{a^T} + \sin \theta {a^ \wedge }$又回到了罗德里格斯。对于三维旋转和变换的关系图如下;
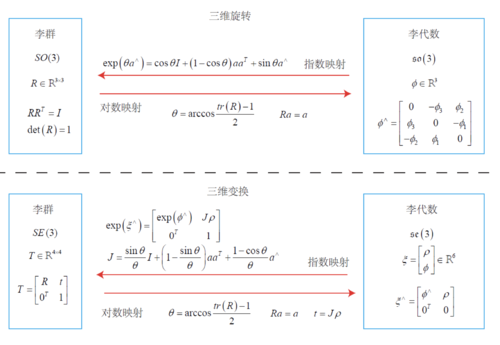
- 李代数求导与扰动模型:
以SO(3)为例,当李代数的so(3)做加法时,在李群SO(3)是否对应为两个矩阵的乘积,$\exp (\phi _1^ \wedge )\exp (\phi _2^ \wedge ) = \exp ({({\phi _1} + {\phi _2})^ \wedge })$?$\ln (\exp (A)\exp (B)) = A{\rm{ + }}B$?答案是对矩阵运算都不成立,BCH公式给出了近似解:
\[\ln {(\exp (A\phi _1^ \wedge )\exp (\phi _2^ \wedge ))^ \vee } \approx \left\{ {\begin{array}{*{20}{c}}
{{J_l}{{({\phi _2})}^{ - 1}}{\phi _1} + {\phi _2},{\phi _1}\min }\\
{{J_r}{{({\phi _1})}^{ - 1}}{\phi _2} + {\phi _1},{\phi _2}\min }
\end{array}} \right.\]
以下标为l的左乘模型来说,意思是,我们对一个旋转矩阵R2 (李代数${\phi _2}$)左乘一个微小旋转矩阵R1 (李代数${\phi _1}$ ),看成是李代数 ${\phi _2}$加上一项
\[{J_l}{({\phi _2})^{ - 1}}{\phi _1}\]
右乘模型同理。式中有一个近似的雅可比Jl,再通俗的形象一下就是,假定对一个旋转R(李代数$\phi $)产生的漂移进行矫正,左乘一个$\Delta R$ (李代数$\Delta \phi $),在李群上的结果为$\Delta R \bullet R$
用BCH近似为
\[{J_l}{(\phi )^{ - 1}}\Delta \phi {\rm{ + }}\phi \]
合起来就是$\exp (\Delta {\phi ^ \wedge })\exp ({\phi ^ \wedge }) = \exp ({(\phi + {J_l}(\phi )\Delta \phi )^ \wedge })$,然而上面刚刚说到在李代数上加法是封闭的,可以进行加法运算,一个
\[\phi {\rm{ + }}\Delta \phi \]
可以近似为李群上带左右雅可比的乘法:$\exp ({(\phi + \Delta \phi )^ \wedge }) = \exp ({({J_l}\Delta \phi )^ \wedge })\exp ({\phi ^ \wedge }) = \exp ({\phi ^ \wedge })\exp ({({J_r}\Delta \phi )^ \wedge })$
- 求导运算1
空间中有一向量p,然后我们对其进行了R的旋转变换变为Rp,求旋转之后Rp对旋转R的导数,$\frac{{\partial (Rp)}}{{\partial R}}$ ,但是没有加法,无法按照导数定义计算,因此转为李代数计算。
$$\frac{{\partial (Rp)}}{{\partial R}}{\rm{ = }}\frac{{\partial (\exp ({\phi ^ \wedge })p)}}{{\partial \phi }} = - {(Rp)^ \wedge }{J_l}$$
结果中有一个雅可比,在应用中不太好处理,又出现了扰动模型来替代,思路是对R进行一次扰动$\Delta R$(左乘形式),看结果相对扰动的变化率。 $\Delta R$对应的李代数为 $\varphi $,$\frac{{\partial (Rp)}}{{\partial \varphi }}{\rm{ = }} - {(Rp)^ \wedge }$,这样就没有了雅可比,对实际应用更加合理。
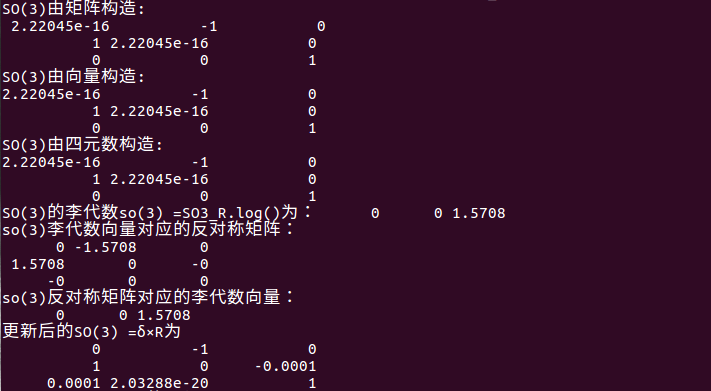
- 实现才是硬道理:
1 #include<iostream> 2 #include<cmath> 3 #include<Eigen/Core> 4 #include<Eigen/Geometry> 5 #include"sophus/se3.h" 6 #include"sophus/so3.h" 7 8 using namespace std; 9 using namespace Eigen; 10 11 int main(int argc,char **argv) 12 { 13 // 沿Z轴转90度的旋转矩阵用旋转向量表示 14 Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix(); 15 16 Sophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接从旋转矩阵构造 17 Sophus::SO3 SO3_v( 0, 0, M_PI/2 ); // 亦可从旋转向量构造 18 Eigen::Quaterniond q(R); // 或者四元数 19 Sophus::SO3 SO3_q( q ); 20 // 上述表达方式都是等价的 21 22 cout<<"SO(3)由矩阵构造:\n "<<SO3_R.matrix()<<endl; 23 cout<<"SO(3)由向量构造: \n"<<SO3_v.matrix()<<endl; 24 cout<<"SO(3)由四元数构造:\n"<<SO3_q.matrix()<<endl; 25 26 // 使用对数映射获得它的李代数 27 Eigen::Vector3d so3 = SO3_R.log(); 28 cout<<"SO(3)的李代数so(3) =SO3_R.log()为: "<<so3.transpose()<<endl; 29 // hat 为向量到反对称矩阵 30 cout<<"so(3)李代数向量对应的反对称矩阵: \n"<<Sophus::SO3::hat(so3)<<endl; 31 // 相对的,vee为反对称矩阵到向量 32 cout<<"so(3)反对称矩阵对应的李代数向量: \n "<<Sophus::SO3::vee( Sophus::SO3::hat(so3) ).transpose()<<endl; 33 // transpose纯粹是为了输出美观一些 34 35 // 增量扰动模型的更新 36 Eigen::Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多 37 Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3)*SO3_R; 38 cout<<"更新后的SO(3) =δ×R为 \n"<<SO3_updated.matrix()<<endl; 39 40 cout<<"***********SE(3)的操作*************"<<endl; 41 // 对SE(3)操作大同小异 42 Eigen::Vector3d t(1,0,0); // 沿X轴平移1 43 Sophus::SE3 SE3_Rt(R, t); // 从R,t构造SE(3) 44 Sophus::SE3 SE3_qt(q,t); // 从q,t构造SE(3) 45 cout<<"SE3由矩阵旋转+平移构造( R,t)= "<<endl<<SE3_Rt.matrix()<<endl; 46 cout<<"SE3由四元数q,t= "<<endl<<SE3_qt.matrix()<<endl; 47 // 李代数se(3) 是一个六维向量,方便起见先typedef一下 48 typedef Eigen::Matrix<double,6,1> Vector6d; 49 Vector6d se3 = SE3_Rt.log(); 50 cout<<"SE(3)对应的李代数se(3) =\n "<<se3.transpose()<<endl; 51 // 观察输出,会发现在Sophus中,se(3)的平移在前,旋转在后. 52 // 同样的,有hat和vee两个算符 53 cout<<"se(3)对应的反对称矩阵 = "<<endl<<Sophus::SE3::hat(se3)<<endl; 54 cout<<"反对称矩阵对应的李代数向量 = "<<Sophus::SE3::vee( Sophus::SE3::hat(se3) ).transpose()<<endl; 55 56 // se(3)的扰动 57 Vector6d update_se3; //更新量 58 update_se3.setZero();//六维更新量 59 update_se3(0,0) = 1e-4d;//改变其中一个量来产生观测 60 Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3)*SE3_Rt; 61 cout<<"更新后的SE(3) = "<<endl<<SE3_updated.matrix()<<endl; 62 63 return 0; 64 }