旋转矩阵、旋转向量、欧拉角、四元数的关系
- 向量的矩阵形式
有两个向量：
\[\overrightarrow {\rm{a}} = ({a_1},{a_2},{a_3})\]
\[\overrightarrow {\rm{b}} = ({b_1},{b_2},{b_3})\]
叉乘的结果表示一个向量，这个向量向量垂直于a,b向量构成的平面。
\[\overrightarrow a \times \overrightarrow {\rm{b}} = \left\| {\begin{array}{*{20}{c}}
{{e_1}}&{{e_2}}&{{e_3}}\\
{{a_1}}&{{a_2}}&{{a_3}}\\
{{b_1}}&{{b_2}}&{{b_3}}
\end{array}} \right\| = \left[ {\begin{array}{*{20}{c}}
{{a_2}{b_3} - {a_3}{b_2}}\\
{{a_3}{b_1} - {a_1}{b_3}}\\
{{a_1}{b_2} - {a_2}{b_1}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
0&{ - {a_3}}&{{a_2}}\\
{{a_3}}&0&{ - {a_1}}\\
{ - {a_2}}&{{a_1}}&0
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{b_1}}\\
{{b_2}}\\
{{b_3}}
\end{array}} \right] = {a^ \wedge }b\]
将向量a对应的矩阵表示出来，为一个反对称矩阵，每一个向量都对应着一个反对称矩阵。这就引出向量的矩阵形式。
\[{a^ \wedge } = \left[ {\begin{array}{*{20}{c}}
0&{ - {a_3}}&{{a_2}}\\
{{a_3}}&0&{ - {a_1}}\\
{ - {a_2}}&{{a_1}}&0
\end{array}} \right]\]
- 坐标变换的易混点
在齐次变换中
\[{{\rm{p}}_1} = {T_{12}} \bullet {p_2}\]
\[{{\rm{p}}_2} = {T_{23}} \bullet {p_3}\]
T12表示，把坐标系{2}的向量变换到坐标系{1}中，T23同理，如果把坐标系{3}下的向量变换到坐标系{1}中为：
\[{{\rm{p}}_1} = {T_{12}} \bullet {T_{23}} \bullet {p_3}\]
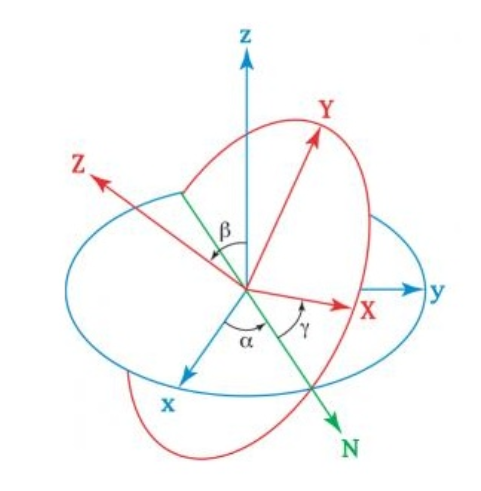
- 旋转向量和欧拉角:
SO(3)的旋转矩阵有9个量，但是只有3个自由度，同理SE(3)有16个量，但是也只有6个自由度。在实际的旋转中，任意的旋转都可用一个旋转轴和一个旋转角来表示，我们使用一个向量，方向与旋转轴一致，长度等于旋转角，这样只需要一个三维向量即可描述旋转。对于SE(3),用一个旋转向量和一个平移向量即可表达，恰好自由度为6.如果用旋转向量来描述R：旋转轴为一个单位长度的向量n,角度为$\theta $，那么$\theta {\rm{n}}$可以表示这个旋转。旋转矩阵R和旋转向量$\theta {\rm{n}}$的转换过程为罗德里格斯变换：
\[R = \cos \theta I + (1 - \cos \theta )n{n^T} + \sin \theta {n^ \wedge }\]
此处末尾的${{\rm{n}}^ \wedge }$ 如上面所示，代表矩阵表示的向量。那么反过来通过旋转矩阵获取转角 $\theta $;
$$\theta {\rm{ = arccos}}\frac{{tr(R) - 1}}{2}$$
tr(R)为矩阵R的迹。对于转轴n,Rn=n;表示为转轴绕自身转动不生改变，从数学来说n是矩阵R特征值为1时对应的特征向量。从现在来看旋转轴和旋转角来表示的旋转是紧凑的，没有冗余性，但是欧拉角RPY的空间中，当一个旋转达到$\underline {\rm{ + }} 90^\circ $是就出现了奇异性。相当于地球的经纬度中当纬度为$\underline {\rm{ + }} 90^\circ $时，经度无意义。
那么如何解决冗余性和奇异性呢，于是又提出了四元数，既不冗余有没有奇异性。
- 四元数
$q = {q_0} + {q_1}i + {q_2}j + {q_3}k$其中i,j,k 为四元数的三个虚部，关系为：
\[\left\{ {\begin{array}{*{20}{c}}
{{i^2}{\rm{ = }}{j^2}{\rm{ = }}{k^2}{\rm{ = }}\; - 1}\\
{ij = k,ji = - k}\\
{jk = i,kj = - i}\\
{ki = j,ik = - j}
\end{array}} \right.\]
i,j,k的关系就像三维坐标系一样，用单位四元数可以表示空间中的任意一个旋转，与复数有一些不同，在复数中，乘以i代表旋转90°，但在四元数中，乘以i对应着旋转180°，保证$ij = k$，对应着绕i旋转180°，在绕j旋转180°等于绕k旋转180°。${i^2} = - 1$意味着绕i轴旋转360°得到一个相反的东西。四元数之间的运算满足上面四个关系。
- 用四元数表示旋转
空间的一个三维点$p = [x,y,z] \in {R^3}$，由一个单位四元数q指定的旋转，三维点$p$经过旋转之后变为$p'$，在原始的矩阵描述为$p' = Rp$，在四元数中描述时:$p = {[0,x,y,z]^T} = {[0,u]^T}$,相当于把四元数的三个虚部与空间中的三个轴对应，旋转后的$p'$可以表示为：$p' = qp{q^{ - 1}}$（不用纠结为什么左乘一个q右乘一个q的逆，运算规则就是这样），结果仍然为四元数。把$p'$的虚部取出得到旋转之后的坐标。
- 说千道万落到实践是关键：
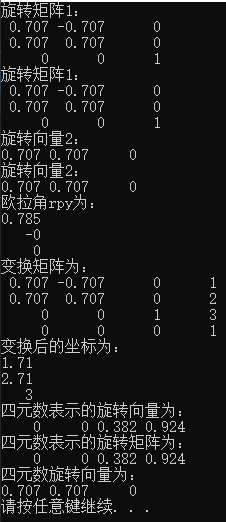
1 Matrix3d R_mat = Matrix3d::Identity();//初始化为单位阵 2 AngleAxisd R_vec(M_PI/4,Vector3d(0,0,1));//用旋转角和旋转轴表示的旋转向量 3 cout.precision(3);//输出精确到三位小数 4 R_mat = R_vec.toRotationMatrix();//旋转向量转化为旋转矩阵 5 cout << "旋转矩阵1：\n"<<R_vec.matrix() << endl //旋转向量转化为旋转矩阵 6 << "旋转矩阵1：\n" << R_mat << endl; 7 8 Vector3d v(1, 0, 0); 9 Vector3d v_r = R_vec * v;//用旋转轴和角表示的坐标变换 10 cout << "旋转向量2：\n" << v_r.transpose() << endl;//transpose()为转置 11 v_r = R_mat * v;//用旋转矩阵表示的坐标变换 12 cout << "旋转向量2：\n" << v_r.transpose() << endl; 13 14 Vector3d eul_ang = R_mat.eulerAngles(2, 1, 0);//ZYX顺序，RPY 15 cout << "欧拉角rpy为：\n" << eul_ang << endl;//绕Z旋转π/4 16 17 Isometry3d T = Isometry3d::Identity();//欧氏变换，4x4矩阵 18 T.rotate(R_vec);//按照R_vec旋转向量来旋转 19 T.pretranslate(Vector3d(1, 2, 3));//平移向量为（1.2.3） 20 cout << "变换矩阵为：\n" <<T.matrix() << endl; 21 22 Vector3d v_transform = T * v;//就是通常的R*v+t,旋转和平移都包括进去了对于坐标第四个数默认补1 23 cout << "变换后的坐标为：\n" << v_transform << endl; 24 25 Quaterniond q = Quaterniond(R_vec);//用四元数表示旋转向量 26 cout << "四元数表示的旋转向量为：\n" << q.coeffs().transpose() << endl;//(i,j,k,w),前三个为虚部，最后一个为实部 27 q = Quaterniond(R_mat);//用四元数表示旋转矩阵 28 cout << "四元数表示的旋转矩阵为：\n" << q.coeffs().transpose() << endl;//(i,j,k,w),前三个为虚部，最后一个为实部 29 30 v_r = q * v;//用四元数表示的旋转变换，数学中是q*v*q.inverse() 31 cout << "四元数旋转向量为：\n" << v_r.transpose() << endl;
