假设检验

假设检验是先对总体参数进行提出某种假设的前提下，利用样本信息判断假设是否成立。

 

假设检验中基本概念

原假设和备择假设

原假设，用H0表示。原假设一般是统计者想要拒绝的假设。

备择假设，用H1表示。备则假设是统计者想要接受的假设。

为什么统计者想要拒绝的假设设置为原假设呢？这是由于若原假设被拒绝如果出错的话，只能犯第I类（弃真）错误，而犯第I类错误的概率已经被规定的显著性水平𝞪所控制。

 

假设检验的两类错误

第Ⅰ类错误（弃真错误）：当原假设为真时拒绝原假设。犯第Ⅰ类错误的概率通常记为α（显著性水平）。

第Ⅱ类错误（纳伪错误）：当原假设为假时接受原假设。犯第Ⅱ类错误的概率通常记为β。

	接受H0	拒绝H0
H0为真	正确决策	第Ⅰ类错误
H0为假	第Ⅱ类错误	正确决策

发生第Ⅰ类错误的概率：如果发生弃真错误，那么一定是拒绝了原假设（样本结果位于拒绝域内），拒绝域由检验水平决定，如果显著性水平为α，则发生弃真错误的概率为α。

 

检验统计量：根据实际情况，用于假设检验计算的统计量，在H0条件下，统计量服从特定的概率分布。

 

拒绝域：若样本观测结果位于拒绝域内，则具有充分理由拒绝H0。若样本观测结果位于拒绝域内，则不拒绝H0。拒绝域取值由显著性水平和统计量分布决定。

 

显著性水平：规定的小概率α，由于小概率事件在一次试验中很难发生，所以若小概率事件发生了，即p值小于α、样本观测值位于拒绝域内，则具有充分理由拒绝H0。

 

p值：样本观测值在拒绝域方向的概率，利用样本进行计算，判定p值是否小于显著性水平即样本结果是否在拒绝域内。

 

检验形式

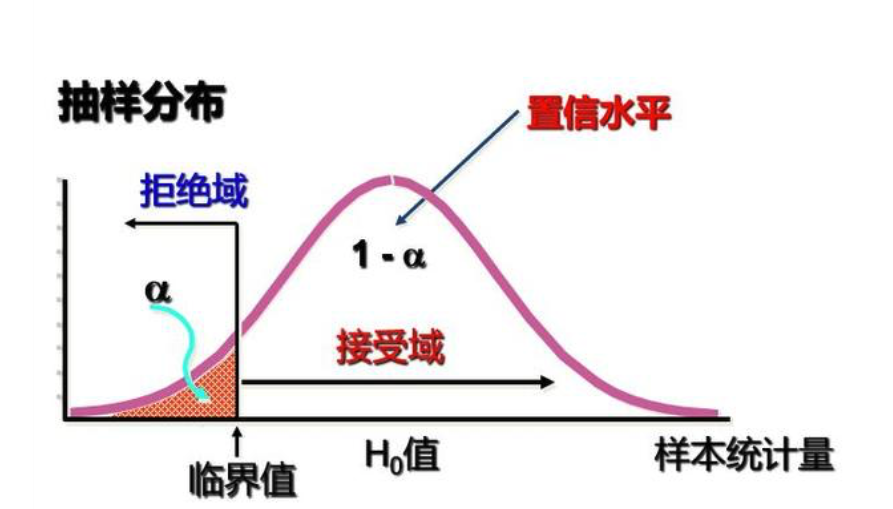
（1）单侧检验

通过备择假设确定左右侧，若备择假设为<，则使用左侧，若备择假设为>，则使用右侧。

 

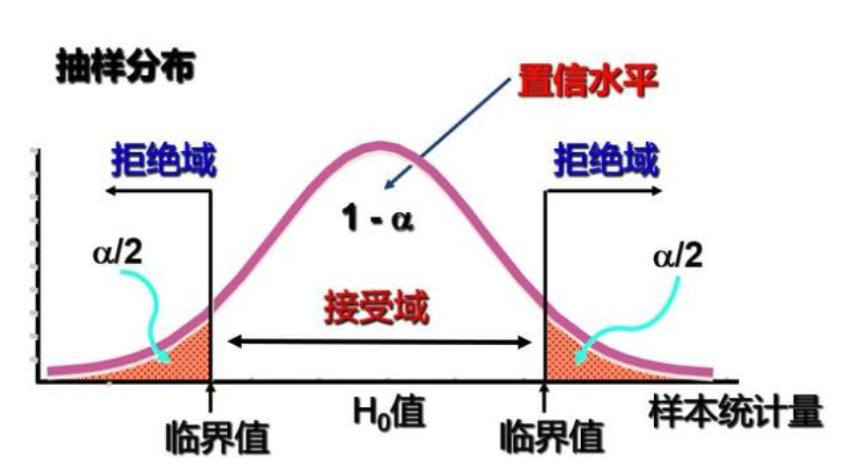
（2）双侧检验

拒绝域一分为二位于数据集的两侧，选择显著性水平，将拒绝域一分为二，两侧概率各占α/2。

若备择假设包含不等号≠，需要使用双侧检验。

 

 

 

假设检验步骤

• 确定要进行检验的假设H0 H1
• 选择检验统计量
• 通过显著性水平确定拒绝域
• 求出检验统计量p值
• 查看样本结果是否位于拒绝域内
• 作出决策

 

例题：

制药厂宣传某药品治愈率能达到90%，医生随机抽取了100位病人，只有80人检测被治愈，还有20位病人未被治愈，我们通过假设检验来看下制药厂的说明是否值得信任。

 

1. 确定假设

H0：p = 0.9

H1：p < 0.9

 

2. 选择统计量

检验统计量表示样本中治愈人数，在H0的条件下，服从二项分布 ~B（100，0.9），二项分布中np、nq均大于5，可用正态分布替代二项分布。

则新检验统计量 服从正态分布 ~N（np，npq）~N（90，9），标准化正态分布可得新检验统计量 。

 

3. 拒绝域

通过备择假设确定检验形式，本题中由于p < 0.9，所以拒绝域位于左侧，在我们已知检验统计量后，利用显著性水平计算拒绝域。

α = 5% ,所以p(Z < c)  = 0.05 ,通过查表可得c = -1.64，c代表拒绝域临界点，拒绝域位于临界点左侧，只要样本检验统计量小于c，则有充分理由拒绝H0。

 

4. 求p值

p值是样本观测值在拒绝域方向的概率。

题目中 治愈人数 = 80，则标准分为 -3.33。

p值计算 = p（Z < -3.33） = 0.0004

 

5. 查看检验统计量是否位于拒绝域内

方法1. p值0.0004小于显著性水平0.05

方法2. 样本观测值-3.33位于临界点左侧（拒绝域内）

 

6. 做出决策

在显著性水平为5%的情况下，有充分利用拒绝原假设。

 

 

2020-05-15 15：43