连续性概率分布-正态分布
一、概率密度函数
概率密度函数用于描述连续随机变量的概率分布,离散型分布中我们通常关注随机变量X取特定值时的概率,在连续型分布中关注X在某数值范围内对应概率。
连续随机变量的概率通过概率密度函数面积表示。对于任何概率分布来说,总概率必须等于1,因此面积必须等于1。
二、正态分布-连续数据的“理想”模型
1. 定义
正态分布通常参数均值𝓊和方差𝜎2 进行定义。𝓊指出分布的中央位置,𝜎指出分散性。
如果一个连续随机变量X符合均值为𝓊、标准差为𝜎的正态分布,通常写作:
![]()
2. 性质

正态分布具有钟型曲线,曲线对称,中间部位的概率密度最大。越是偏离均值,概率密度减小,𝜎越大,正态分布曲线越扁平、越宽。
无论图形怎样,概率密度永远不等于0。
3. 标准正态分布 Z~N(0,1)
标准正态分布是符合均值为0,标准差为1的正态分布。
当需要计算正态分布对应概率的时,计算曲线下面积太过复杂,因此需要将正态分布转化为标准正态分布,通过概率表查找概率。
若X~N(𝓊,𝜎2)
通过标准分变换
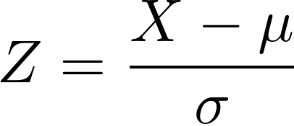
则 Z~N(0,1)。
通过在概率表中查找标准分可求出正态概率,概率表给出的是小于等于这个数值的概率。
三、正态分布应用
1. 线性变换
正态分布的线性变换跟离散变量线性变换一致。
E(aX+b) = aE(X)+b Var(aX+b) = a2Var(X)
若X符合正态分布 X~N(𝓊,𝜎2) ,线性变换aX+b也属于正态分布。
E(X) = 𝓊 ,E(aX+b) = a𝓊+b
Var(X) = 𝜎2 ,Var(aX+b) = a2𝜎2
所以:aX+b ~ N(a𝓊+b,a2𝜎2 )
2. 独立观察值(可看作概率分布完全相同的独立随机变量)
在离散随机变量中,对于独立观察值:
E(X1 + X2 + ... +Xn) = nE(X) Var(X1 + X2 + ... +Xn) = nVar(X)
同样,相同算法适用于连续随机变量,即,如果X符合正态分布 X~N(𝓊,𝜎2)
X1 + X2 + ... +Xn ~ N(n𝓊 ,n𝜎2)。
3. 使用正态分布近似替代二项分布
在离散分布中,我们常用泊松分布近似替代二项分布,以简便计算,当二项分布期望近似等于方差时,即 当q近似等于1且n很大时,np 近似等于npq,泊松分布可近似等于二项分布。
但在某些情况下,我们需要计算某个范围内的概率,这时常用正态分布近似替代二项分布。
通常若二项分布中np和nq双双大于5时,二项分布与正态分布相似。

所以,如果X ~ B(n,p),且np>5,nq>5,则可以使用X ~ N(np,npq)近似代替二项分布。
注意:由于二项分布是离散分布,正态分布则是连续分布,在使用正态分布代替二项分布计算概率时,需要进行连续性修正,确保得到正确的结果。
4. 使用正态分布近似代替泊松分布
当X ~ Po(𝜆) ,随着𝜆变大,泊松分布越来越接近正态分布,即可使用正态分布近似代替泊松分布。
当𝜆大于15时。即若X ~ Po(𝜆)且𝜆>15,我们就能使用X ~ N(𝜆,𝜆) 近似计算 X ~ Po(𝜆)。
同样,为保证结果准确,在正态分布中,需要进行连续性修正。
2020-05-06 17:36



