离散型概率分布-几何分布、二项分布and泊松分布
一、几何分布 X ~ Geo(p)
1. 定义
- 进行一系列相互独立的试验。
- 每次试验都有成功的可能，也有失败的可能，且每次试验成功概率相同。
- 问题在于第一次成功需要进行多少次试验。
2. 概率
随机变量X表示为取得第一次成功所需要的试验次数。
为求出X取特定数值r的概率，使用下式进行计算，
其中p为成功概率，q = 1-p为失败概率。
3. 几何分布的期望和方差
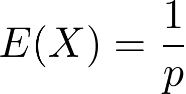
二、二项分布 X ~ B(n,p)
1. 定义
- 进行一系列相互独立的试验，且试验次数有限。
- 每次试验都有成功的可能，也有失败的可能，且每次试验成功概率相同。
- 问题在于n次试验中成功的试验次数。
2. 概率
用X表示“n次试验中的成功次数”，为求出取得r次成功的概率，使用以下公式
其中，p为成功概率，q = 1-p为失败概率，n为试验次数。
3. 二项分布的期望和方差
4. 几何分布和二项分布的同异之处。
相同点：都进行一系列相互独立的实验，且每次试验都会成功和失败两种可能。
不同点：二项分布中规定试验次数n，且在几何分布中关注的点在于“取得第一次成功所需的试验数”，二项分布关注的点在于“n次试验中成功的试验次数”。
三、泊松分布 X~Po(lambda)
1. 定义
已知在一个区间（时间 or 空间）内某事件平均发生次数lambda，问题在于给定区间内的事件发生次数。
2. 概率
在求给定区间内发生r次事件的概率时，使用以下公式。
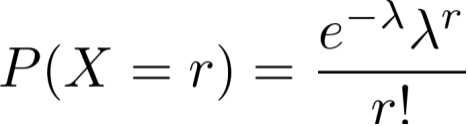，其中lambda为条件里区间内平均发生次数。
3. 泊松分布的期望的方差
4. 使用泊松分布替代二项分布
由于泊松分布中 E(X) = Var(X) = lambda ,二项分布中 E(X) = np ，Var(X) = npq。
所以当二项分布期望近似等于方差时，即 当q近似等于1且n很大时，np 近似等于npq，泊松分布可近似等于二项分布。
典型情况：n>=50 且 p<=0.1。
使用泊松分布替代二项分布是由于考虑到，二项分布计算概率时较为复杂，所以使用泊松分布近似替代二项分布，泊松分布中 lambda = np，即X~Po(np)。
2020-05-03 22:30
