关于堆排序和topK算法的PHP实现
问题描述
topK算法,简而言之,就是求n个数据里的前m大个数据,一般而言,m<<n,也就是说,n可能有几千万,而m只是10或者20这样的两位数。
思路
最简单的思路,当然是使用要先对这n个数据进行排序,因为只有排序以后,才能按照顺序来找出排在前面的,或者排在后面的数据。
假如说我们用快拍,那么时间复杂度是O(nlogn),但是仔细看题目,会发现实际上不要要将所有的数据就进行排序,因为我们找的是前m个数据,所以对所有数据排序实际上有些浪费了。所以可以想到,只维护一个大小为m的数组,然后扫一遍原来的数组n,只将大于数组m里的最小值的数据插入到m数组里,并且重新调整m数组的顺序。
如果使用朴素的方法对m数组进行调整,那么时间复杂度将会是O(n*m),这显然不是最优的结果。对于维护的数组m,我们可以通过维护一个堆结构,来达到每次排序O(logm)的时间复杂度,这样topK算法,总体的复杂度也就变成了O(nlogm)。
关于堆
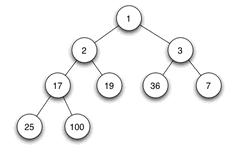
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
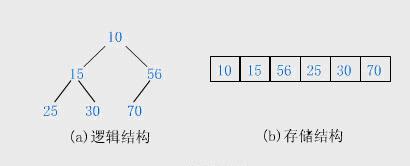
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:一般都用数组来表示堆,i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。
PHP实现的堆
1 class Heap { 2 3 4 5 protected $listSize; 6 7 protected $tree; 8 9 10 11 public function __construct($list) { 12 13 $this->listSize = count($list); 14 15 $i = 1; 16 17 foreach ($list as $li) { 18 19 $this->tree[$i++] = $li; 20 21 } 22 23 unset($list); 24 25 $this->initHeap(); 26 27 } 28 29 30 31 public function getSortedResult() { 32 33 $this->initHeap(); 34 35 $this->sortHeap(); 36 37 return $this->tree; 38 39 } 40 41 42 43 public function getHeapResult() { 44 45 return $this->tree; 46 47 } 48 49 50 51 public function getTopNode() { 52 53 return $this->tree[1]; 54 55 } 56 57 58 59 public function setTopNode($value) { 60 61 $this->tree[1] = $value; 62 63 $this->adjustHeap(1, $this->listSize); 64 65 } 66 67 68 69 public function sortHeap() { 70 71 for ($end = $this->listSize; $end > 1; $end--) { 72 73 $this->swap($this->tree[1], $this->tree[$end]); 74 75 $this->adjustHeap(1, $end - 1); 76 77 } 78 79 } 80 81 82 83 private function initHeap() { 84 85 for ($start=floor($len / 2); $start >= 1; $start--) { 86 87 $this->adjustHeap($start, $this->listSize); 88 89 } 90 91 } 92 93 94 95 private function adjustHeap($start, $len) { 96 97 $tmp = $start; // 临时变量,用于保存最大值或者最小值的下标索引 98 99 $lChildInx = $start * 2; 100 101 $rChildInx = $lChildInx + 1; 102 103 if ($start <= floor($len / 2)) { 104 105 if($lChildInx <= $len && $this->tree[$lChildInx] < $this->tree[$tmp]) { 106 107 $tmp = $lChildInx; 108 109 } 110 111 if($rChildInx <= $len && $this->tree[$rChildInx] < $this->tree[$tmp]) { 112 113 $tmp = $rChildInx; 114 115 } 116 117 if ($tmp != $start) { 118 119 $this->swap($this->tree[$tmp], $this->tree[$start]); 120 121 $this->adjustHeap($tmp, $len); 122 123 } 124 125 } 126 127 } 128 129 130 131 private function swap(&$a, &$b) { 132 133 $temp = $a; 134 135 $a = $b; 136 137 $b = $temp; 138 139 } 140 141 142 143 }
topK
1 include 'Heap.class.php'; 2 3 4 5 $list = range(1,10000); 6 7 shuffle($list); 8 9 $k = 15; 10 11 12 13 $initHeapNodes = array_slice($list, 0, $k); 14 15 $heap = new Heap($initHeapNodes); 16 17 18 19 $n = count($list); 20 21 22 23 for ($i=$k; $i<$n; $i++) { 24 25 if ($list[$i] > $heap->getTopNode()) { 26 27 $heap->setTopNode($list[$i]); 28 29 } 30 31 } 32 33 34 35 print_r($heap->getSortedResult());


