几何概率问题-相遇概率

 假设小白与小仙晚上7点到8点之间都会前往某地看灯展，约定到的人等另外一个人15分钟方可离开，若他们在限时内到达，相遇的概率是多少？

解析：

　　这是一个几何概率问题。他们能见面的充要条件是时间差不超过15分钟，即1/4小时。

　　因为两人没有确切的时间，故样本点由两个数（甲乙两人各自到达的时刻）组成。以7点钟作为原点计算时间的起点，每一分钟为单位画一个正方形60 * 60。落在正方形内的每个点都是一个可能的试验结果。

　　设甲乙各在第x分钟和第y分钟到达，则样本空间为：　　Ω:{(x,y) | 0≤x≤60,0≤y≤60},
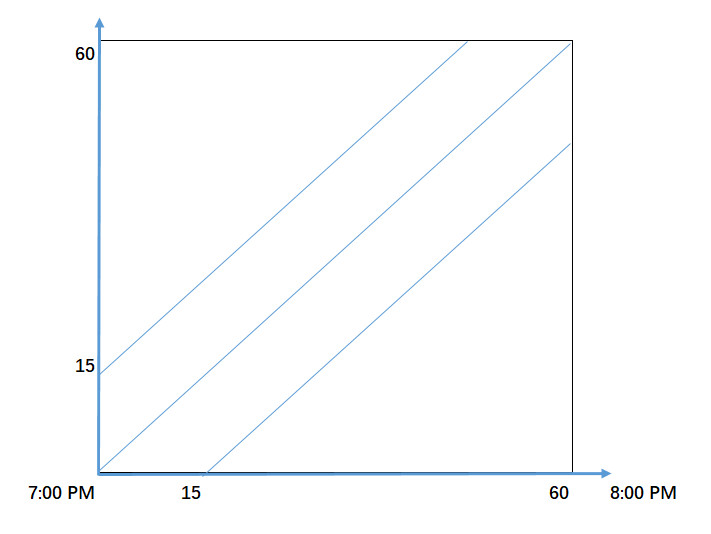
　　画成图为一正方形．会面的充要条件是|x－y| ≤15，即事件A={可以相遇} 所对应的区域是图中的线包围的多边形部分g。

　　P(A)=g的面积/Ω的面积=（60²- (60-15)²）/ 60² 

               = (3600 - 2025) / 3600 = 1575 / 3600 = 0.4375