面试必会的算法题——前缀和
- 作者: 负雪明烛
- id: fuxuemingzhu
- 公众号: 负雪明烛
大家好,我是负雪明烛。
「金九银十」秋招季开始了,相信很多同学已经在投简历、面试了。
算法题是面试的必考点,如何在最短时间内,掌握最多最实用的算法知识呢?我正在本公众号写系列文章:《秋招必会的算法题》,这个系列努力用最通俗易懂的语言,讲解秋招最常见的、必会的算法知识,让大家的时间能获得最大的投资回报率。
欢迎关注「负雪明烛」(CSDN,公众号)。
今天讲的知识是「前缀和」,这是面试常考、又非常容易掌握的算法题技巧。你只用花 15 分钟看完本文就能学会,然后就能秒杀秋招面试遇到的「前缀和」题目。
从「一维数组的动态和」说起
前缀和,英文是 preSum,名字很可怕,但它却是个窗户纸,一捅就破。
为了了解背景,咱们先看 LeetCode 上一个简单题目:1480. 一维数组的动态和。
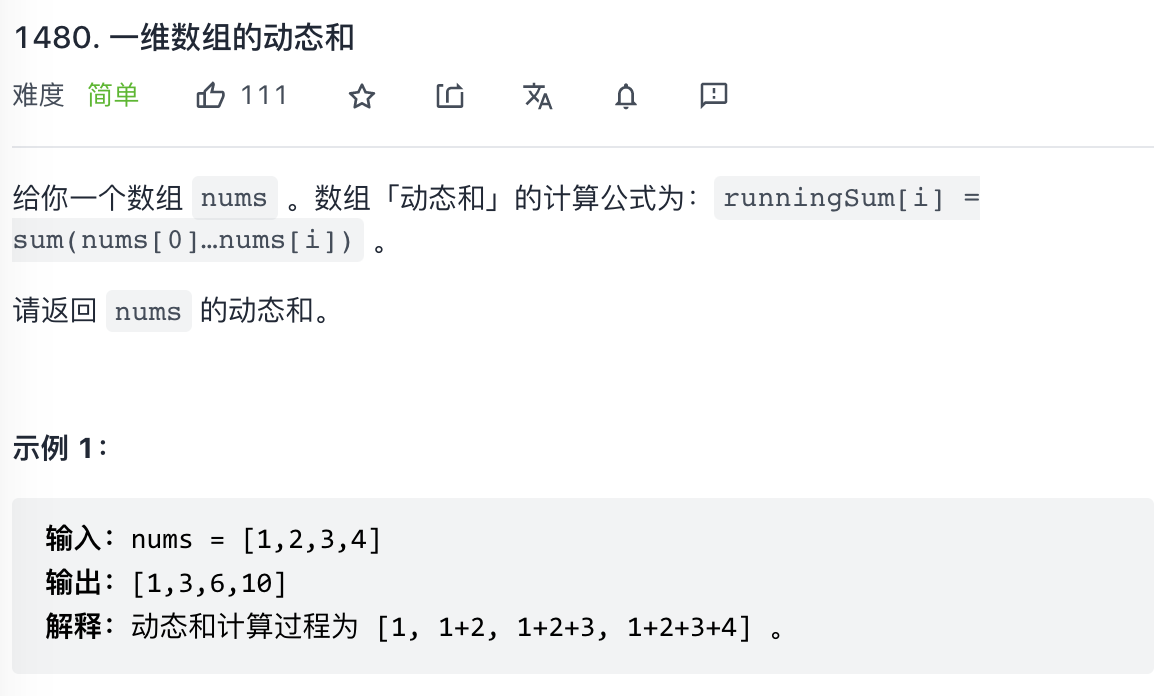
这个题让我们求 runningSum[i] = sum(nums[0]…nums[i]),如果你没有了解过「前缀和」,可能会写出两重循环:每个 runningSum[i],累加从
0
0
0 位置到
i
i
i 位置的 nums[i]。即,写出下面的代码:
vector<int> runningSum(vector<int>& nums) {
const int N = nums.size();
vector<int> preSum(N, 0);
for (int i = 0; i < N; ++i) {
int sum = 0;
for (int j = 0; j <= i; ++j) {
sum += nums[j];
}
preSum[i] = sum;
}
return preSum;
}
两重循环的时间复杂度是
O
(
N
2
)
O(N^2)
O(N2),效率比较低。
其实我们只要稍微转变一下思路,就发现没必要用两重循环。
当已经求出 runningSum[i] = sum(nums[0]…nums[i]),
那么 runningSum[i + 1] = sum(nums[0]…nums[i]) + nums[i + 1]
= runningSum[i] + nums[i + 1]。
就是这个简单的转换,让我们可以省去内层的循环。写出的代码如下:
vector<int> runningSum(vector<int>& nums) {
const int N = nums.size();
vector<int> preSum(N, 0);
for (int i = 0; i < N; ++i) {
if (i == 0) {
preSum[i] = nums[i];
} else {
preSum[i] = preSum[i - 1] + nums[i];
}
}
return preSum;
}
「前缀和」是什么
如果理解了上面的内容,那么我告诉你,preSum 数组其实就是「前缀和」!就是这么简单!
「前缀和」 是从 nums 数组中的第 0 位置开始累加,到第
i
i
i 位置的累加结果,我们常把这个结果保存到数组 preSum 中,记为 preSum[i]。
在前面计算「前缀和」的代码中,计算公式为 preSum[i] = preSum[i - 1] + nums[i] ,为了防止当 i = 0 的时候数组越界,所以加了个 if (i == 0) 的判断,即 i == 0 时让 preSum[i] = nums[i]。
在其他常见的写法中,为了省去这个 if 判断,我们常常把「前缀和」数组 preSum 的长度定义为 原数组的长度 + 1。preSum 的第 0 个位置,相当于一个占位符,置为 0。
那么就可以把 preSum 的公式统一为 preSum[i] = preSum[i - 1] + nums[i - 1],此时的preSum[i]表示nums中
i
i
i 元素左边所有元素之和(不包含当前元素
i
i
i)。
下面以 [1, 12, -5, -6, 50, 3] 为例,用动图讲解一下如何求 preSum。
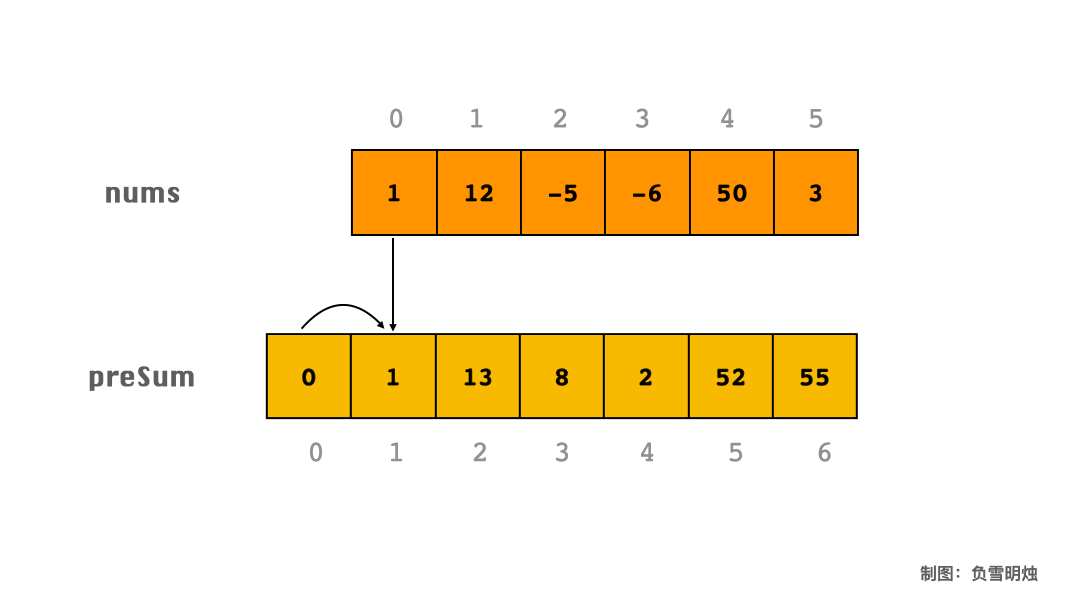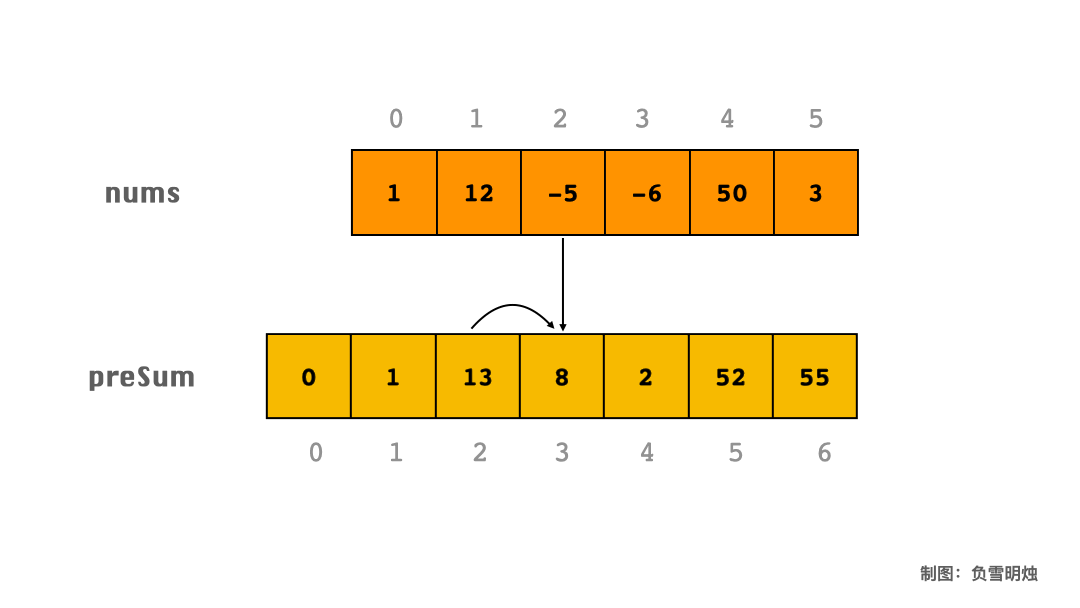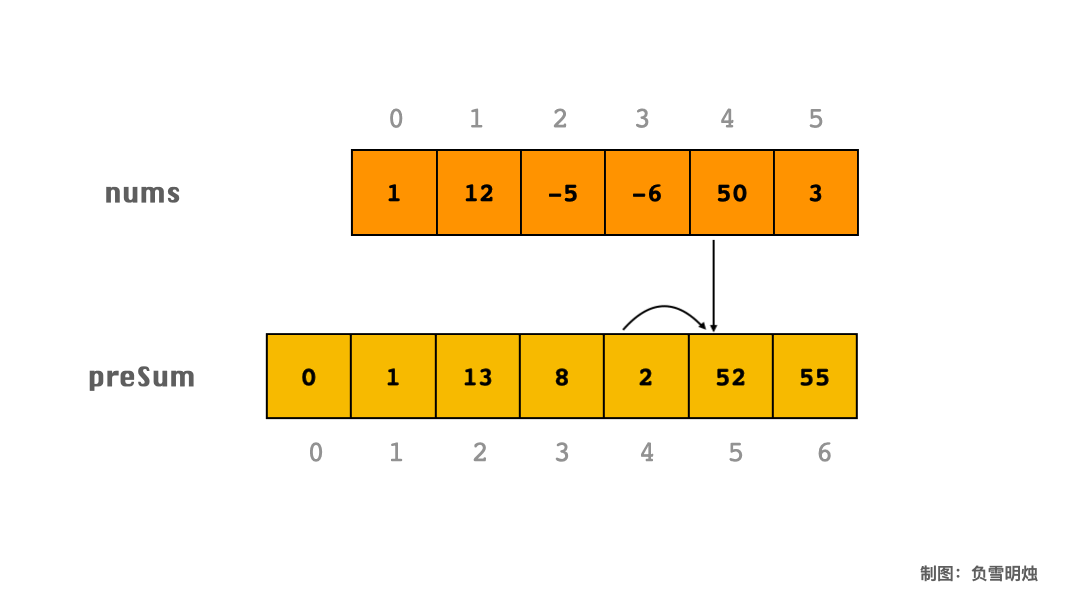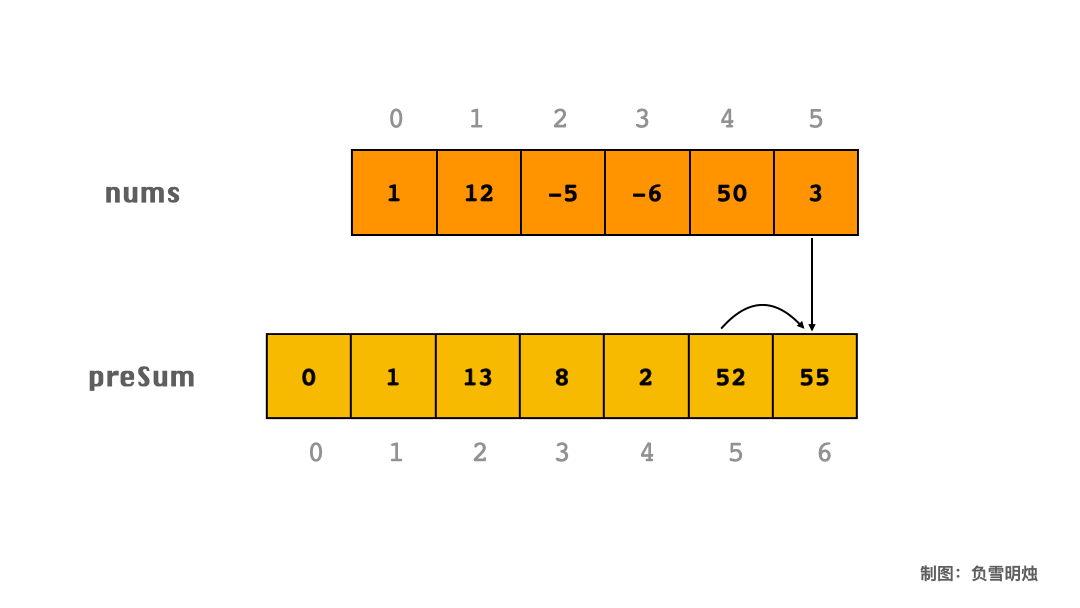
上图表示:
preSum[0] = 0;
preSum[1] = preSum[0] + nums[0];
preSum[2] = preSum[1] + nums[1];
...
「前缀和」有什么用
用途一:求数组前 i i i 个数之和
求数组前
i
i
i 个数之和,是「前缀和」数组的定义,所以是最基本的用法。
举例而言:
- 如果要求
nums数组中的前 2 个数的和(即 s u m ( n u m s [ 0 ] , n u m s [ 1 ] ) sum(nums[0], nums[1]) sum(nums[0],nums[1]) ),直接返回 p r e S u m [ 2 ] preSum[2] preSum[2] 即可。 - 同理,如果要求
nums数组中所有元素的和(即 s u m ( n u m s [ 0 ] . . n u m s [ l e n g t h − 1 ] ) sum(nums[0]..nums[length - 1]) sum(nums[0]..nums[length−1])),直接返回 p r e S u m [ l e n g t h ] preSum[length] preSum[length] 即可。
用途二:求数组的区间和
利用 preSum 数组,可以在
O
(
1
)
O(1)
O(1) 的时间内快速求出 nums 任意区间
[
i
,
j
]
[i, j]
[i,j] (两端都包含) 内的所有元素之和。
公式为: s u m ( i , j ) = p r e S u m [ j + 1 ] − p r e S u m [ i ] sum(i, j) = preSum[j + 1] - preSum[i] sum(i,j)=preSum[j+1]−preSum[i]
什么原理呢?其实就是消除公共部分即 0~i-1 部分的和,那么就能得到 i~j 部分的区间和。
注意上面的式子中,使用的是 preSum[j + 1] 和 preSum[i],需要理解为什么这么做。(如果理解不了的知识,那就记不住,所以一定要理解)
preSum[j + 1]表示的是nums数组中 [ 0 , j ] [0, j] [0,j] 的所有数字之和(包含 0 0 0 和 j j j)。preSum[i]表示的是nums数组中 [ 0 , i − 1 ] [0, i - 1] [0,i−1] 的所有数字之和(包含 0 0 0 和 i − 1 i - 1 i−1)。- 当两者相减时,结果留下了
nums数组中 [ i , j ] [i, j] [i,j] 的所有数字之和。
「前缀和」例题
在了解「前缀和」是什么、有什么用之后,咱们练习一个简单的例题。这个题是 303. 区域和检索 - 数组不可变。题意是给出了一个整数数组 nums,当调用 sumRange(i, j)函数的时候,求数组 nums 中
i
i
i 到
j
j
j 的所有元素总和(包含
i
i
i 和
j
j
j)。

看到这里,相信大家已经都知道了,直接使用「前缀和」不就秒杀了嘛!
下面,我贴一下三种语言的代码。
- Python
class NumArray:
def __init__(self, nums: List[int]):
N = len(nums)
self.preSum = [0] * (N + 1)
for i in range(N):
self.preSum[i + 1] = self.preSum[i] + nums[i]
def sumRange(self, i: int, j: int) -> int:
return self.preSum[j + 1] - self.preSum[i]
- C++
class NumArray {
public:
NumArray(vector<int>& nums) {
const int N = nums.size();
preSum.resize(N + 1);
for (int i = 0; i < N; ++i) {
preSum[i + 1] = preSum[i] + nums[i];
}
}
int sumRange(int i, int j) {
return preSum[j + 1] - preSum[i];
}
private:
vector<int> preSum;
};
- Java
class NumArray {
private int[] preSum;
public NumArray(int[] nums) {
final int N = nums.length;
preSum = new int[N + 1];
for (int i = 0; i < N; ++i) {
preSum[i + 1] = preSum[i] + nums[i];
}
}
public int sumRange(int i, int j) {
return preSum[j + 1] - preSum[i];
}
}
复杂度分析
- 空间复杂度:定义「前缀和」数组,需要 N + 1 N + 1 N+1 的空间,所以空间复杂度是 O ( N ) O(N) O(N);
- 时间复杂度:
- 初始化「前缀和」数组,需要把数组遍历一次,时间复杂度是 O ( N ) O(N) O(N);
- 求
i
j
i ~ j
i j 范围内的区间和,只用访问
preSum[j + 1]和preSum[i],时间复杂度是 O ( 1 ) O(1) O(1)。
拓展
拓展一:隐藏的「前缀和」
算法题目就像一棵大树长出的很多树叶,虽然每片叶子长得都不同,但是它们都有共同的一个主干。算法题的知识点是有限的,有大量的题目都是同一个解法批了不同的皮。
我们以 643. 子数组最大平均数 I 为例,这个题目要求数组 nums 中所有长度为 k 的连续子数组中的最大的平均数。
这个题可以用「前缀和」来解决,也可以用固定大小为 k 的「滑动窗口」来解决。
要求大小为 k 的窗口内的最大平均数,可以求
[
i
,
i
+
k
]
[i, i + k]
[i,i+k] 区间的最大「和」再除以 k,即要求 (preSum[i + k] - preSum[i]) / k 的最大值。
总之,如果题目要求「区间和」的时候,那么就可以考虑使用「前缀和」。
拓展二:二维矩阵的「前缀和」
另外一种拓展,是求二维矩阵的「前缀和」。比如第 304. 二维区域和检索 - 矩阵不可变。
当「前缀和」拓展到二维区间时,可以用下面的思路求解。
步骤一:求 preSum
我们定义 preSum[i][j] 表示 从 [0,0] 位置到 [i,j] 位置的子矩形所有元素之和。
如果求 preSum[i][j] 的递推公式为:
p
r
e
S
u
m
[
i
]
[
j
]
=
p
r
e
S
u
m
[
i
−
1
]
[
j
]
+
p
r
e
S
u
m
[
i
]
[
j
−
1
]
−
p
r
e
S
u
m
[
i
−
1
]
[
j
−
1
]
+
m
a
t
r
i
x
[
i
]
[
j
]
preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i][j]
preSum[i][j]=preSum[i−1][j]+preSum[i][j−1]−preSum[i−1][j−1]+matrix[i][j]
可以用下图帮助理解:
S
(
O
,
D
)
=
S
(
O
,
C
)
+
S
(
O
,
B
)
−
S
(
O
,
A
)
+
D
S(O, D) = S(O, C) + S(O, B) - S(O, A) + D
S(O,D)=S(O,C)+S(O,B)−S(O,A)+D
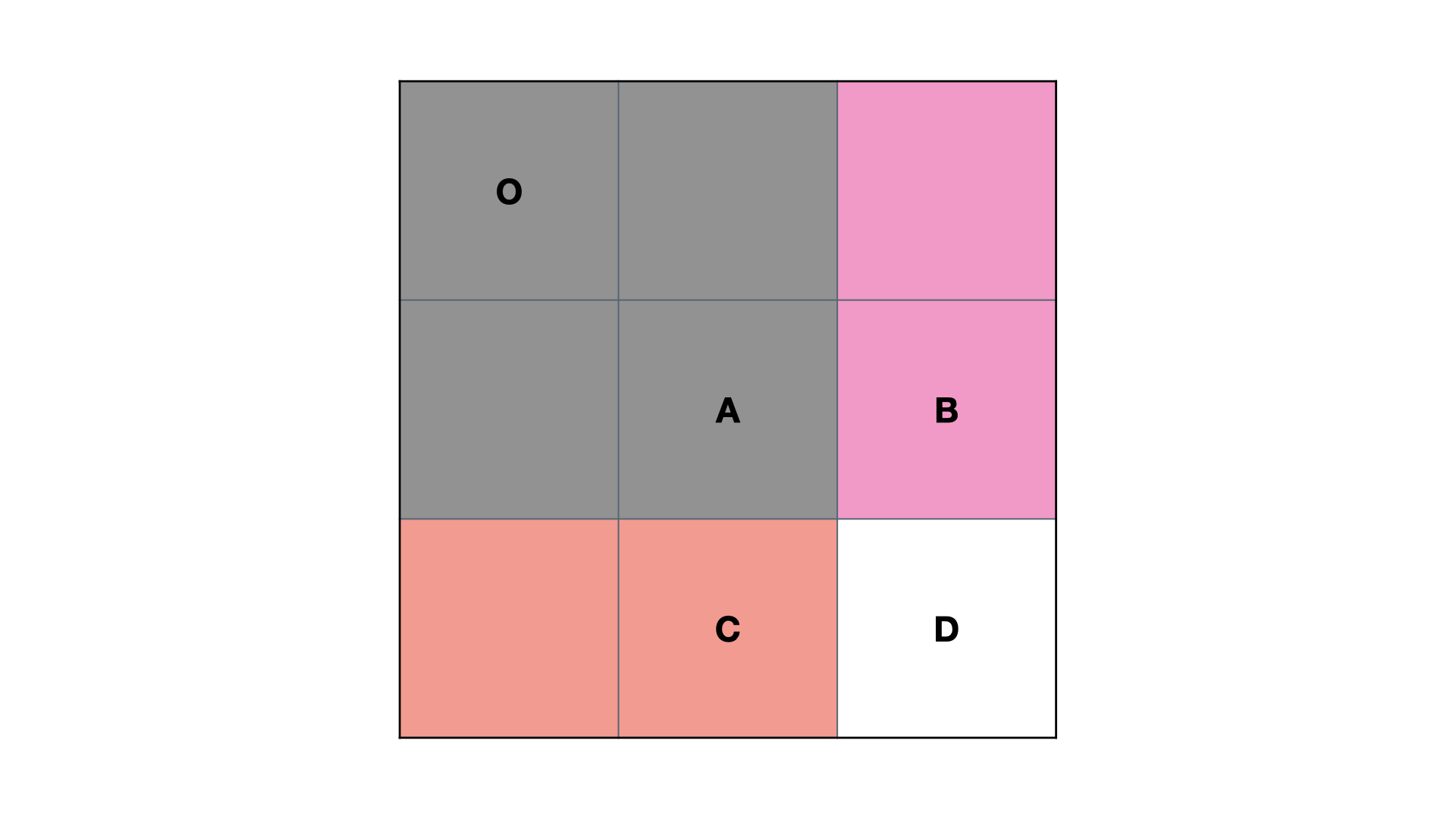
减去 S ( O , A ) S(O, A) S(O,A) 的原因是 S ( O , C ) S(O, C) S(O,C) 和 S ( O , B ) S(O, B) S(O,B) 中都有 S ( O , A ) S(O, A) S(O,A),即加了两次 S ( O , A ) S(O, A) S(O,A),所以需要减去一次 S ( O , A ) S(O, A) S(O,A)。
步骤二:根据 preSum 求子矩形面积
前面已经求出了数组中从 [0,0] 位置到 [i,j] 位置的 preSum。
如果要求 [row1, col1] 到 [row2, col2] 的子矩形的面积的话,用 preSum 计算时对应了以下的递推公式:
p
r
e
S
u
m
[
r
o
w
2
]
[
c
o
l
2
]
−
p
r
e
S
u
m
[
r
o
w
2
]
[
c
o
l
1
−
1
]
−
p
r
e
S
u
m
[
r
o
w
1
−
1
]
[
c
o
l
2
]
+
p
r
e
S
u
m
[
r
o
w
1
−
1
]
[
c
o
l
1
−
1
]
preSum[row2][col2] - preSum[row2][col1 - 1] - preSum[row1 - 1][col2] + preSum[row1 - 1][col1 - 1]
preSum[row2][col2]−preSum[row2][col1−1]−preSum[row1−1][col2]+preSum[row1−1][col1−1]
同样利用一张图来说明:
S
(
A
,
D
)
=
S
(
O
,
D
)
−
S
(
O
,
E
)
−
S
(
O
,
F
)
+
S
(
O
,
G
)
S(A, D) = S(O, D) - S(O, E) - S(O, F) + S(O, G)
S(A,D)=S(O,D)−S(O,E)−S(O,F)+S(O,G)
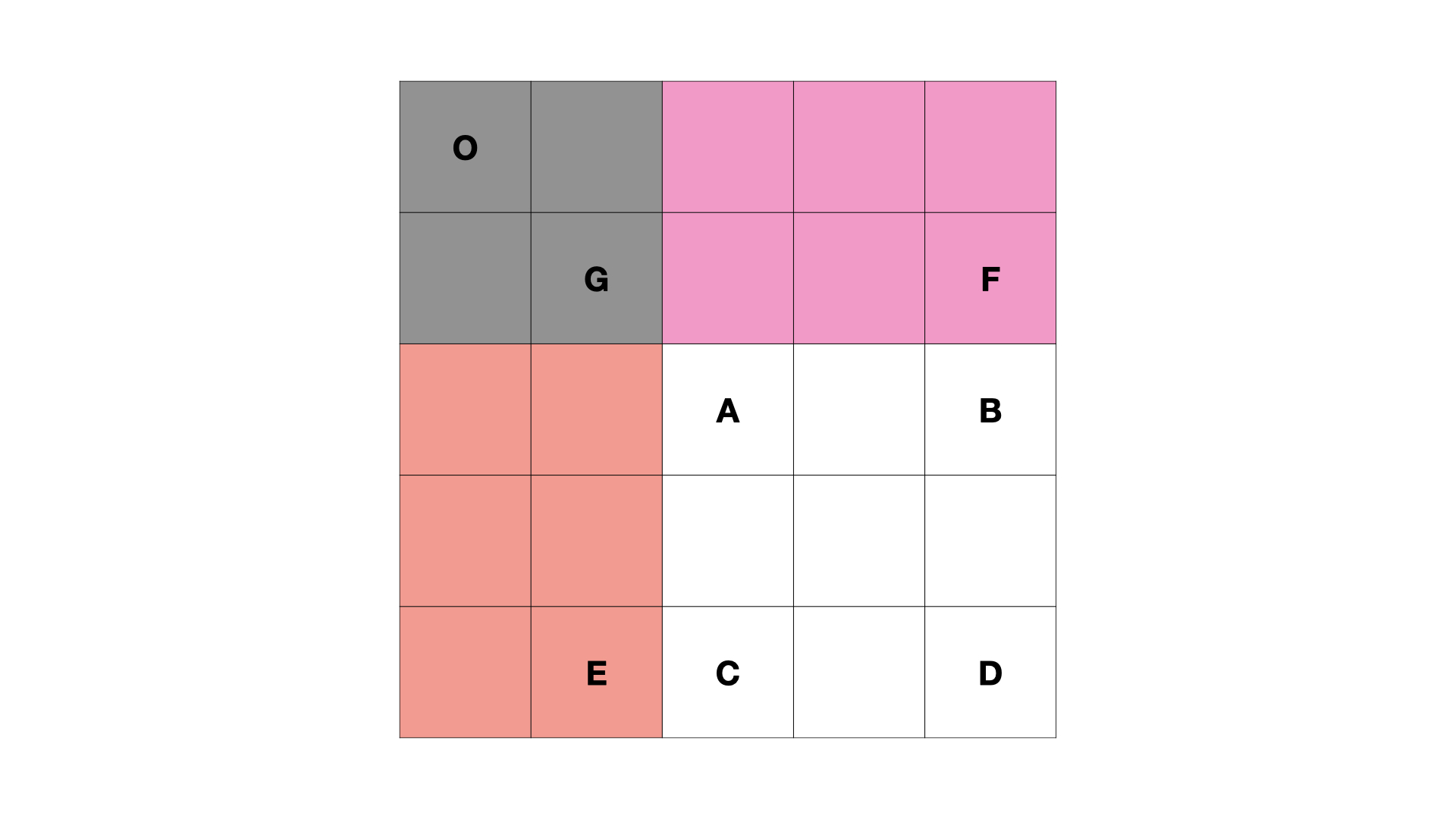
加上子矩形 S ( O , G ) S(O, G) S(O,G) 面积的原因是 S ( O , E ) S(O, E) S(O,E) 和 S ( O , F ) S(O, F) S(O,F) 中都有 S ( O , G ) S(O, G) S(O,G),即减了两次 S ( O , G ) S(O, G) S(O,G),所以需要加上一次 S ( O , G ) S(O, G) S(O,G)。
弄明白这个原理之后,题目就不难解决了。
总结
- 「前缀和」原理非常简单,但却很实用,当遇到「区间和」问题的时候肯定躲不过它。
- 「前缀和」计算方式是对数组进行了预处理,得到了从第 0 0 0 位置到第 i i i 位置的「和」。
- 「前缀和」可以快速求出数组
nums的指定区间 [ i , j ] [i, j] [i,j] 内所有元素的「和」。 - 「前缀和」的复杂度:
- 空间复杂度是 O ( N ) O(N) O(N);
- 初始化的时间复杂度是 O ( N ) O(N) O(N);
- 求「区间和」的时间复杂度是 O ( 1 ) O(1) O(1)。
本文是 《秋招必会的算法题》 系列文章的第一篇,希望对大家有帮助。
你的支持是我继续写下去的动力!求赞,求关注,求转发。我们下期再见!



