归并排序

归并排序

归并排序是将两个有序的数组归并成一个更大的有序数组，要对一个数组排序，可以先不断递归地将数组分为两半进行排序，最后再将结果归并起来。归并排序最吸引人的性质是它能保证任意长度为N的数组所需时间和NlogN成正比，它的主要缺点是它所需的额外空间和N成正比。

图1-1的树状图显示了要将arr[0]到arr[6]，7个元素的数组排序，归并排序的分治思想会先将整个数组通过递归不断拆解成一个个小数组进行归并，再将两两已经排序好的小数组再进行归并排序，一直到整个数组排序完毕。

　　　　　　　　　　　　　　　　　图1-1

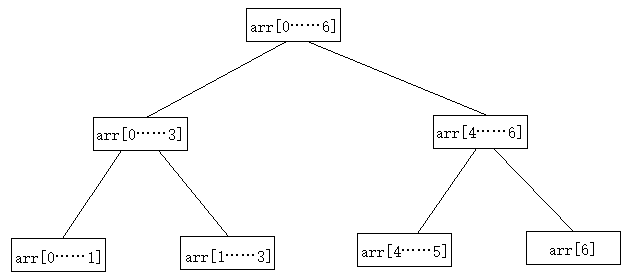
 从图1-1可以看出，如果一棵树正好有n层，对于0到n-1之间的任意k，自顶向下的第k层有2^k个子数组，每个数组长度为2^n-k，归并最多需要2^n-k次比较，因此每层的比较次数为2^k*2^n-k=2ⁿ，n层总共为n2ⁿ=Nlog(N)，因此，归并排序的时间复杂度为O(nlogn)

 

代码1-2为归并排序的C语言实现

#include <stdio.h>

void sort( int arr[], int tmp_arr[], int left, int right );


void merge( int arr[], int tmp_arr[], int left, int mid, int right );


void sort( int arr[], int tmp_arr[], int left, int right )
{
	int mid = (left + right) / 2;
	if ( left >= right )
	{
		return;
	}
	sort( arr, tmp_arr, left, mid );
	sort( arr, tmp_arr, mid + 1, right );
	merge( arr, tmp_arr, left, mid, right );
}


void merge( int arr[], int tmp_arr[], int left, int mid, int right )
{
	int i = left, j = mid + 1, k = 0, len = right - left + 1;
	for ( k = left; k <= right; k++ )
	{
		tmp_arr[k] = arr[k];
	}
	k = left;
	while ( i <= mid && j <= right )
	{
		if ( tmp_arr[i] > tmp_arr[j] )
		{
			arr[k] = tmp_arr[j++];
		}else{
			arr[k] = tmp_arr[i++];
		}
		k++;
	}
	while ( i <= mid )
	{
		arr[k++] = tmp_arr[i++];
	}
	while ( j <= right )
	{
		arr[k++] = tmp_arr[j++];
	}
}


void main()
{
	int	i	= 0;
	int	arr[]	= { 1, 10, -5, 9, 8, 7, 3 };
	int	len	= sizeof(arr) / sizeof(arr[0]);
	int	tmp_arr[len];
	printf( "待排序数组:" );
	for ( i = 0; i < len; i++ )
	{
		printf( "%d ", arr[i] );
	}
	printf( "\n" );
	sort( arr, tmp_arr, 0, len - 1 );
	printf( "排序后数组:" );
	for ( i = 0; i < len; i++ )
	{
		printf( "%d ", arr[i] );
	}
}

　

代码1-3位归并排序的Java实现

import java.util.Arrays;

public class Merge {

	public static void merge(int[] arr, int[] tmpArr, int left, int mid, int right) {
		int i = left, j = mid + 1, k = 0;
		for (k = left; k <= right; k++) {
			tmpArr[k] = arr[k];
		}
		k = left;
		while (i <= mid && j <= right) {
			if (tmpArr[i] > tmpArr[j]) {
				arr[k] = tmpArr[j++];
			} else {
				arr[k] = tmpArr[i++];
			}
			k++;
		}
		while (i <= mid) {
			arr[k++] = tmpArr[i++];
		}
		while (j <= right) {
			arr[k++] = tmpArr[j++];
		}
	}

	public static void sort(int[] arr, int[] tmpArr, int left, int right) {
		if (left >= right) {
			return;
		}
		int mid = (left + right) / 2;
		sort(arr, tmpArr, left, mid);
		sort(arr, tmpArr, mid + 1, right);
		merge(arr, tmpArr, left, mid, right);
	}

	public static void main(String[] args) {
		int[] arr = { 1, 10, -5, 9, 8, 7, 3 };
		int[] tmpArr = new int[arr.length];
		System.out.print("待排序数组:" + Arrays.toString(arr));
		System.out.println();
		sort(arr, tmpArr, 0, arr.length - 1);
		System.out.println("排序后数组:" + Arrays.toString(arr));
	}

}

　　

代码1-4为归并排下序的Python实现

# coding:utf-8
def merge(left, right):
    i, j = 0, 0
    result = []
    while i < len(left) and j < len(right):
        if left[i] > right[j]:
            result.append(right[j])
            j += 1
        else:
            result.append(left[i])
            i += 1
    result += left[i:]
    result += right[j:]
    return result


def sort(arr):
    if len(arr) <= 1: return arr
    mid = int(len(arr) / 2)
    left = sort(arr[:mid])
    right = sort(arr[mid:])
    return merge(left, right)


arr = [1, 10, -5, 9, 8, 7, 3]
print "待排序数组:", arr
print "排序后数组", sort(arr)

　　

代码1-5为归并排序的Scala实现

import java.util.Arrays

object Merge {

  def sort(comparator: (Int, Int) => Boolean)(list: List[Int]): List[Int] = {
    val mid = list.size / 2
    if (mid == 0) list
    else {
      def merge(xs: List[Int], ys: List[Int]): List[Int] = (xs, ys) match {
        case (Nil, ys) => ys
        case (xs, Nil) => xs
        case (x :: nxs, y :: nys) =>
          if (comparator(x, y)) y :: merge(xs, nys)
          else x :: merge(nxs, ys)
      }
      val (left, right) = list splitAt mid
      merge(sort(comparator)(left), sort(comparator)(right))
    }
  }

  def main(args: Array[String]): Unit = {
    val list = List(1, 10, -5, 9, 8, 7, 3)
    println("待排序数组:" + Arrays.toString(list.toArray))
    println("排序后数组:" + Arrays.toString(sort(_ > _)(list).toArray))
  }
}