数据拟合曲线_LMFit(GaussianModel )

今天，我们来谈一谈曲线拟合，想了很久要不要记录一下数据拟合曲线这个问题，最近又遇到了，还是决定浅浅记录一下，以免遗忘。

　　主要还是说一下类似双峰的曲线或者形状怪异的曲线怎么进行拟合。

首先说一下，在数据拟合的时候，往往遇到的曲线并非常规曲线，此时会发现，基本函数无法完美拟合，经过多方资料查找，Python有个LMFit可以拟合多个不同的常规函数形成的曲线，比如说一个双峰的曲线拟合为两个正态分布，形状怪异的曲线由两个正态加上幂函数进行拟合，那么这种情况要怎么去一步一步走呢？

注意：①此文章不是常规函数拟合（三次，幂函数，正态，二次），讲述的是混合曲线的拟合。（方法不一定最好，更好的方法还需要再查阅）

　　　②主要是看拟合思想，提供一个思路，因为也是一个类似三方包一样的，我们需要调参，在工作或者学习中，遇到，能解决实际问题就比较好，深究具体的可能需要研究底层逻辑。

 

当我们拿到一个数据样本，画出了它的分布图，发现偏峰正态还是双峰，但是较低峰的峰值也不是非常明显，我们第一反应可能是拟合一个正态。此时又发现，正态分布呈偏态，可能拟合出来不能贴合图形。

一、LMFit中有个GaussianModel 可以直接帮我拟合两个双峰的曲线，但是需要注意，GaussianModel 很吃初始（initial）参数，需要我们自己先看一下起始的峰值点以及幅度。

 

二、曲线拟合步骤：

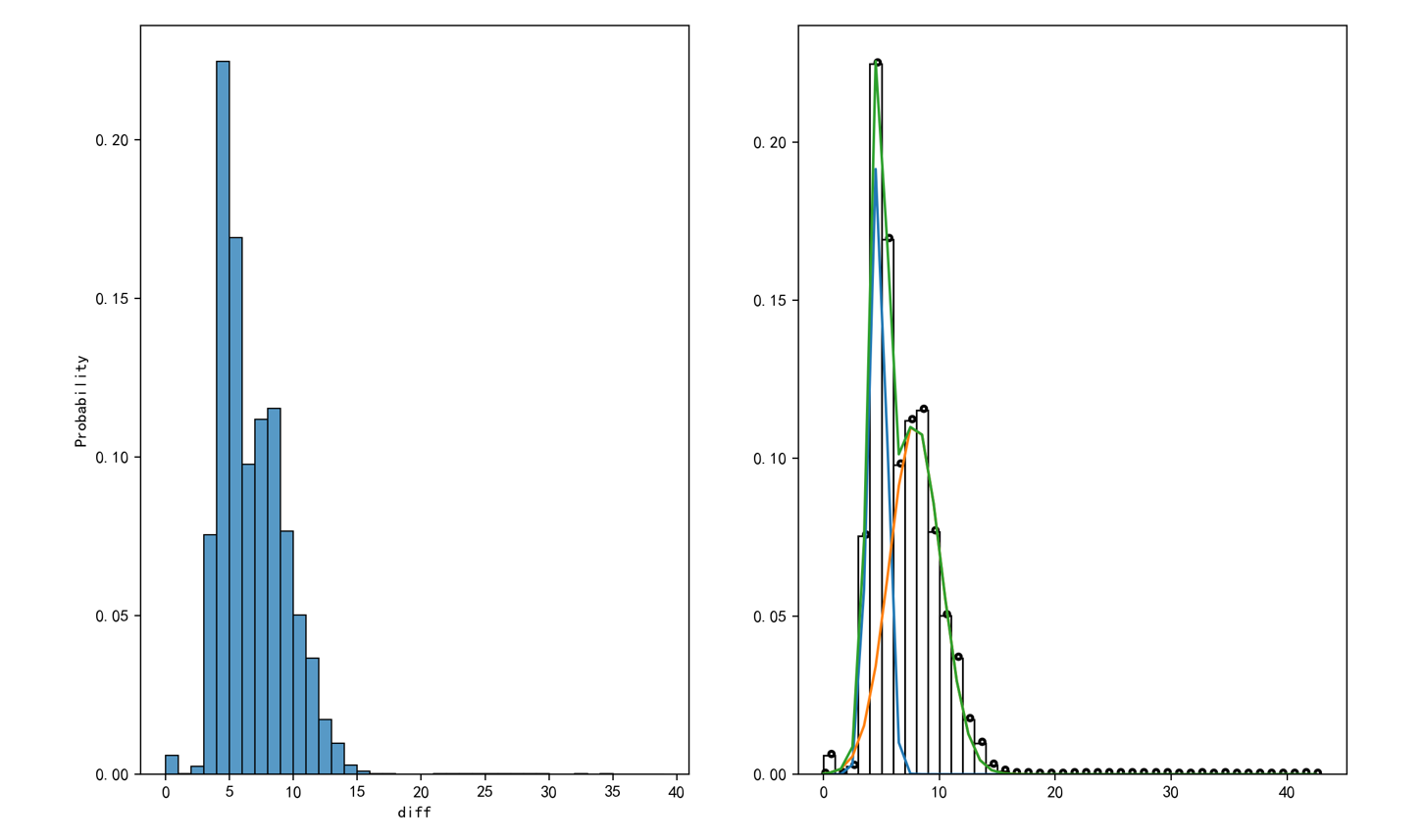
　　1.拿到数据，画出直方图，观测数据分布情况。

　　2.确定双峰分布，画出每个柱子的中心点位置，进行中点拟合。

　　3.LMFit-GaussianModel 拟合，能够看到分布两条曲线就是拟合两个正态分布。

 

三、代码及注释

　　

"""
-*- coding: utf-8 -*-
@FileName: Gaussian.py
@Software: PyCharm
@Time    : 2023/7/18 11:20
@Author  : Panda
"""

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from lmfit.models import GaussianModel


def get_gaussianmodel(all_data):
    # 返回柱子数以及柱子所对应的频数（hist, bins）
    hist, bins = np.histogram(all_data, bins=range(0, 45), density=False)
    # 取出每个柱子的中点，diff为差分
    x = bins[:-1] + np.diff(bins)/2
    # 算出每个柱子的概率密度，每个柱子的频数除以总数
    y = hist / np.sum(hist)
    # 画出申明
    fig, ax = plt.subplots(1, 2, figsize=(12.8, 8))
    # 画出数据分布直方图， 第一个图的直方图
    sns.histplot(all_data, bins=range(0, 40), ax=ax[0], stat="probability")
    # LMFit模型申明，可以两个写在一起，也可以分开写，申明认为是两个高斯曲线拟合成的
    model = (GaussianModel(prefix='g1_') + GaussianModel(prefix='g2_'))
    # 模型拟合参数，先观察一下大致的峰值和幅度，设置初始值
    params = model.make_params(
                            g1_amplitude=0.5,
                            g1_center=5,
                            g1_sigma=1,
                            g2_amplitude=0.5,
                            g2_center=10,
                            g2_sigma=0.6)
    # 拟合高斯模型
    result = model.fit(y, params, x=x)
    # 预测模型的一些报告，可能会告诉你有些参数不可用，和拟合程度，看拟合的结果参数
    print(result.fit_report(min_correl=0.5))
    # 常见的用于分析模型预测结果的函数或属性
    comps = result.eval_components(x=x)
    # 画出第二个图的直方图
    ax[1].hist(bins[:-1], bins, weights=y, color='w', ec='k')
    # 拟合的第一个高斯曲线
    ax[1].plot(x, comps['g1_'], label=r'Gaussian #1, 3-$\sigma$ band')
    # 拟合的第二个高斯曲线
    ax[1].plot(x, comps['g2_'], label=r'Gaussian #2, 3-$\sigma$ band')
    # 拟合的两个结合的总体曲线
    ax[1].plot(x, comps['g1_'] + comps['g2_'], label=r'Gaussian #3, 3-$\sigma$ band')
    # 画出了拟合的中心散点
    ax[1].scatter(x, y, marker="$\circ$",c='k')

 

四、具体的拟合结果解释

 result.fit_report(min_correl=0.5)输出：分为4个部分

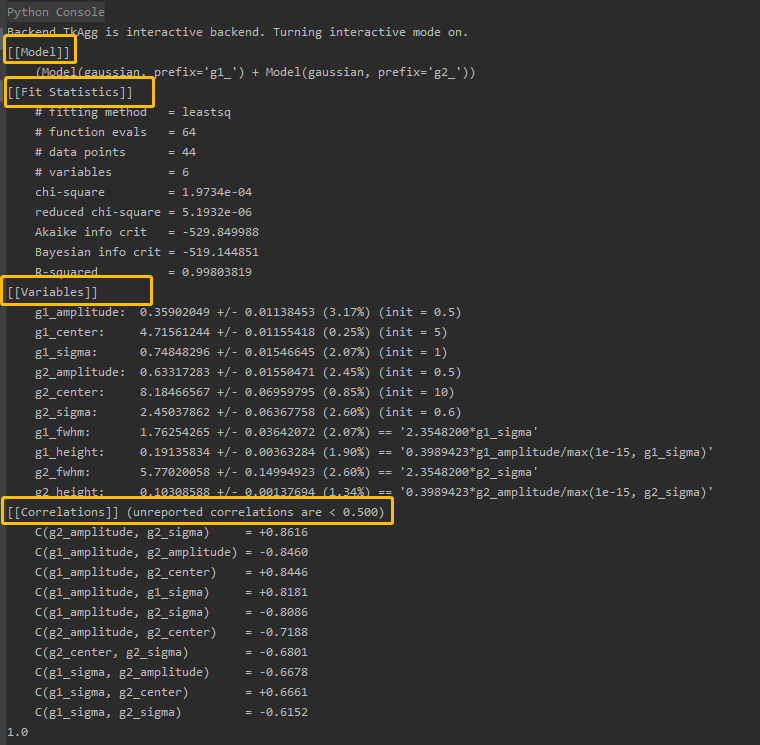
 1. [[Model]]：你的混合模型所使用的是什么函数，此处两个写在了一起，就会分别显示两个

 2.[[Fit Statistics]]：函数拟合的统计结果：

　　# fitting method = leastsq：拟合的方法-最小二乘法

　　# function evals = 64
　　# data points = 44：数据总点数
　　# variables = 6：变量个数
　　chi-square = 1.9734e-04：卡方值，用于度量实际的观测值与理论值之间的差异，此值越小越好。
　　reduced chi-square = 5.1932e-06：缩减卡方值，是将卡方值除以参数数目得到的值，用于考虑模型的自由度。
　　Akaike info crit = -529.849988：赤池信息准则是模型比较准则，用于选择最佳模型。这些准则越小表示模型拟合得越好。
　　Bayesian info crit = -519.144851：贝叶斯信息准则， 这些准则越小表示模型拟合得越好。
　　R-squared = 0.99803819：R平方，R-squared（拟合优度）是用于评估回归模型拟合优度的统计量，此值越接近1说明模型越贴合实际值。

3.[[Variables]]：拟合初始参数值，返回拟合曲线最好的mean+-std(均值+-标准差)，以及你给定的初始值

 

[拟合结果]：[绿色表示整体拟合曲线，黄色和蓝色表示分别拟合曲线，有部分可能重合，导致只显示绿色] —— 2023-7-19修改