洛谷 U141384 电路
洛谷 U141384 电路
题目背景
SeawaySeawa**y是热爱学习的好孩子。
有一天,SeawaySeawa**y正在向他的物理老师LSPLSP讨教物理。LL老师向他介绍了一种神奇的电路,逻辑电路:
LL老师说:逻辑电路是一种离散信号的传递和处理、以二进制为原理、实现数字信号逻辑运算和操作的电路。分组合逻辑电路和时序逻辑电路。前者由最基本的“与门”电路、“或门”电路和“非门”电路组成,其输出值仅依赖于其输入变量的当前值,与输入变量的过去值无关——即不具记忆和存储功能;后者也由上述基本逻辑门电路组成,但存在反馈回路——它的输出值不仅依赖于输入变量的当前值,也依赖于输入变量的过去值。逻辑电路广泛应用于计算机、数字控制、通信、自动化和仪表等方面。
比如,下图就是一张逻辑电路的电路图:
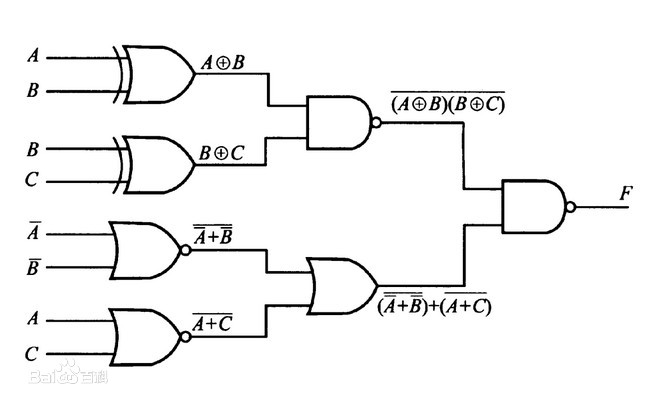
SeawaySeawa**y瞪大了眼睛:太奇妙啦!突然,他的脑中灵光一闪,想到了一个问题......
题目描述
SeawaySeawa**y把任何一套逻辑电路都归为五种基本元件和若干导线。其中,五种基本原件分别是与门(\text{AND}AND),或门(\text{OR}OR),非门(\text{NOT}NOT),异或门(\text{XOR}XOR)和终端(\text{IN}IN)。除终端之外,每个原件有两个入端和一个出端,其作用是把两个入端进入的信号进行逻辑运算,逻辑运算种类和原件种类相同,然后将结果信号输出给出端。信号只有0/10/1两种。终端比较特殊,它自带一种可变信号且只有一个出端,显然,它会把这个信号直接输出给出端。
按照题目背景的描述,显然地,按这种形式、用原件和导线组合成的逻辑电路属于组合逻辑电路。我们限制:整个电路最终只能有一个出端。显然地,如果所有终端的信号被唯一确定,那么整个电路的出端所输出的信号也会被唯一确定。
现在,SeawaySeawa**y的问题是:对于一个给定的组合逻辑电路,每次只改变其中的一个终端的自带信号后,整个电路的出端信号会输出什么信号。
输入格式
从文件circuit.incircuit.i**n中读入数据。
第一行包含一个整数NN。表示原件数量。原件从1-N1−N编号。我们令11号原件的出端为整个电路的出端。数据保证11号原件不会为终端,所有原件都在同一个逻辑电路中。
接下来NN行,每一行描述一个原件,描述规则如下:
首先是一个字符串optopt,为\text{AND,OR,XOR,NOT,IN}AND,OR,XOR,NOT,IN,表示原件种类。
如果原件不为终端,那么接下来两个整数s1,s2s1,s2,表示当前原件的入端所链接的原件编号。
如果原件为终端,那么接下来一个整数p\in[0,1]p∈[0,1],表示终端的初始自带信号种类。
输出格式
输出到文件circuit.outcircuit.out中。
一个0/10/1串,从左到右的每一位表示按编号顺序依次改变每个终端的自带信号后,终端输出信号的种类。
命题背景:
这题我觉得差不多真够我吹一阵子。
题面出奇的精美,爱了爱了。
反差萌->学弟。
题解:
好像还是给了30pts的暴力吧。\(O(n^2)\)的。听学长说优化优化暴力可以打\(O(n^2/32)\)的,好像是用bitset玄学优化优化,不太懂。
然后70分是随机数据,不会出现链卡你,所以这时枚举路径,跑不满\(O(n\log n)\),非常可观。
不难发现:如果一个叶子节点被更改影响到,那么可以肯定的是,这个叶子节点到根节点的链(这个链是唯一的)的所有值都会被取反。那么我们来看这些操作,当操作为非或者异或的时候,那么这个节点的值会被取反(任意一个儿子被修改即可)。反之,如果操作为与或或,必须两个儿子的值都被修改,才能被取反。 但是这道题一次只修改一个叶子节点,所以不存在这种情况。
所以在每个点打一个标记数组,表示这个点会不会随着儿子节点的权值变化而变化,然后维护一个标记数组,从上到下深搜表示这个变化会不会使得父亲节点有变化。然后下传这个标记,最后输出对应的答案就好,整个复杂度是\(O(n)\)的。
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=1e6+10;
int n,ans[maxn],opt[maxn],son[maxn][2],val[maxn];
bool v[maxn];
int turn(char s[])
{
if(s[0]=='I')
return 1;
if(s[0]=='N')
return 2;
if(s[0]=='O')
return 3;
if(s[0]=='A')
return 4;
if(s[0]=='X')
return 5;
}
int dfs1(int u)
{
if(opt[u]==1)
return val[u];
if(opt[u]==2)
return(val[u]=!dfs1(son[u][0]));
if(opt[u]==3)
return(val[u]=(dfs1(son[u][0])|dfs1(son[u][1])));
if(opt[u]==4)
return(val[u]=(dfs1(son[u][0])&dfs1(son[u][1])));
if(opt[u]==5)
return(val[u]=(dfs1(son[u][0])^dfs1(son[u][1])));
}
void dfs2(int u)
{
if(v[u]==0)
v[son[u][0]]=v[son[u][1]]=0;
else
{
switch(opt[u])
{
case 2:
v[son[u][0]]=1;
break;
case 3:
if(val[son[u][0]])
v[son[u][1]]=0;
else
v[son[u][1]]=1;
if(val[son[u][1]])
v[son[u][0]]=0;
else
v[son[u][0]]=1;
break;
case 4:
if(!val[son[u][0]])
v[son[u][1]]=0;
else
v[son[u][1]]=1;
if(!val[son[u][1]])
v[son[u][0]]=0;
else
v[son[u][0]]=1;
break;
case 5:
v[son[u][0]]=v[son[u][1]]=1;
break;
}
}
v[0]=0;
if(son[u][0])
dfs2(son[u][0]);
if(son[u][1])
dfs2(son[u][1]);
}
int main()
{
memset(v,1,sizeof(v));
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
char s[10];
scanf("%s",s);
opt[i]=turn(s);
if(opt[i]==1)
scanf("%d",&val[i]);
else if(opt[i]==2)
scanf("%d",&son[i][0]);
else
scanf("%d%d",&son[i][0],&son[i][1]);
}
dfs1(1);
v[1]=1;
dfs2(1);
for(int i=1;i<=n;i++)
if(opt[i]==1)
printf("%d",val[1]^v[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号