浅谈网络最大流
浅谈网络最大流
本篇随笔简单讲解一下网络流中的网络最大流。
由于这是本蒟蒻的网络流第一篇讲解,所以也会连带介绍网络流的一些基本概念等问题。在后续的网络流讲解中(如果没退役还有的话),就会直接链接引到本篇博客。
本篇讲解的部分图片摘自知乎@Pecco、博客园@chc_1234567890,以及互联网。感谢各路大佬的支持。希望共同进步。
一、网络最大流的一些基本概念
首先,网络流的基本概念。
分为两个部分:网络和流(。。。)
网络的本质是一张带边权有向图。其中有一个点被称作源点,一个点被称作汇点。边权被称为这条边的容量。比如下图。

然后流这个东西需要我们感性理解一下。这个网络可以被抽象成很多生活中的具体事物。比如我们把它抽象成水流,把网络想象成一个自来水管道网,那么流就像是水,每条边的流不能超过容量。
那么什么是网络最大流呢?
还是按上面的方法抽象,顾名思义,网络最大流肯定要求一个类似于最大流量的东西。所以这个问题实际上就是:假定源点流出的水无限多,求进入汇点的最大流量。
二、网络流的实现原理
网络流就是带反悔的贪心。——LLQ
因为要找最大,所以肯定要在当前状态下找一个最优的抉择。那么我们自然而然地觉得应该是每次选容量最大的边去继续流。
所以我们设计了一个找增广路的算法,其基本思路是贪心。
还是拿这张图举例:

增广路,是从源点到汇点的路径,其上所有边的残余容量均大于0。
上图中我首先选择1->2->3,这是一条增广路,提供2流量;然后我们相应地扣除选择路径上各边的容量,1->2的容量变成1,2->3的容量变成0,这时的容量称为残余容量。然后我们再找到1->2->4->3这条路径,按残余容量计算流量,它提供1流量(选择这两条路的顺序可以颠倒)。1->2->4->3也是一条增广路。
但是这个贪心并不对。有可能我们流到当前点是最优的,但是当前点到汇点有一个容量非常小的边,卡掉了,所以不如两条边都走,有可能更大。
比如下面这个例子:
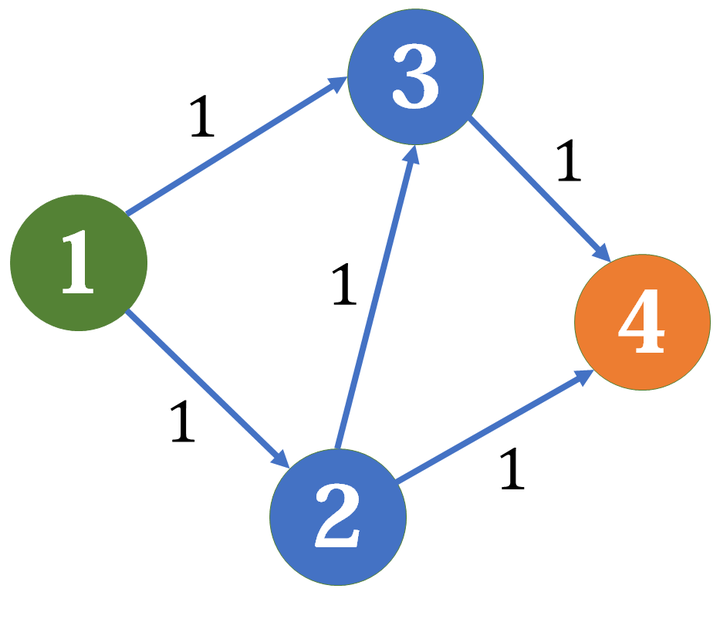
我们找到一条增广路,其残余网络变成这样:
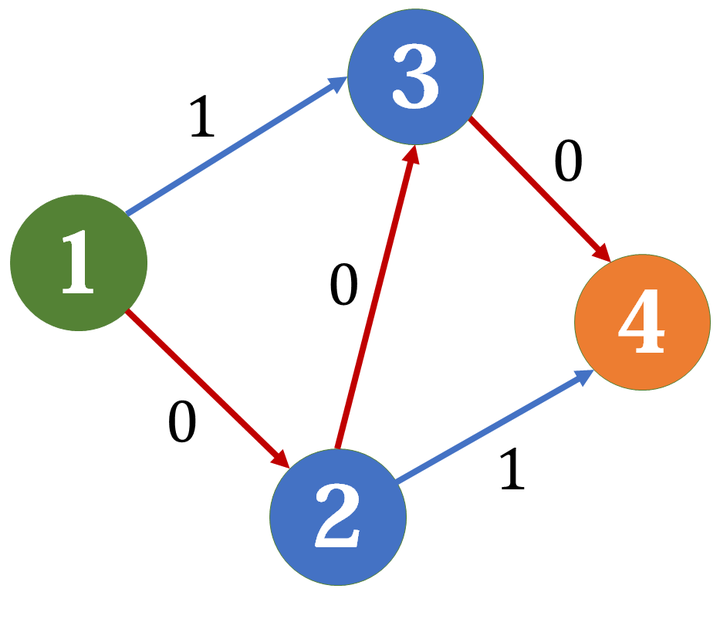
于是我们求得最大流为1.但这显然不对,这就是我们刚刚分析的贪心错误的情况。
于是我们引入:带反悔的贪心。
具体说来,就是在每条边上建立反向边,作为“反悔边”。这些边的妙用会在下面提到。
比如上面的贪心错误的例子,建好反悔边:
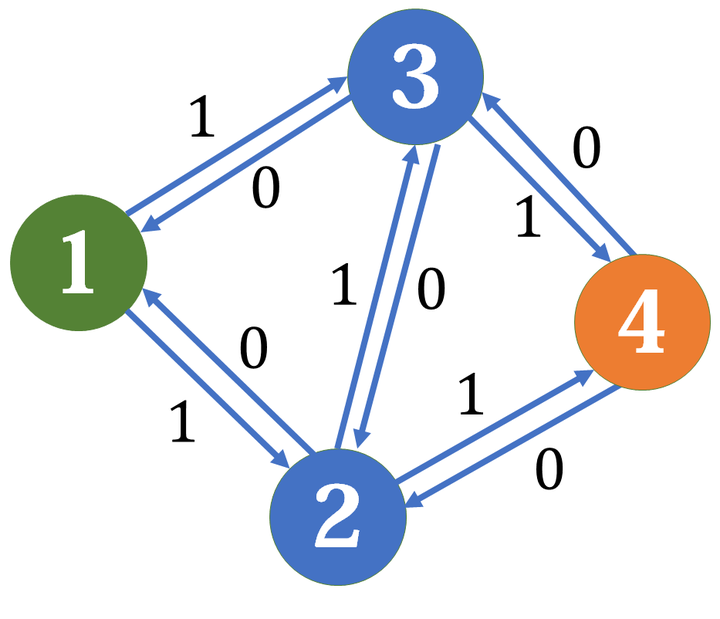
在我们找增广路、扣除流量的同时,要把反向边加上相同的流量,以备反悔。这样,在找到一条增广路之后,剩下的参与网络还是可以找到增广路:
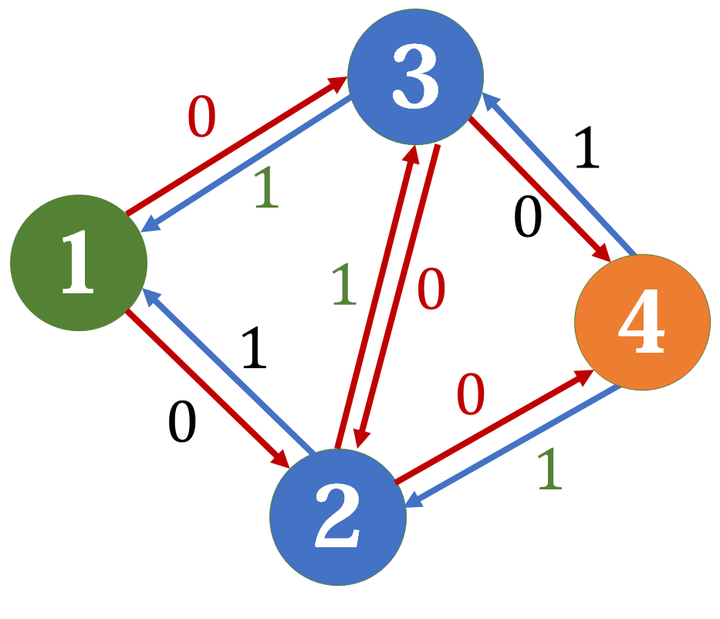
这样,我们隐隐约约地感悟到,反向建边其实是一种“撤销”,通过这种撤销,我们就把之前走过这条边的一些流量拉了回去。所以反向边容量其实是“可以撤回的量”。
所以叫可反悔贪心。
这样的话,我们就可以保证当找不到增广路的时候,流到汇点的流量就是最大流量了。
三、最大流的代码实现
网络流包括很多算法。这种最大流是一种算法,还有之后的费用流,上下界流等。
刚刚我们讲到的算法叫做FF算法,也叫\(Ford-Fulkerson\)算法。这个算法的实现基于深搜。
借助例题:洛谷模板讲解代码。
#include<cstdio>
#include<algorithm>
#include<cstring>
#define int long long
using namespace std;
const int maxn=210;
const int maxm=5010;
const int INF=1e9;
int n,m,s,t;
int tot=1,to[maxm<<1],nxt[maxm<<1],head[maxn],val[maxm<<1];
bool v[maxn];
void add(int x,int y,int z)
{
to[++tot]=y;
nxt[tot]=head[x];
val[tot]=z;
head[x]=tot;
}
int dfs(int x,int flow)
{
if(x==t)
return flow;
v[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(val[i]==0||v[y])
continue;
int tmp=0;
if((tmp=dfs(y,min(val[i],flow)))>0)
{
val[i]-=tmp;
val[i^1]+=tmp;
return tmp;
}
}
return 0;
}
signed main()
{
scanf("%lld%lld%lld%lld",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{
int x,y,z;
scanf("%lld%lld%lld",&x,&y,&z);
add(x,y,z);
add(y,x,0);
}
int ans=0,tmp=0;
while((tmp=dfs(s,INF))>0)
{
memset(v,0,sizeof(v));
ans+=tmp;
}
printf("%lld\n",ans);
return 0;
}
其实是对上面过程的模拟,每次深搜找增广路。\(v\)数组来保证节点不会被重复经过。然后存储对边来进行反悔边的权值修改。
这个算法的复杂度是\(O(mf)\),其中\(m\)是边数,\(f\)是最大流。这个复杂度竟然和流量有关,就很玄学。所以并不稳定,一般也不会用它。就是抛砖引玉。(上面的代码只有80pts)
还有一个EK算法,全称是Edmond-Karp算法。
EK算法较之FF算法的时间复杂度较优。是\(O(nm^2)\)级别的,其原理是把刚刚的DFS实现找增广路变成BFS实现找增广路。这样的话,其不可能会绕远路,每次找到的都是最短的增广路。
这时,由于我们不知道我们到底选择了哪条增广路,所以不能再BFS的同时对边进行反悔更新。这时,就需要我们记录一个pre数组,表示点的前驱边,这样,就能通过到达汇点后的原路返回更新这些边。
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define int long long
using namespace std;
const int maxn=210;
const int maxm=5010;
const int INF=1e18;
int n,m,s,t;
int tot=1,to[maxm<<1],nxt[maxm<<1],head[maxn],val[maxm<<1];
int flow[maxn],pre[maxn];
bool v[maxn];
void add(int x,int y,int z)
{
to[++tot]=y;
nxt[tot]=head[x];
val[tot]=z;
head[x]=tot;
}
bool bfs()
{
memset(pre,-1,sizeof(pre));
queue<int> q;
q.push(s);
flow[s]=INF;
while(!q.empty())
{
int x=q.front();
q.pop();
if(x==t)
break;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(val[i]==0||pre[y]>0)
continue;
pre[y]=i;
flow[y]=min(flow[x],val[i]);
q.push(y);
}
}
return pre[t]!=-1;
}
signed main()
{
scanf("%lld%lld%lld%lld",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{
int x,y,z;
scanf("%lld%lld%lld",&x,&y,&z);
add(x,y,z);
add(y,x,0);
}
int ans=0;
while(bfs())
{
ans+=flow[t];
for(int i=t;i!=s;i=to[pre[i]^1])
{
val[pre[i]]-=flow[t];
val[pre[i]^1]+=flow[t];
}
}
printf("%lld\n",ans);
return 0;
}
这份代码已经可以得到满分的好成绩。
以及最常用(因为最快)的Dinic算法
这个算法涉及到一种优化——当前弧优化。
因为这个优化,所以这种算法我们用一篇博客单讲。这里直接引入博客链接:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号