重谈树状数组
重谈树状数组
蒟蒻在2019年7月31号就浅谈过一波树状数组。那时的自己还是萌新虽然现在也很菜。对位运算的理解、对树状数组的理解、对权值数据结构的理解都不是很深。然后还敢瞎浅谈。虽然谈的没什么太大错误。但是其实一直都没有对这个数据结构有很深的理解或者造诣。很多时候相同功能的操作宁可去拍一发线段树。因为树状数组心里一直没底。这应该是个很不好的习惯。
所以今天来重新谈一遍树状数组。加深理解,克服恐惧,学会应用。
一、树状数组的功能
其实树状数组被归为简单数据结构,其本身并没有多难。
其维护的东西也非常简单,是前缀和。也就是其本身只能维护\([1,x]\)这样的区间,但是根据前缀和的差分性,求两次一减,也可以求出任意区间的和。
也就是说,树状数组是区间求和的一个数据结构。其支持的功能有区间求和(其实是两次前缀和相减,其基本功能只有求前缀和)、单点修改。
树状数组与线段树的比较
有人说线段树支持所有树状数组的操作,这没问题。线段树也支持区间求和、单点修改。不仅如此,线段树较之树状数组,还有得天独厚的优势:区间修改。也就是著名的懒标记。所以本蒟蒻一直以为会了线段树就不再需要树状数组。但是其实事实并非如此。
树状数组的常数很小,而且码量少,便于调试。很多时候这个便于调试能够救命。
二、树状数组的原理
现在我们知道树状数组是查前缀和的。
前缀和正常的维护方式是O(n)遍历,为了优化这一点,我们必须把原先的一个一个加变成一堆一堆加。
分块!
那么怎么一堆一堆加能保证不会乱呢?那么我们就需要找到任何一个数的唯一分解方式。说到这里,答案已经呼之欲出了,那就是二进制分解。
任何一个整数都可以被拆成不重复的2的整数次幂。那么我们就可以根据这个2的整数次幂把一个数拆成不超过log级别的块,以实现O(log n)的复杂度进行查询。
以7为例,7可以按如上方式被拆成\([1,4],[5,6],[7,7]\)。
为什么这么拆呢?
\(7\)的二进制是:\((111)_2\)。那么其就会被拆成长度为1、长度为2、长度为4的三个小块,从上往下分解,就是\([7,7],[5,6],[1,4]\)。
于是我们发现,每次取当前的数的最低一位1所代表的长度,依次递减,与此同时,在树状数组的对应位置把数加到答案,最后减到0的时候,我们就得到了我们想要的答案。
依然来一波原图:
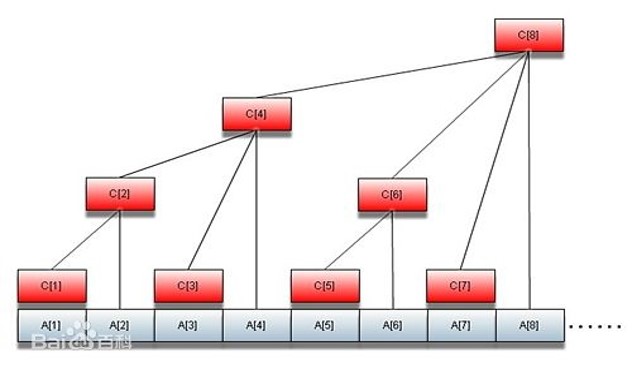
三、树状数组的实现
我们发现,依次取最后的1的操作不就是lowbit嘛?
关于lowbit操作,请走:浅谈lowbit运算
那么在实现的过程中,每次加当前数,之后取当前数的lowbit,减去。重复这个过程,就可以做到在log的时间范围内求出前缀和。
代码实现由于是重谈,就不示范了,大家自己随便搜搜都能找到。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号