NOI 2013 树的计数
NOI 2013 树的计数
题目描述
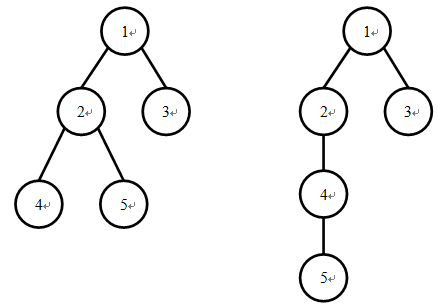
我们知道一棵有根树可以进行深度优先遍历（DFS）以及广度优先遍历（BFS）来生成这棵树的 DFS 序以及 BFS 序。两棵不同的树的 DFS 序有可能相同，并且它们的 BFS 序也有可能相同，例如下面两棵树的 DFS 序都是 1 2 4 5 3，BFS 序都是 1 2 3 4 5。
现给定一个 DFS 序和 BFS 序，我们想要知道，符合条件的有根树中，树的高度的平均值。即，假如共有 KK 棵不同的有根树具有这组 DFS 序和 BFS 序，且他们的高度分别是 h_1, h_2, \ldots, h_Kh1,h2,…,h**K，那么请你输出：
\frac{h_1+h_2+\ldots+h_K}KK**h1+h2+…+h**K
输入格式
第一行包含 11 个正整数 nn，表示树的节点个数。
第二行包含 nn 个正整数，是一个 1 \ldots n1…n 的排列，表示树的 DFS 序。
第三行包含 nn 个正整数，是一个 1 \ldots n1…n 的排列，表示树的 BFS 序。
输入保证至少存在一棵树符合给定的两个序列。
输出格式
输出 11 个实数，四舍五入保留恰好三位小数，表示树高的平均值。
题解：
一开始看到这道题还是没什么思路的。因为感觉没什么办法来通过序列来还原树。反正就是不知道咋暴力。
既然不知道暴力，就去想正解吧。没办法了。
发现，虽然序列还原树没什么思路，但是可以显然地发现一个性质：BFS序分几层，树的高度就是多少。也就是说在BFS序上枚举断点即可。
兴冲冲地去做，发现还不是那么的简单，因为情况大抵有三种：必须分，必须部分，可分可不分。
然后想想如何判断这三种情况。
首先，对于bfs序连续的两个点，不是在同一层，就是在下一层。那么这个条件可以用DFS序约束，如果BFS序连续，但是较大BFS序的DFS序反而较小，那么就一定被挪到下一层去了，这个断点位置的贡献为1.反之，贡献不一定为0，也有可能是0.5，所以确定不了。
想到这里兴高采烈了好半天，但是其实还远远未结束。
因为只考虑了DFS对BFS序的约束，BFS序必然也会对DFS序有约束。
那么，对于DFS序连续的两个点，有可能是父子关系，也有可能都是叶子，是兄弟关系。甚至有可能，是其一个点某一个祖先的儿子。
如果是兄弟关系或者父子关系，那么其BFS序也应该是连续的。也就是它们的深度差不能大于1。它们的BFS序之间最多分1层。这样的话，可以用一个差分来维护区间的这个信息。
差分维护的是分多少层。
但是如果是祖先关系，那么其BFS序就会出现逆序的情况。也就是较大DFS序的BFS序反而较小。
代码：
#include<cstdio>
using namespace std;
const int maxn=3e5+5;
int n;
int bfn[maxn],dfn[maxn],bp[maxn],dp[maxn],s[maxn];
double ans;
int main()
{
freopen("average.in","r",stdin);
freopen("average.out","w",stdout);
scanf("%d",&n);
ans=2;
++s[1];
--s[2];
for(int i=1;i<=n;i++)
{
scanf("%d",&dfn[i]);
dp[dfn[i]]=i;
}
for(int i=1;i<=n;i++)
{
scanf("%d",&bfn[i]);
bp[bfn[i]]=i;
}
for(int i=1;i<=n;i++)
{
dfn[i]=bp[dfn[i]];
bfn[i]=dp[bfn[i]];
}
for(int i=1;i<n;++i)
if(bfn[i]>bfn[i+1])
++s[i],--s[i+1],++ans;
for(int i=1;i<n;++i)
if(dfn[i]+1<dfn[i+1])
++s[dfn[i]],--s[dfn[i+1]];
int w=0;
for(int i=1;i<n;++i)
w+=s[i],ans+=w?0:0.5;
printf("%.3lf\n",ans);
return 0;
}
