CF601B Lipshitz Sequence
CF601B Lipshitz Sequence
题目描述
A function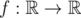 
is called Lipschitz continuous if there is a real constant KK such that the inequality |f(x)-f(y)|<=K·|x-y|∣f(x)−f(y)∣<=K⋅∣x−y∣ holds for all 
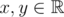. We'll deal with a more... discrete version of this term.
For an array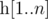 
, we define it's Lipschitz constant 
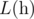as follows:
- if n<2 ,
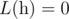
- if n>=2n>=2 ,
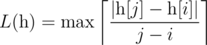over all 1<=i<j<=n
In other words,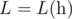 
is the smallest non-negative integer such that |h[i]-h[j]|<=L·|i-j|∣h[i]−h[j]∣<=L⋅∣i−j∣ holds for all 1<=i,j<=n1<=i,j<=n .
You are given an array 
of size nn and qq queries of the form [l,r][l,r] . For each query, consider the subarray 
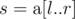; determine the sum of Lipschitz constants of all subarrays of 
.
输入格式
The first line of the input contains two space-separated integers nn and qq ( 2<=n<=1000002<=n<=100000 and 1<=q<=1001<=q<=100 ) — the number of elements in array and the number of queries respectively.
The second line contains nn space-separated integers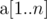 
(
).
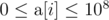The following qq lines describe queries. The ii -th of those lines contains two space-separated integers l_{i}l**i and r_{i}r**i ( 1<=l_{i}<r_{i}<=n ).
输出格式
Print the answers to all queries in the order in which they are given in the input. For the ii -th query, print one line containing a single integer — the sum of Lipschitz constants of all subarrays of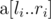 
.
题意翻译
对于一个序列 v[1..n]，当 1<=x<y<=n 且 x,y 均为整数时， 同样满足|v[x]-v[y]|<=K*|x-y|， 则称 K 的最小整数值 为序列 v 的 Lipschitz 常数。 现在给你一个长度为 n 的序列 v[1..n]并给出 q 个询问，对于每对询问[l,r]， 你需要求出 v[l..r]的所有子序列 v[x..y]（l<=x<y<=r）的 Lipschitz 常数之和。
[输入格式] 第一行两个整数 n 和 q， 分别表示序列的长度以及询问的个数。 第二行 n 个数， 表示 v[1..n]， 0<=v[i]<=10^8。 接下来 q 行， 每行两个数 l 和 r， 表示询问的区间为[l..r]。
[输出格式] 对于每个询问， 输出一行一个数， 即 v[l..r]的所有子序列的 Lipschitz 常数之和。
题解：
其实原题面能对思路进行启发，翻译过来毕竟漏掉了很多东西。
其实这个\(Lipshitz\)值是啥啊，就是这个东西呀：
其中，\(i,j\)要遍历所有位置。
这个是啥啊，这个不就是这个散点型函数的斜率么！
于是我们对一个区间进行子区间枚举，并且在子区间再暴力枚举\(i,j\)。就可以暴力地得到这个东西。时间复杂度为\(O(qn^4)\)。可以通过20pts（真是良心出题人）。
然后思考优化。发现可以剪枝呀！
不用枚举那么多，可以证明的一个贪心是：对于任意三个点来讲，其最大斜率绝对不可能出现在一号点和三号点之间，而只会出现在1、2，或2、3之间。
于是先预处理出所有的\(h[i+1]-h[i]\)，然后架一棵线段树求区间max，可以把一重\(n^2\)优化成\(\log n\)。复杂度为\(O(qn^2\log n)\)。可以通过60pts。
还能不能更优秀呢？能，可以换种思路，把问题变成：询问区间中有多少子区间是以\(a[i]\)做最大值的（\(a[i]=|h[i+1]-h[i]|\)）
发现这个可以用单调栈维护出左右第一个大于它的。设左右分别为\(l,r\)，那么最后每个\(a[i]\)对答案的贡献就是，这个点到左的距离*这个点到右的距离 *这个点的权值.
于是我们只需要每次扫一遍即可。
时间复杂度\(O(n+qn)\)。
可以得满分。
#include<cstdio>
#include<cmath>
#define lll long long
using namespace std;
const int maxn=1e5+5;
int n,q;
int h[maxn],a[maxn];
int st[maxn],top;
int cnt[maxn];
lll query(int l,int r)
{
lll ret=0;
top=0;
st[0]=l-1;
for(int i=l;i<r;i++)
{
while(top && a[i]>a[st[top]])
{
ret+=(1ll*cnt[top]*a[st[top]]*(i-st[top]));
top--;
}
st[++top]=i;
cnt[top]=i-st[top-1];
}
while(top)
{
ret+=(1ll*cnt[top]*a[st[top]]*(r-st[top]));
top--;
}
return ret;
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
scanf("%d",&h[i]);
for(int i=1;i<n;i++)
a[i]=abs(h[i+1]-h[i]);
for(int i=1;i<=q;i++)
{
int ll,rr;
scanf("%d%d",&ll,&rr);
printf("%lld\n",query(ll,rr));
}
return 0;
}
