CF1141G Privatization of Roads in Treeland
CF1141G Privatization of Roads in Treeland
题目描述
Treeland consists of nn cities and n-1n−1 roads. Each road is bidirectional and connects two distinct cities. From any city you can get to any other city by roads. Yes, you are right — the country's topology is an undirected tree.
There are some private road companies in Treeland. The government decided to sell roads to the companies. Each road will belong to one company and a company can own multiple roads.
The government is afraid to look unfair. They think that people in a city can consider them unfair if there is one company which owns two or more roads entering the city. The government wants to make such privatization that the number of such cities doesn't exceed kk and the number of companies taking part in the privatization is minimal.
Choose the number of companies rr such that it is possible to assign each road to one company in such a way that the number of cities that have two or more roads of one company is at most kk . In other words, if for a city all the roads belong to the different companies then the city is good. Your task is to find the minimal rr that there is such assignment to companies from 11 to rr that the number of cities which are not good doesn't exceed kk .
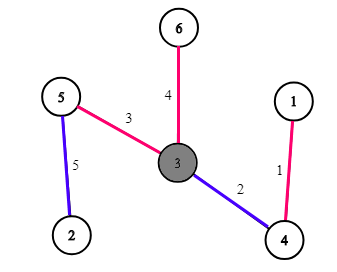 The picture illustrates the first example ( n=6, k=2n=6,k=2 ). The answer contains r=2r=2 companies. Numbers on the edges denote edge indices. Edge colors mean companies: red corresponds to the first company, blue corresponds to the second company. The gray vertex (number 33 ) is not good. The number of such vertices (just one) doesn't exceed k=2k=2 . It is impossible to have at most k=2k=2 not good cities in case of one company.
The picture illustrates the first example ( n=6, k=2n=6,k=2 ). The answer contains r=2r=2 companies. Numbers on the edges denote edge indices. Edge colors mean companies: red corresponds to the first company, blue corresponds to the second company. The gray vertex (number 33 ) is not good. The number of such vertices (just one) doesn't exceed k=2k=2 . It is impossible to have at most k=2k=2 not good cities in case of one company.
输入格式
The first line contains two integers nn and kk ( 2 \le n \le 200000, 0 \le k \le n - 12≤n≤200000,0≤k≤n−1 ) — the number of cities and the maximal number of cities which can have two or more roads belonging to one company.
The following n-1n−1 lines contain roads, one road per line. Each line contains a pair of integers x_ix**i , y_iy**i ( 1 \le x_i, y_i \le n1≤x**i,y**i≤n ), where x_ix**i , y_iy**i are cities connected with the ii -th road.
输出格式
In the first line print the required rr ( 1 \le r \le n - 11≤r≤n−1 ). In the second line print n-1n−1 numbers c_1, c_2, \dots, c_{n-1}c1,c2,…,c**n−1 ( 1 \le c_i \le r1≤c**i≤r ), where c_ic**i is the company to own the ii -th road. If there are multiple answers, print any of them.
题意翻译
Treeland包含n个城市和n-1条道路。每条道路都是双向的,连接两个不同的城市。从任何一个城市你都可以通过公路到达任何其他城市。是的,你是对的——这个国家的拓扑结构是一棵没有方向的树。
在Treeland有一些私人道路公司。政府决定向这些公司出售道路。每条路都属于一家公司,一家公司可以拥有多条道路。
政府害怕看上去不公平。他们认为,如果有一家公司拥有两条或两条以上的进入这个城市的道路,那么这个城市里的人就会认为这是不公平的。政府希望这样不公平的城市数量不超过k,那么最少需要多少个不同的公司来参与投资?
选择公司的数量r,这样就可以将每条道路分配给某家公司,这样一家公司拥有两条或两条以上到达同一个城市道路的城市数量最多为k。(译者注:这里是有一点费脑子,大家多想想)换句话说,如果对一个城市来说,所有的到达这座城市的道路都属于不同的公司,那么这个城市就是好的。你的任务是找到最小的r,然后分配所有道路,使得不太好的城市的数量不超过k。
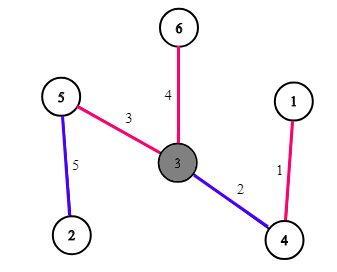
图为第一个例子(n=6,k=2)。答案r=2。边上的数字表示边的编号。边的颜色表示公司:红色为第一个公司,蓝色为第二个公司。灰色顶点(3号)不好。这类顶点的数目(只有一个)不超过k(k=2)。如果有一家公司,在分配合理的情况下,不可能有2个不好的城市。
题解:
不知道为什么是紫题。
非常容易证明贪心。排个序就出来了。
然后染色的话是这道题重点,可以用DFS,在遍历的时候加个参数c保证颜色不重复。
之后把枚举到的原始边编号映射到答案边编号上即可。
代码:
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=2e5+5;
int n,k,r;
int tot,head[maxn],to[maxn<<1],nxt[maxn<<1];
int du[maxn],ans[maxn];
void add(int x,int y)
{
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void coloring(int x,int f,int c)
{
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==f)
continue;
c++;
if(c>r)
c=1;
ans[(i+1)/2]=c;
coloring(y,x,c);
}
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
du[x]++,du[y]++;
}
sort(du+1,du+n+1);
r=du[n-k];
coloring(1,0,0);
printf("%d\n",r);
for(int i=1;i<n;i++)
printf("%d ",ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号