洛谷 P7042 「MCOI-03」正方

洛谷 P7042 「MCOI-03」正方

洛谷传送门

题目背景

MC 中没有圆。

所以小 S 和小 Q 和小 U 和小 A 和小 R 和小 E 喜欢 Square。

题目描述

给定一个正方形，求有多少个正方形内的点满足与正方形四个顶点划分出来的四块面积的比为 a🅱️c:da🅱️c:da🅱️c:d。四个数不分顺序。

比如如下图所示假设一个点 E 使得分成的四个三角形的面积之比为 a🅱️c:da🅱️c:da🅱️c:d，那么这个点 E 就符合要求。因为不分顺序，所以分出来的比是 d🅱️a💿b🅰️cd🅱️a:c 也可以。但是点 E 不是唯一解，你要输出的是解的个数。

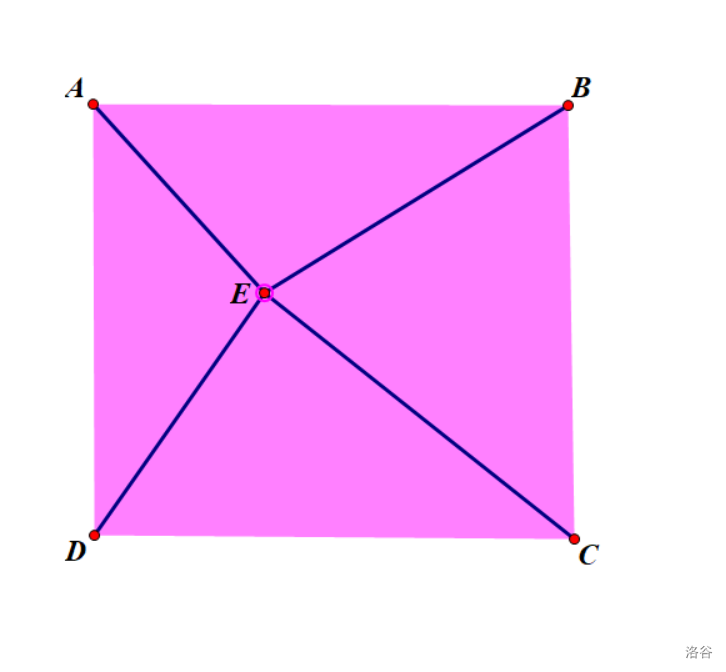
因为小 S 和小 Q 和小 U 和小 A 和小 R 和小 E 很喜欢询问，所以本题给定了 qqq 组询问。

输入格式

第一行一个整数 qqq 代表询问个数。
接下来 qqq 行每行四个整数 a,b,c,da,b,c,da,b,c,d。

输出格式

qqq 行每行一个整数代表答案。

---

题解：

没啥可说的。很容易发现就0，1，4，8这几种答案，直接判即可。

芜湖？T1可放这种题么？

注意C++不能连等......(我是废物)

代码：

#include<cstdio>
#include<algorithm>
#define int long long
using namespace std;
int q;
int a[5];
signed main()
{
	scanf("%lld",&q);
	while(q--)
	{
		for(int i=1;i<=4;i++)
			scanf("%lld",&a[i]);
		sort(a+1,a+5);
		if(a[1]+a[4]!=a[2]+a[3])
		{
			puts("0");
			continue;
		}
		else if(a[1]==a[2]&&a[2]==a[3]&&a[3]==a[4]&&a[4]==a[1])
		{
			puts("1");
			continue;
		}
		else if(a[1]==a[2]&&a[3]==a[4])
		{
			puts("4");
			continue;
		}
		puts("8");
	}
	return 0;
}