CF453A Little Pony and Expected Maximum
CF453A Little Pony and Expected Maximum
题目描述
Twilight Sparkle was playing Ludo with her friends Rainbow Dash, Apple Jack and Flutter Shy. But she kept losing. Having returned to the castle, Twilight Sparkle became interested in the dice that were used in the game.
The dice has mm faces: the first face of the dice contains a dot, the second one contains two dots, and so on, the mm -th face contains mm dots. Twilight Sparkle is sure that when the dice is tossed, each face appears with probability 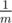 . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice nn times.
. Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice nn times.
输入格式
A single line contains two integers mm and nn ( 1<=m,n<=10^{5}1<=m,n<=105 ).
输出格式
Output a single real number corresponding to the expected maximum. The answer will be considered correct if its relative or absolute error doesn't exceed 10^{-4}10−4 .
题意翻译
暮暮刚刚在和她的朋友——AJ(苹果杰克)、FS(小蝶)、RD(云宝黛西)玩Ludo游戏。但是她马品没攒够总是输。回到城堡过后,她对游戏用的骰子产生了兴趣。
题目描述
这个骰子有M面:骰子的第一面有一个点,第二面有两个点,以此类推,第m面含有M点。暮暮确信的是,当掷骰子时,每一面都有1/m的可能性出现,并且每次投掷的概率都是都是独立的。请你帮助她计算掷N次骰子后每次得到的点数中最大值的期望。
输入输出格式
输入格式:
一行两个整数 m 和 n (1 ≤ m, n ≤ 10^5).
输出格式:
输出一行一个实数,与答案误差不大于10^-4
题解:
对于这种数学期望类的题目,思路往两个方向去:第一种思考可不可以递推地DP转移,也就是我们常说的期望DP。第二种就是直接从期望的定义进行探究,用数学方法推导一个公式然后求解。
这道题首先想到期望DP,但是没有设置出一个比较好的状态来进行转移。
那么直接考虑可不可以推导。
期望的定义:概率乘权值。
那么现在权值已知,我们只需要找每个权值的概率即可。
首先总事件数为\(m^n\),很好理解。
假设扔了n次之后,扔到的最大值是k。那么在这\(m^n\)种情况中,符合要求的情况就是\(k^n-(k-1)^n\)种。
为什么呢?
扔到1-k的情况是\(k^n\),扔到1-(k-1)的情况是\((k-1)^n\),容斥可得。
所以期望就是:
化简可得代码:
注意,不要用long double
#include<cstdio>
#include<cmath>
using namespace std;
double n,m,ans;
int main()
{
scanf("%lf%lf",&m,&n);
for(double i=1;i<=m;i++)
ans+=i*(pow(i/m,n)-pow((i-1)/m,n));
printf("%.12lf\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号