洛谷 AT896 幅優先探索
洛谷 AT896 幅優先探索
题目描述
たかはし君は迷路が好きです。今、上下左右に移動できる二次元盤面上の迷路を解こうとしています。盤面は以下のような形式で与えられます。
- まず、盤面のサイズと、迷路のスタート地点とゴール地点の座標が与えられる。
- 次に、それぞれのマスが通行可能な空きマス(
.)か通行不可能な壁マス(#)かという情報を持った盤面が与えられる。盤面は壁マスで囲まれている。スタート地点とゴール地点は必ず空きマスであり、スタート地点からゴール地点へは、空きマスを辿って必ずたどり着ける。具体的には、入出力例を参考にすると良い。
今、彼は上記の迷路を解くのに必要な最小移動手数を求めたいと思っています。どうやって求めるかを調べていたところ、「幅優先探索」という手法が効率的であることを知りました。幅優先探索というのは以下の手法です。
- スタート地点から近い(たどり着くための最短手数が少ない)マスから順番に、たどり着く手数を以下のように確定していく。説明の例として図1の迷路を利用する。
図1. 説明に用いる盤面- 最初に、スタート地点は、スタート地点から手数0でたどり着ける(当然)ので、最短手数0で確定させる(図2)。
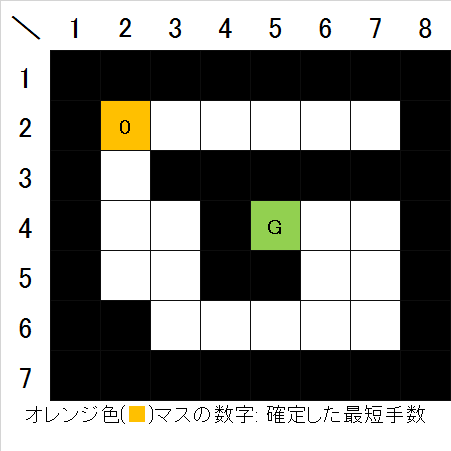図2. 最短手数0でたどり着けるマスが確定(初期)- 次に、スタート地点の四近傍(上下左右)の空きマスについて、手数1で確定させる(図3)。
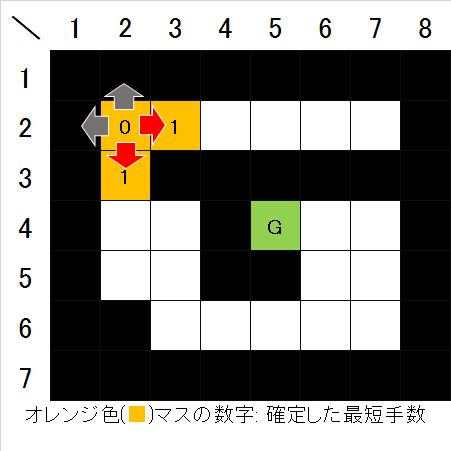図3. 最短手数1でたどり着けるマスが確定- 次に、手数1で確定したそれぞれのマスの4近傍を見て、まだ確定していない空きマスがあればそのマスを手数2で確定させる(図4)。
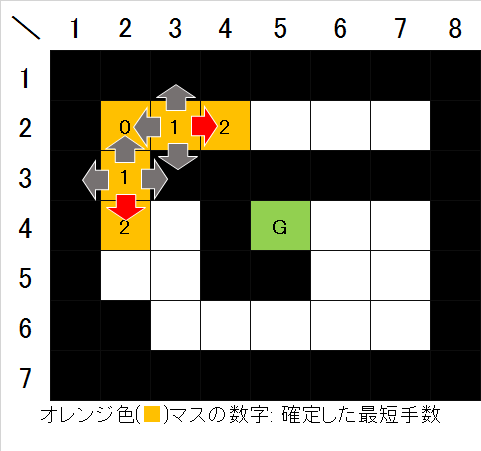図4. 最短手数2でたどり着けるマスが確定- 次に、手数2で確定したそれぞれのマスの4近傍を見て、まだ確定していない空きマスがあればそのマスを手数3で確定させる(図5)。
図5. 最短手数3でたどり着けるマスが確定- 次に、手数3で確定したそれぞれのマスの4近傍を見て、まだ確定していない空きマスがあればそのマスを手数4で確定させる(図6)。
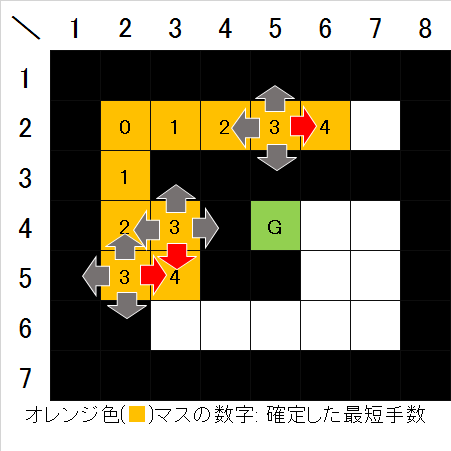図6. 最短手数4でたどり着けるマスが確定- 上記の手順を確定の更新が無くなるまで繰り返すと、スタート地点からたどり着ける全ての空きマスについて最短手数が確定する(図7)。スタートとゴールは必ず空きマスを辿ってたどり着けるという制約があるので、ゴール地点への最短手数も分かる。
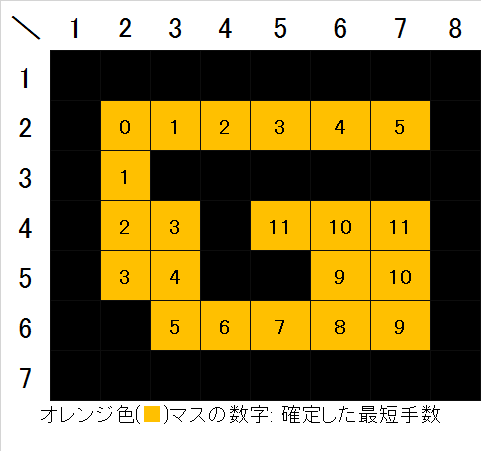図7. すべてのたどり着けるマスへの最短手数が確定さて、この処理をスマートに実装するためには、先入れ先出し(FIFO)のキュー(Queue)というデータ構造を用いると良いことが知られています。もちろん、使わなくても解くことは可能です。今回、よく分からなければ思いついた方法で解くことをおすすめします。先入れ先出しのキューとは以下のような機能を持つデータ構造です。
- 追加(Push): キューの末尾にデータを追加する。
- 取り出し(Pop): キューの先頭のデータを取り出す。
このデータ構造を使うと、先ほどの幅優先探索の説明における「マスの最短手数の確定」のタイミングでその確定マスをキューに追加し、追加操作が終わればPopを行い、取り出したマスの4近傍を調べるということを繰り返せば(つまり先に追加されたものから順番に処理していけば)、簡潔に処理ができることが分かります。
输入格式
入力は以下の形式で標準入力から与えられる。
$ R\ C $
$ sy\ sx $
$ gy\ gx $
$ c_{(1,1)}c_{(1,2)}\ …\ c_{(1,C)} $
$ c_{(2,1)}c_{(2,2)}\ …\ c_{(2,C)} $
:
$ c_{(R,1)}c_{(R,2)}\ …\ c_{(R,C)} $
- 11 行目には、行数 R(1≦R≦50)R(1≦R≦50) と列数 C(1≦C≦50)C(1≦C≦50) がそれぞれ空白区切りで与えられる。
- 22 行目には、スタート地点の座標 (sy,sx)(s**y,s**x) が空白区切りで与えられる。スタート地点が sys**y 行 sxs**x 列にあることを意味する。 1≦sy≦R1≦s**y≦R かつ 1≦sx≦C1≦s**x≦C である。
- 33 行目には、ゴール地点の座標 (gy,gx)(g**y,g**x) が空白区切りで与えられる。ゴール地点が gyg**y 行 gxg**x 列にあることを意味する。 1≦gy≦R1≦g**y≦R かつ 1≦gx≦C1≦g**x≦C であり、 (gy,gx)≠(sy,sx)(g**y,g**x)=(s**y,s**x) であることが保障されている。
- 44 行目から RR 行、長さ CC の文字列が 11 行ずつ与えられる。各文字は
.もしくは#のいずれかであり、 ii 回目 (1≦i≦R)(1≦i≦R) に与えられられる文字列のうち jj 文字目 (1≦j≦C)(1≦j≦C) について、その文字が.なら、マス (i,j)(i,j) が空きマスであり、#なら、マス (i,j)(i,j) が壁マスであることをあらわす。 - 盤面は壁マスで囲まれている。つまり、 i=1,i=R,j=1,j=Ci=1,i=R,j=1,j=C のうちいずれか1つでも条件を満たすマス (i,j)(i,j) について、 c_{(i,j)}c(i,j) は
#である。また、スタート地点とゴール地点は必ず空きマスであり、スタート地点からゴール地点へは、空きマスを辿って必ずたどり着ける。
输出格式
- スタート地点からゴール地点に移動する最小手数を 11 行に出力せよ。最後に改行を忘れないこと。
题意翻译
题面描述：给你一个能上下左右移动的迷宫，求最少需要多少步才能走出迷宫 。
输入格式：第一行两个正整数R，C，分别表示迷宫的行数和列数；
第二行两个正整数sy，sx，表示起点坐标(sy,sx)；
第三行两个正整数gy，gx，表示终点坐标(gy,gx)；
接下来的R行，每行为长度为C的字符串，字符串仅含两种字符，'.'与'#' , '.'表示空地，可以走；'#'表示墙壁，不能走。
输出格式：输出仅一行整数，表示最少需要多少步才能走出迷宫。（题目保证有解）
数据范围：R,C<=50; sy,gy<=R; sx,gx<=C 。
题解：
宽搜基础题目。
其实走地图这种题目，既可以拿宽搜解决，也可以拿深搜解决。但是这道题为什么优先考虑BFS呢？因为BFS的层次性可以方便地求解出最少步数这个信息。
至于宽搜的具体实现，不再赘述。其走向下一步和判断下一步可不可走的部分和深搜一致。只是使用队列这个结构来逐层拓展而已（明明说不赘述然而还是赘述了）
1号裸宽搜代码：
#include<cstdio>
#include<cstring>
#include<queue>
#include<iostream>
using namespace std;
char mp[52][52];
int v[52][52];
int dx[]={0,0,0,-1,1};
int dy[]={0,1,-1,0,0};
int r,c,sx,sy,ex,ey;
struct node
{
int x,y,dep;
}a;
queue<node> q;
int main()
{
int r,c;
scanf("%d%d%d%d%d%d",&r,&c,&sx,&sy,&ex,&ey);
for(int i=1;i<=r;i++)
scanf("%s",mp[i]+1);
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
if(mp[i][j]=='#')
v[i][j]=1;
a.x=sx;a.y=sy;a.dep=0;
q.push(a);
while(!q.empty())
{
node top=q.front();
q.pop();
if(top.x==ex&&top.y==ey)
{
printf("%d\n",top.dep);
break;
}
for(int i=1;i<=4;i++)
{
int xx=top.x+dx[i];
int yy=top.y+dy[i];
if(xx<1||yy<1||xx>r||yy>c||v[xx][yy])
continue;
a.x=xx,a.y=yy,a.dep=top.dep+1;
v[xx][yy]=1;
q.push(a);
}
}
return 0;
}
然后讲一下双向BFS。
双向BFS可以算作是BFS的一种优化。顾名思义就是从两个方向同时开始BFS，碰头即截止 。它适用于既给出起点，又给出终点的情况。非常适合本题。
双向BFS的思路是开两个队列来BFS，每次选取队列长度较小（也就是搜索树规模较小）的那个进行拓展，如果碰头，就直接统计答案。
2号双向BFS代码：
#include<cstdio>
#include<cstring>
#include<queue>
#include<iostream>
using namespace std;
char mp[52][52];
int v1[52][52],v2[52][52];
int ans1[52][52],ans2[52][52];
int dx[]={0,0,0,-1,1};
int dy[]={0,1,-1,0,0};
int r,c,sx,sy,ex,ey;
struct node
{
int x,y;
}a,b;
queue<node> q1;
queue<node> q2;
int main()
{
scanf("%d%d%d%d%d%d",&r,&c,&sx,&sy,&ex,&ey);
if(sx==ex&&sy==ey)
{
puts("0");
return 0;
}
for(int i=1;i<=r;i++)
scanf("%s",mp[i]+1);
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
if(mp[i][j]=='#')
v1[i][j]=v2[i][j]=1;
memset(ans1,127,sizeof(ans1));
memset(ans2,127,sizeof(ans2));
a.x=sx;a.y=sy;
b.x=ex;b.y=ey;
ans1[sx][sy]=0,ans2[ex][ey]=0;
q1.push(a);
q2.push(b);
while(!q1.empty()&&!q2.empty())
{
if(q1.size()<q2.size())
{
node top=q1.front();
q1.pop();
for(int i=1;i<=4;i++)
{
int xx=top.x+dx[i];
int yy=top.y+dy[i];
if(xx<1||yy<1||xx>r||yy>c||v1[xx][yy])
continue;
a.x=xx,a.y=yy;
v1[xx][yy]=1;
ans1[xx][yy]=ans1[top.x][top.y]+1;
q1.push(a);
if(ans2[xx][yy]<=100000)
{
printf("%d\n",ans1[xx][yy]+ans2[xx][yy]);
return 0;
}
}
}
else
{
node top=q2.front();
q2.pop();
for(int i=1;i<=4;i++)
{
int xx=top.x+dx[i];
int yy=top.y+dy[i];
if(xx<1||yy<1||xx>r||yy>c||v2[xx][yy])
continue;
a.x=xx,a.y=yy;
v2[xx][yy]=1;
ans2[xx][yy]=ans2[top.x][top.y]+1;
q2.push(a);
if(ans1[xx][yy]<=100000)
{
printf("%d\n",ans1[xx][yy]+ans2[xx][yy]);
return 0;
}
}
}
}
return 0;
}
