SDOI 2006 保安站岗
SDOI 2006 保安站岗
题目描述
五一来临,某地下超市为了便于疏通和指挥密集的人员和车辆,以免造成超市内的混乱和拥挤,准备临时从外单位调用部分保安来维持交通秩序。
已知整个地下超市的所有通道呈一棵树的形状;某些通道之间可以互相望见。总经理要求所有通道的每个端点(树的顶点)都要有人全天候看守,在不同的通道端点安排保安所需的费用不同。
一个保安一旦站在某个通道的其中一个端点,那么他除了能看守住他所站的那个端点,也能看到这个通道的另一个端点,所以一个保安可能同时能看守住多个端点(树的结点),因此没有必要在每个通道的端点都安排保安。
编程任务:
请你帮助超市经理策划安排,在能看守全部通道端点的前提下,使得花费的经费最少。
输入格式
第1行 n,表示树中结点的数目。
第2行至第n+1行,每行描述每个通道端点的信息,依次为:该结点标号i(0<i<=n),在该结点安置保安所需的经费k(<=10000),该边的儿子数m,接下来m个数,分别是这个节点的m个儿子的标号r1,r2,...,rm。
对于一个n(0 < n <= 1500)个结点的树,结点标号在1到n之间,且标号不重复。
输出格式
最少的经费。
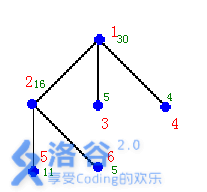
如右图的输入数据示例
输出数据示例:
题解:
小胖守皇宫的双倍经验。一模一样的题,不知道谁抄谁的。
代码:
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1510;
int n,k[maxn],root;
int tot,to[maxn<<1],nxt[maxn<<1],head[maxn];
int dp[maxn][3];
//dp[i][0/1/2]表示i根子树全被覆盖,且i被自己、父亲、儿子覆盖的最小价值。
bool v[maxn];
void add(int x,int y)
{
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs(int x,int f)
{
int son=0;
dp[x][0]=k[x];
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==f)
continue;
dfs(y,x);
dp[x][0]+=min(min(dp[y][0],dp[y][1]),dp[y][2]);
dp[x][1]+=min(dp[y][0],dp[y][2]);
if(!son||dp[son][0]-min(dp[son][0],dp[son][2])>dp[y][0]-min(dp[y][0],dp[y][2]))
son=y;
}
dp[x][2]=dp[son][0];
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==f||y==son)
continue;
dp[x][2]+=min(dp[y][0],dp[y][2]);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int n1,m1;
scanf("%d",&n1);
scanf("%d%d",&k[n1],&m1);
for(int j=1;j<=m1;j++)
{
int x;
scanf("%d",&x);
v[x]=1;
add(x,n1);
add(n1,x);
}
}
for(int i=1;i<=n;i++)
if(!v[i])
{
root=i;
break;
}
dp[0][0]=998244353;
dfs(root,0);
printf("%d",min(dp[root][0],dp[root][2]));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号