详解主席树(可持久化线段树)
详解主席树(可持久化线段树)
本篇随笔详细解读一下算法竞赛中的一种数据结构:主席树。(可持久化线段树)
前置知识当然是线段树,也应该有动态开点。
如果没有掌握请移步:
一、关于可持久化
可持久化数据结构是一个家族,可持久化线段树只是其中的一部分。
关于可持久化数据结构,它的作用是解决“历史版本”的问题。比如,现在的线段树已经经过了\(N\)次修改,但我就是想知道在\(M\)次修改之前的某一个数据是多少。
这就需要可持久化数据结构。可持久化大家族有好多成员,比如可持久化并查集,可持久化树状数组等等...
二、可持久化线段树
那么我们回到刚刚的问题,求一个修改过很多次的线段树的历史版本。
那么,暴力的想法是,每次修改之前,先新开一个线段树,把上个版本的数据复制过去,然后在新树上进行修改,那么,就保留了完整的很多个版本。
你觉得可能么?
我们来打个比方,现在,你抄写了一篇课文。但是里面有些许错字。你当然要去修改这些错字。但是你应该不会选择把整篇文章重抄一遍,因为并不是所有的字都是错的。所以聪明的你选择用涂改带等工具只修改了错字,而保留了大多数正确的字,所以你既节省了效率,又没有因写错字而挨骂。
类比推理可得。
现在,你有一棵线段树,你改了里面的一些东西。但是你应该不会选择把整个树重建一遍,因为有好多节点没有动,你选择把动过的节点新建一遍,其他的节点保留,也达到了建一棵新树的效果。
懂了没有?没懂就看图。
(图片摘自洛谷博客@hyfhaha)
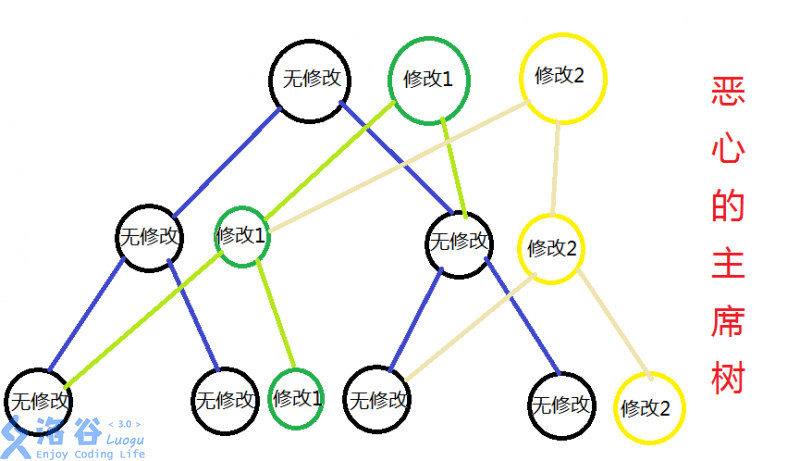
我们发现,所谓可持久化线段树,主席树,就是很多棵非常亲密的线段树(因为有共用节点)。对于一个修改,我们把这个修改影响到的所有节点都新建出来,从叶子节点一直到根。也就是我们只需要新建\(\log N\)个节点,比重构树效率高多了。
经过观察研究,我们很容易发现,
三、可持久化线段树的代码实现
蒟蒻认为这是整个主席树的重点部分。原理很好理解,但是代码实现起来却并不是那么容易,至少细节很多。
我们细细回顾一下主席树的整个过程,我们能够发现,主席树既然是亲密线段树,那么它的节点编号肯定不是普通线段树的那个样子。并且,节点编号我们是无法确定的,因为我们既不知道有多少个版本,也不知道每个版本需要新建多少个节点。所以的话,建树和每次的可持久化修改都需要动态开点,也就是每个节点需要用结构体维护。
1、建树
Code:
struct persistent_segment_tree
{
int val,lson,rson;
}tree[maxn<<2];
//maxn应该是4N+M*log N
int tot;
void build(int &pos,int l,int r)
{
int mid=(l+r)>>1;
if(!pos)
pos=++tot;
if(l==r)
{
tree[pos].val=a[l];
return;
}
build(tree[pos].lson,l,mid);
build(tree[pos].rson,mid+1,r);
tree[pos].val=tree[tree[pos].lson].val+tree[tree[pos].rson].val;
}
因为每次修改只新建了从叶子到根节点的一条路径上的节点,所以每次修改所用的节点个数应该是\(\log N\)级别的,所以最大空间(最多节点数)就应该是\(4N+M\log N\)。
其中,val代表权值,lson/rson代表左右儿子。
然后build函数应该很好理解。
2、可持久化修改
原理见上。现在我们需要选择两个策略:第一种是从下往上修改+新建节点,也就是先找到目标节点,然后向上一层层建新节点;第二种是从上往下修改+新建节点,也就是先建个根出来,然后一层层向下边找边建。
比较容易可得,第一种方式是不行的,因为我们只存了一个节点的左右儿子信息而没有存父亲信息,所以从下往上新建就会”拔剑四顾心茫然“,啥也找不到。
所以我们选择第二种方式,从根节点开始新建,并且开一个root数组来保存版本数,第i个版本的根节点就是root[i],这样的话就能很方便的去查找所有的版本。
Code:
int newnode(int pos)//这里和update函数的返回值都是当前节点在新版本中的新编号是多少
{
tree[++tot]=tree[pos];
return tot;
}
int update(int pos,int l,int r,int x,int k)//将第x个数+k
{
int mid=(l+r)>>1;
pos=newnode(pos);//相当于复制节点,此时节点编号已经变成新节点了,但是维护的信息还没有变,需要后续修改
if(l==r)
{
tree[pos].val+=k;
return pos;
}
if(x<=mid)
tree[pos].lson=update(tree[pos].lson,l,mid,x,k);
else
tree[pos].rson=update(tree[pos].rson,mid+1,r,x,k);
return pos;
}
具体见注释。
3、查询
Code:
int query(int pos,int l,int r,int x)//询问某版本的第x个数,其中初始调用参数为root[i](即表示第i版本)
{
int mid=(l+r)>>1;
if(l==r)
return tree[pos].val;
if(x<=mid)
return query(tree[pos].lson,l,mid,x);
else
return query(tree[pos].rson,mid+1,r,x);
}
那么这道例题洛谷传送门的完整代码就是:
#include<cstdio>
using namespace std;
const int maxn=1e6+10;
int n,m;
int a[maxn],root[maxn];
struct persistent_segment_tree
{
int lson,rson,val;
}tree[maxn*24];
int tot,ver;
void build(int &pos,int l,int r)
{
int mid=(l+r)>>1;
if(!pos)
pos=++tot;
if(l==r)
{
tree[pos].val=a[l];
return;
}
build(tree[pos].lson,l,mid);
build(tree[pos].rson,mid+1,r);
tree[pos].val=tree[tree[pos].lson].val+tree[tree[pos].rson].val;
}
int newnode(int pos)
{
tree[++tot]=tree[pos];
return tot;
}
int update(int pos,int l,int r,int x,int k)
{
int mid=(l+r)>>1;
pos=newnode(pos);
if(l==r)
{
tree[pos].val=k;
return pos;
}
if(x<=mid)
tree[pos].lson=update(tree[pos].lson,l,mid,x,k);
else
tree[pos].rson=update(tree[pos].rson,mid+1,r,x,k);
return pos;
}
int query(int pos,int l,int r,int x)
{
int mid=(l+r)>>1;
if(l==r)
return tree[pos].val;
if(x<=mid)
return query(tree[pos].lson,l,mid,x);
else
return query(tree[pos].rson,mid+1,r,x);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build(root[0],1,n);
while(m--)
{
int v,opt;
int x,k;
scanf("%d%d",&v,&opt);
if(opt==1)
{
scanf("%d%d",&x,&k);
root[++ver]=update(root[v],1,n,x,k);
}
else
{
scanf("%d",&x);
root[++ver]=root[v];
printf("%d\n",query(root[v],1,n,x));
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号