浅谈换根DP
浅谈换根DP
本篇随笔浅谈一下算法竞赛中的换根DP。
换根DP概念
换根DP其实是树形DP的一种延伸技巧或者说是方法。
它的使用范围是，对树上的每个点跑树形DP。这样的话，不用换根DP一点一点跑的复杂度就是\(O(n^2)\)，必炸。那么换根DP应运而生。简单来讲，就是我们会通过推理发现，我们先以一个选定节点跑出来的最优解，通过另一个转移方程，就可以得出与他有关系的其他节点的答案。也就是说，我们相当于进行了两次DP，第一次的树形DP可以算作一种预处理，第二次的DP就是换根DP。其根本奥义就是用\(O(2N)\)的复杂度完成了\(O(N^2)\)的问题。
换根DP例题
POJ 3585
让我们用一道例题来更深理解换根DP~
题目大意：
有一棵有\(n\)个节点、\(n-1\)条边的无根树，每边有一流量限制。令某一节点为根节点，向根节点灌水，最终从叶子节点流出的水量和为这一节点的最大流量。问：在做根节点的所有节点中，最大的最大流量是多少？
题解：
很容易想到这个某个节点的最大流量可以用树形DP来维护，但是因为一次树形DP是\(O(n)\)的复杂度，如果有\(n\)个点，那么其复杂度就是\(O(n^2)\)的，\(n\le 2*10^5\)，还是多组数据，必炸无疑。
那么就不能暴力地在每个节点都跑一次树形DP，即需要一种不需要每次都跑的船新操作。
我们叫他换根DP。我的理解就是，树形DP+换根。
俗称扭一扭，因为在换根的过程中，树的形态发生了扭转。
那么我们考虑，用一次树形DP作为信息的预处理，然后之后的答案能否通过预处理，使用换根DP来维护呢？
PS：先讲树形DP预处理。
一般来讲，树的形态固定的情况下，才可以把边权转点权（把边权值给儿子，比如树链剖分等等，比较常见的操作）。但换根DP因为树的形态会扭，所以不适合把边权转点券。那么我们DP设置的状态就需要以边作维护。
状态设置为：\(sum[x]\)表示以\(x\)点为根的子树所能提供的最大流量和，那么显然，儿子节点对于父亲的贡献就是这个\(sum[x]\)和父亲到儿子的边权的较小值。比如下图（以1为根），\(sum[4]=15\)，但是\(4\)号点对答案的贡献其实是13，因为被限制了。
所以转移方程就是：
需要注意的是初值，叶子节点的\(sum\)值应该为0，所以转移的时候应该从倒数第二层节点开始转，这个处理我们可以通过特判解决。
于是我们处理出了一个以\(1\)为根的\(sum\)数组，答案就是\(sum[1]\)。
然后就是扭一扭的过程，先上图。
比如，以1为根的情况和以4为根的情况：（如图）
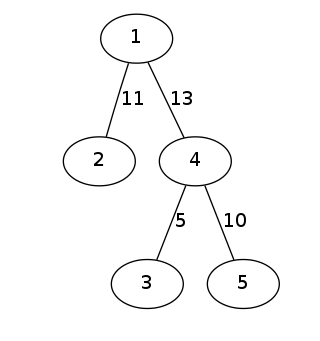
我们发现，4-3-5这棵子树的信息是没有变化的，只是原先1是4的儿子，现在儿子翻身当爹了而已，也就是，只有以1为根的子树的信息需要重新统计。我们又发现，1有很多儿子，其中只有4当了爹，其他的儿子依然是儿子，所以只需要把1之前与4的关系断掉，进行重新统计。也就是说，原来的\(sum[1]\)要减去\(sum[4]\)和它俩之间的边权的较小值，也就是13。成为新的\(sum[1]\)。
然后在新的根节点4上加上新的\(sum[1]\)即可。
这个扭一扭的过程可以通过第二次深搜来实现。
需要注意的细节是，当我们进行到叶子节点的时候，需要进行特殊判断，很容易得出，在叶子节点和非叶子节点的转移方程是不一样的。
详见代码：
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=2*1e5+10;
int n;
int tot,to[maxn<<1],nxt[maxn<<1],val[maxn<<1],head[maxn];
int sum[maxn<<1],dp[maxn<<1],du[maxn],ans;
void add(int x,int y,int z)
{
to[++tot]=y;
val[tot]=z;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs1(int x,int f)
{
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==f)
continue;
dfs1(y,x);
if(du[y]>1)
sum[x]+=min(val[i],sum[y]);
else
sum[x]+=val[i];
}
}
void dfs2(int x,int f)
{
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==f)
continue;
if(du[x]==1)//leaf
dp[y]=sum[y]+val[i];
else
dp[y]=sum[y]+min(dp[x]-min(sum[y],val[i]),val[i]);
dfs2(y,x);
}
}
void clean()
{
tot=0;
ans=-1;
memset(sum,0,sizeof(sum));
memset(du,0,sizeof(du));
memset(dp,0,sizeof(dp));
memset(to,0,sizeof(to));
memset(nxt,0,sizeof(nxt));
memset(head,0,sizeof(head));
memset(val,0,sizeof(val));
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
clean();
scanf("%d",&n);
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
du[x]++;
du[y]++;
}
dfs1(1,0);
dp[1]=sum[1];
dfs2(1,0);
for(int i=1;i<=n;i++)
ans=max(ans,dp[i]);
printf("%d\n",ans);
}
return 0;
}
这就是换根DP啦~
